北师大版九年级上册数学 3.1.1用树状图或表格求简单事件的概率 课件(共31张PPT)
文档属性
| 名称 | 北师大版九年级上册数学 3.1.1用树状图或表格求简单事件的概率 课件(共31张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-22 15:30:51 | ||
图片预览










文档简介
(共31张PPT)
用树状图与列表法求概率
为了坚持计划生育基本国策,应对人口老龄化趋势,2015年10月中国共产党十八届五中全会公报允许普遍二孩即全面开放二胎,即一对夫妻可以生两个孩子。
2016年1月1日,我国正式实施全面二胎政策。
问题:
一对夫妻生一个孩子的可能性有哪几种?生男孩的可能性是多少?
一对夫妻生两个孩子又有哪几种可能?
恰好一男一女的可能性是多少?
频率与概率知几何
回顾与思考
概率 事件发生的可能性,也称为事件发生的概率(probability).
必然事件发生的概率为1(或100%),记作P(必然事件)=1;
不可能事件发生的概率为0,记作P(不可能事件)=0;
不确定事件发生的概率介于0~1之间, 即 0如果A为不确定事件,那么0概率
引 入
小明、小颖和小凡都想去看周末电影,但只有一张电影票,三人决定一起做游戏,谁获胜谁就去看电影,游戏规则如下:
问题源于生活
连续掷两枚质地均匀的硬币,若两枚正面朝上,则小明获胜,若两枚反面朝上,则小颖获胜,若一枚正面朝上,一枚反面朝上,则小凡获胜。你认为这个游戏公平吗?
做一做
问题源于生活
连续掷两枚质地均匀的硬币,“两枚正面朝上”,“两枚反面朝上”,“一枚正面朝上,一枚反面朝上”,这三个事件发生的概率相同吗?
先分组进行试验,然后累计各组的实验数据,分别计算这三个事件发生的频数与频率,并由此估计相应的概率?
做一做
问题源于生活
通过大量的重复试验我们发现:在一般情况下, “一枚正面朝上,一枚反面朝上”发生的概率大于其他两个事件发生的概率。所以,这个游戏不公平,对小凡比较有利。
实际上:我们可以用树状图或表格来研究上述问题
开始
第一枚硬币
正
反
第二枚硬币
正
反
正
反
所有可能出现的结果
(正,正)
问题探究
(正,反)
(反,正)
(反,反)
“悟”的功效
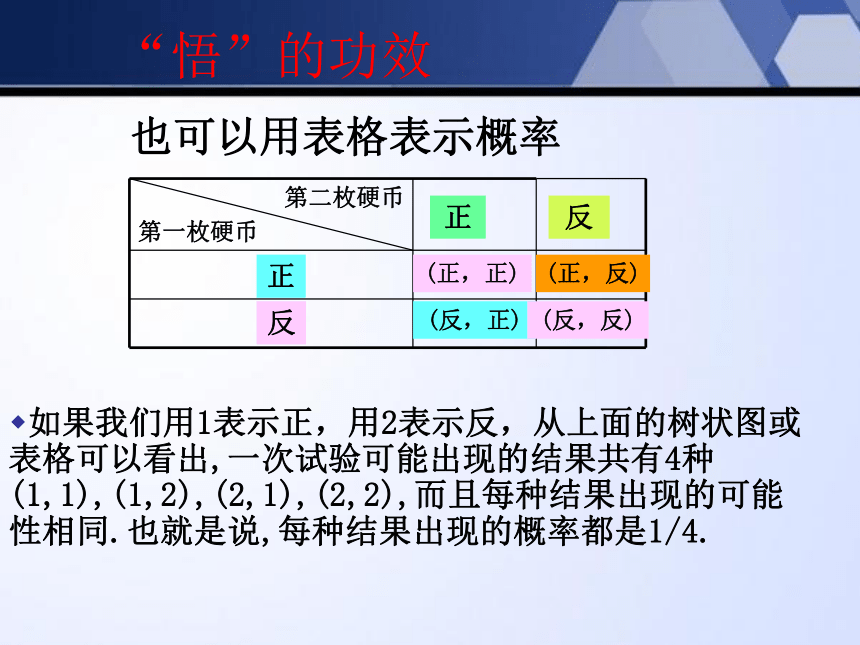
如果我们用1表示正,用2表示反,从上面的树状图或 表格可以看出,一次试验可能出现的结果共有4种(1,1),(1,2),(2,1),(2,2),而且每种结果出现的可能性相同.也就是说,每种结果出现的概率都是1/4.
也可以用表格表示概率
第二枚硬币
第一枚硬币
正
正
反
(正,正)
(正,反)
反
(反,正)
(反,反)
在上面投掷硬币的实验中。
“悟”的功效
议一议
(1),投掷第一枚硬币可能出现哪些结果?他们发生的可能性是否一样?
答:一正一反 一样
(2),投掷第二枚硬币可能出现哪些结果?他们发生的可能性是否一样?
答:一正一反 一样
在上面投掷硬币的实验中。
“悟”的功效
议一议
利用树状图或表格,可以比较方便地求出某些事件发生的概率.
(3),在第一枚硬币正面朝上的情况下,第二枚硬币可能出现哪些结果?他们发生的可能性是否一样?如果第一枚硬币反面朝上呢?
答:一正一反 一样
答:一正一反 一样
行家看“门道”
例题欣赏
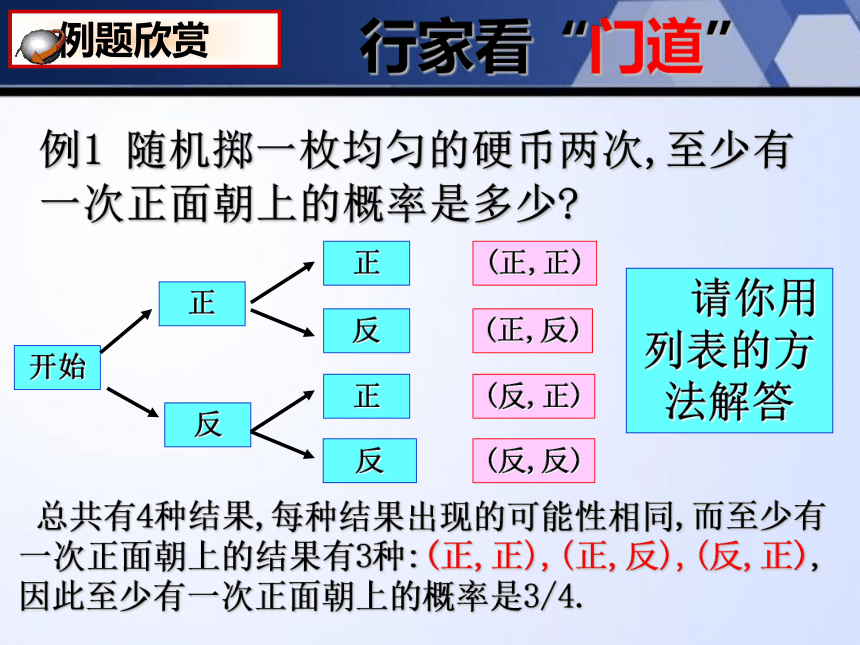
例1 随机掷一枚均匀的硬币两次,至少有一次正面朝上的概率是多少
总共有4种结果,每种结果出现的可能性相同,而至少有一次正面朝上的结果有3种:(正,正),(正,反),(反,正),因此至少有一次正面朝上的概率是3/4.
开始
正
反
正
反
正
反
(正,正)
(正,反)
(反,正)
(反,反)
请你用列表的方法解答
第二枚硬币
第一枚硬币
(正,正)
(正,反)
(反,正)
(反,反)
第二种方法:列表法
总共有4种结果,每种结果出现的可能性相同,而至少有一次正面朝上的结果有3种:(正,正)(正,反)(反,正),因此至少有一次正面朝上的概率为3/4。
本节开始的问题解答:
总共有4种结果,每种结果出现的可能性相同,其中
因此这个游戏对三人是不公平的,这个游戏对小凡有利
小明获胜的结果有一种:(正,正),所以小明获胜的概率为1/4.
小颖获胜的结果有一种:(反,反),所以小颖获胜的概率为1/4.
小凡获胜的结果有两种:(正,反),(反,正),所以小凡获胜的概率为2/4.
利用树状图或者表格,我们可以不重复、不遗漏的列出所有可能的结果,从而比较方便地求出某些事件发生的概率。
问题:
一对夫妻生一个孩子的可能性有哪几种?生男孩的可能性是多少?
一对夫妻生两个孩子又有哪几种可能?恰好一男一女的可能性是多少?
随堂练习
小颖有两件上衣,分别为红色和白色,有两条裤子,分别为黑色和白色,她随机拿出一件上衣和一条裤子穿上,恰好是白色上衣和白色裤子的概率是多少?
上衣\裤子 黑裤子 白裤子
红上衣 (红,黑) (红,白)
白上衣 (白,黑) (白,白)
解:用列表的方法可得。
答:总共有四种结果,每种结果出现的可能性相同,因此。恰好是白色上衣和白色裤子的概率是1/4?
小明、小颖和小凡做“石头、剪子、布”的游戏。游戏规则如下:有小明和小颖做“石头、剪子、布”的游戏如果两人的手势相同,那么小凡获胜;如果两人手势不同,那么按照“石头胜剪子,剪子胜布,布胜石头”的规则决定小明和小颖中的获胜者。
用树状图或表格求概率 P62
温故知新
上节课,你学会了用什么方法求某个事件发生的概率
树状图和列表法
问题提出
小明、小颖和小凡做“石头、剪刀、布”的游戏,游戏规则如下:
由小明和小颖玩“石头、剪刀、布”游戏,如果两人的手势相同,那么小凡获胜;如果两人手势不同,那么按照“石头胜剪刀,剪刀胜布,布胜石头”的规则决定小明和小颖中的获胜者.
假设小明和小颖每次出这三种手势的可能性相同,你认为这个游戏对三人公平吗?
解:因为小明和小颖每次出这三种手势的可能性相同,所以可利用树状图列出所有可能出现的结果:
石头
剪刀
布
石头
剪刀
布
小明
开始
剪刀
石头
布
石头
剪刀
布
小颖
(石头,石头)
(石头,剪刀)
(石头,布)
(剪刀,石头)
(剪刀,剪刀)
(剪刀,布)
(布,石头)
(布,剪刀)
(布,布)
所有可能出现的结果
总共有9种可能的结果,每种结果出现的可能性相同,而两人手势相同的结果有三种:(石头,石头)(剪刀,剪刀)(布,布),所以小凡获胜的概率为
小明胜小颖的结果有三种:(石头,剪刀)(剪刀,布)(布,石头),所以小明获胜的概率为
小颖胜小明的结果也有三种:(剪刀,石头)(布,剪刀)(石头,布),所以小颖获胜的概率为
所以,这个游戏对三人是公平的.
你能用列表的方法求出来吗?
用树状图或表格求概率 P62
答:用列表的方法如下.
1.准备两组相同的牌,每组三张且大小一样,三张牌的牌面数字分别是1,2,3,从每组牌中各摸出一张牌。
习题讲解 P64
(1)两张牌的牌面数字和等于1的概率是多少?
(2)两张牌的牌面数字和等于2的概率是多少?
(3)两张牌的牌面数字和为几的概率最大?
(4)两张牌的牌面数字和大于3的概率是多少?
开始
第一张牌的牌面的数字
1
3
第二张牌的牌面的数字
1
3
2
3
所有可能
出现的结果
(1,1)
(1,2)
(1,3)
(2,1)
2
2
1
1
3
2
(2,3)
(3,1)
(3,2)
(3,3)
(2,2)
树
状
图
第二张牌的牌面数字
第一张牌的牌面数字
1
1
2
(1,1)
(1,2)
2
(2,1)
(2,2)
3
3
(1,3)
(2,3)
(3,1)
(3,2)
(3,3)
表
格
由上可得:
习题讲解 P64
(1)两张牌的牌面数字和等于1的概率是0.
(2)两张牌的牌面数字和等于2的概率是1/9.
(3)两张牌的牌面数字和为4的概率最大.
(4)两张牌的牌面数字和大于3的概率是2/3.
2.经过某路口的行人,可能直行,也可能左拐或右拐,假设这三种可能性相同,现有两人经过该路口,求下列事件的概率。
习题讲解 P64
(1)两人都左拐;
(2)恰好有一人直行,另一人左拐;
(3)至少有一人直行。
答:(1)1/9;(2)2/9;(3)5/9.
3.掷两枚质地均匀的骰子,求下列事件的概率。
习题讲解 P64
(1)至少有一枚骰子的点数为1;
(2)两枚骰子的点数和为奇数;
(3)两枚骰子的点数和大于9;
(4)第二枚骰子的点数整除第一枚骰子的点数。
4.小明何小军做掷骰子游戏,两人各掷一枚质地均匀的骰子。
习题讲解 P64
(1)若两人掷得的点数之和为奇数,则小军获胜,否则小明获胜。这个游戏对双方公平吗?为什么?;
答:共有36种结果。和为奇数的有18种,两人获胜的概率都是1/2,因此,公平。
4.小明何小军做掷骰子游戏,两人各掷一枚质地均匀的骰子。
习题讲解 P64
答:共有36种结果。积为奇数的有9种,小军获胜的概率都是1/4,因此,不公平。
(2)若两人掷得的点数之积为奇数,则小军获胜,否则小明获胜。这个游戏对双方公平吗?为什么?;
5.续上解:所有可能的结果
.
在玩中学数学,用数学习题3.2P65
因此:所有可能的结果有36种,点数和为7的有6种,小红下一次得到“汽车”的概率为6/36,即1/6.
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;从而较方便地求出某些事件发生的概率.
用树状图或表格来求概率
回顾与思考
用树状图与列表法求概率
为了坚持计划生育基本国策,应对人口老龄化趋势,2015年10月中国共产党十八届五中全会公报允许普遍二孩即全面开放二胎,即一对夫妻可以生两个孩子。
2016年1月1日,我国正式实施全面二胎政策。
问题:
一对夫妻生一个孩子的可能性有哪几种?生男孩的可能性是多少?
一对夫妻生两个孩子又有哪几种可能?
恰好一男一女的可能性是多少?
频率与概率知几何
回顾与思考
概率 事件发生的可能性,也称为事件发生的概率(probability).
必然事件发生的概率为1(或100%),记作P(必然事件)=1;
不可能事件发生的概率为0,记作P(不可能事件)=0;
不确定事件发生的概率介于0~1之间, 即 0
引 入
小明、小颖和小凡都想去看周末电影,但只有一张电影票,三人决定一起做游戏,谁获胜谁就去看电影,游戏规则如下:
问题源于生活
连续掷两枚质地均匀的硬币,若两枚正面朝上,则小明获胜,若两枚反面朝上,则小颖获胜,若一枚正面朝上,一枚反面朝上,则小凡获胜。你认为这个游戏公平吗?
做一做
问题源于生活
连续掷两枚质地均匀的硬币,“两枚正面朝上”,“两枚反面朝上”,“一枚正面朝上,一枚反面朝上”,这三个事件发生的概率相同吗?
先分组进行试验,然后累计各组的实验数据,分别计算这三个事件发生的频数与频率,并由此估计相应的概率?
做一做
问题源于生活
通过大量的重复试验我们发现:在一般情况下, “一枚正面朝上,一枚反面朝上”发生的概率大于其他两个事件发生的概率。所以,这个游戏不公平,对小凡比较有利。
实际上:我们可以用树状图或表格来研究上述问题
开始
第一枚硬币
正
反
第二枚硬币
正
反
正
反
所有可能出现的结果
(正,正)
问题探究
(正,反)
(反,正)
(反,反)
“悟”的功效
如果我们用1表示正,用2表示反,从上面的树状图或 表格可以看出,一次试验可能出现的结果共有4种(1,1),(1,2),(2,1),(2,2),而且每种结果出现的可能性相同.也就是说,每种结果出现的概率都是1/4.
也可以用表格表示概率
第二枚硬币
第一枚硬币
正
正
反
(正,正)
(正,反)
反
(反,正)
(反,反)
在上面投掷硬币的实验中。
“悟”的功效
议一议
(1),投掷第一枚硬币可能出现哪些结果?他们发生的可能性是否一样?
答:一正一反 一样
(2),投掷第二枚硬币可能出现哪些结果?他们发生的可能性是否一样?
答:一正一反 一样
在上面投掷硬币的实验中。
“悟”的功效
议一议
利用树状图或表格,可以比较方便地求出某些事件发生的概率.
(3),在第一枚硬币正面朝上的情况下,第二枚硬币可能出现哪些结果?他们发生的可能性是否一样?如果第一枚硬币反面朝上呢?
答:一正一反 一样
答:一正一反 一样
行家看“门道”
例题欣赏
例1 随机掷一枚均匀的硬币两次,至少有一次正面朝上的概率是多少
总共有4种结果,每种结果出现的可能性相同,而至少有一次正面朝上的结果有3种:(正,正),(正,反),(反,正),因此至少有一次正面朝上的概率是3/4.
开始
正
反
正
反
正
反
(正,正)
(正,反)
(反,正)
(反,反)
请你用列表的方法解答
第二枚硬币
第一枚硬币
(正,正)
(正,反)
(反,正)
(反,反)
第二种方法:列表法
总共有4种结果,每种结果出现的可能性相同,而至少有一次正面朝上的结果有3种:(正,正)(正,反)(反,正),因此至少有一次正面朝上的概率为3/4。
本节开始的问题解答:
总共有4种结果,每种结果出现的可能性相同,其中
因此这个游戏对三人是不公平的,这个游戏对小凡有利
小明获胜的结果有一种:(正,正),所以小明获胜的概率为1/4.
小颖获胜的结果有一种:(反,反),所以小颖获胜的概率为1/4.
小凡获胜的结果有两种:(正,反),(反,正),所以小凡获胜的概率为2/4.
利用树状图或者表格,我们可以不重复、不遗漏的列出所有可能的结果,从而比较方便地求出某些事件发生的概率。
问题:
一对夫妻生一个孩子的可能性有哪几种?生男孩的可能性是多少?
一对夫妻生两个孩子又有哪几种可能?恰好一男一女的可能性是多少?
随堂练习
小颖有两件上衣,分别为红色和白色,有两条裤子,分别为黑色和白色,她随机拿出一件上衣和一条裤子穿上,恰好是白色上衣和白色裤子的概率是多少?
上衣\裤子 黑裤子 白裤子
红上衣 (红,黑) (红,白)
白上衣 (白,黑) (白,白)
解:用列表的方法可得。
答:总共有四种结果,每种结果出现的可能性相同,因此。恰好是白色上衣和白色裤子的概率是1/4?
小明、小颖和小凡做“石头、剪子、布”的游戏。游戏规则如下:有小明和小颖做“石头、剪子、布”的游戏如果两人的手势相同,那么小凡获胜;如果两人手势不同,那么按照“石头胜剪子,剪子胜布,布胜石头”的规则决定小明和小颖中的获胜者。
用树状图或表格求概率 P62
温故知新
上节课,你学会了用什么方法求某个事件发生的概率
树状图和列表法
问题提出
小明、小颖和小凡做“石头、剪刀、布”的游戏,游戏规则如下:
由小明和小颖玩“石头、剪刀、布”游戏,如果两人的手势相同,那么小凡获胜;如果两人手势不同,那么按照“石头胜剪刀,剪刀胜布,布胜石头”的规则决定小明和小颖中的获胜者.
假设小明和小颖每次出这三种手势的可能性相同,你认为这个游戏对三人公平吗?
解:因为小明和小颖每次出这三种手势的可能性相同,所以可利用树状图列出所有可能出现的结果:
石头
剪刀
布
石头
剪刀
布
小明
开始
剪刀
石头
布
石头
剪刀
布
小颖
(石头,石头)
(石头,剪刀)
(石头,布)
(剪刀,石头)
(剪刀,剪刀)
(剪刀,布)
(布,石头)
(布,剪刀)
(布,布)
所有可能出现的结果
总共有9种可能的结果,每种结果出现的可能性相同,而两人手势相同的结果有三种:(石头,石头)(剪刀,剪刀)(布,布),所以小凡获胜的概率为
小明胜小颖的结果有三种:(石头,剪刀)(剪刀,布)(布,石头),所以小明获胜的概率为
小颖胜小明的结果也有三种:(剪刀,石头)(布,剪刀)(石头,布),所以小颖获胜的概率为
所以,这个游戏对三人是公平的.
你能用列表的方法求出来吗?
用树状图或表格求概率 P62
答:用列表的方法如下.
1.准备两组相同的牌,每组三张且大小一样,三张牌的牌面数字分别是1,2,3,从每组牌中各摸出一张牌。
习题讲解 P64
(1)两张牌的牌面数字和等于1的概率是多少?
(2)两张牌的牌面数字和等于2的概率是多少?
(3)两张牌的牌面数字和为几的概率最大?
(4)两张牌的牌面数字和大于3的概率是多少?
开始
第一张牌的牌面的数字
1
3
第二张牌的牌面的数字
1
3
2
3
所有可能
出现的结果
(1,1)
(1,2)
(1,3)
(2,1)
2
2
1
1
3
2
(2,3)
(3,1)
(3,2)
(3,3)
(2,2)
树
状
图
第二张牌的牌面数字
第一张牌的牌面数字
1
1
2
(1,1)
(1,2)
2
(2,1)
(2,2)
3
3
(1,3)
(2,3)
(3,1)
(3,2)
(3,3)
表
格
由上可得:
习题讲解 P64
(1)两张牌的牌面数字和等于1的概率是0.
(2)两张牌的牌面数字和等于2的概率是1/9.
(3)两张牌的牌面数字和为4的概率最大.
(4)两张牌的牌面数字和大于3的概率是2/3.
2.经过某路口的行人,可能直行,也可能左拐或右拐,假设这三种可能性相同,现有两人经过该路口,求下列事件的概率。
习题讲解 P64
(1)两人都左拐;
(2)恰好有一人直行,另一人左拐;
(3)至少有一人直行。
答:(1)1/9;(2)2/9;(3)5/9.
3.掷两枚质地均匀的骰子,求下列事件的概率。
习题讲解 P64
(1)至少有一枚骰子的点数为1;
(2)两枚骰子的点数和为奇数;
(3)两枚骰子的点数和大于9;
(4)第二枚骰子的点数整除第一枚骰子的点数。
4.小明何小军做掷骰子游戏,两人各掷一枚质地均匀的骰子。
习题讲解 P64
(1)若两人掷得的点数之和为奇数,则小军获胜,否则小明获胜。这个游戏对双方公平吗?为什么?;
答:共有36种结果。和为奇数的有18种,两人获胜的概率都是1/2,因此,公平。
4.小明何小军做掷骰子游戏,两人各掷一枚质地均匀的骰子。
习题讲解 P64
答:共有36种结果。积为奇数的有9种,小军获胜的概率都是1/4,因此,不公平。
(2)若两人掷得的点数之积为奇数,则小军获胜,否则小明获胜。这个游戏对双方公平吗?为什么?;
5.续上解:所有可能的结果
.
在玩中学数学,用数学习题3.2P65
因此:所有可能的结果有36种,点数和为7的有6种,小红下一次得到“汽车”的概率为6/36,即1/6.
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;从而较方便地求出某些事件发生的概率.
用树状图或表格来求概率
回顾与思考
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
