五年级上册数学苏教版 图形与几何专题教材分析 课件 (共13张PPT)
文档属性
| 名称 | 五年级上册数学苏教版 图形与几何专题教材分析 课件 (共13张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-22 19:14:07 | ||
图片预览



文档简介
(共13张PPT)
苏教版数学五年级上册教材分析及教学建议
图形与几何专题
第二单元 多边形的面积
教学内容:
第一段 平行四边形、三角形的面积,例1~例5和练习二。
第二段 梯形的面积,公顷和平方千米,例6、例7、例8和练习三。
第三段 简单组合图形和不规则图形的面积,例10例11和练习四。
还安排了实践与综合“校园的绿地面积”,综合应用各种图形的面积公式,解决一些稍复杂图形的面积计算问题,进一步体会这部分内容在实际生活中的应用价值。
教学重点:探索并掌握平行四边形、三角形的面积公式
教学难点:不规则图形面积的估计。
理解几种图形面积计算公式之间的联系和区别,灵活解决问题。
图形与几何
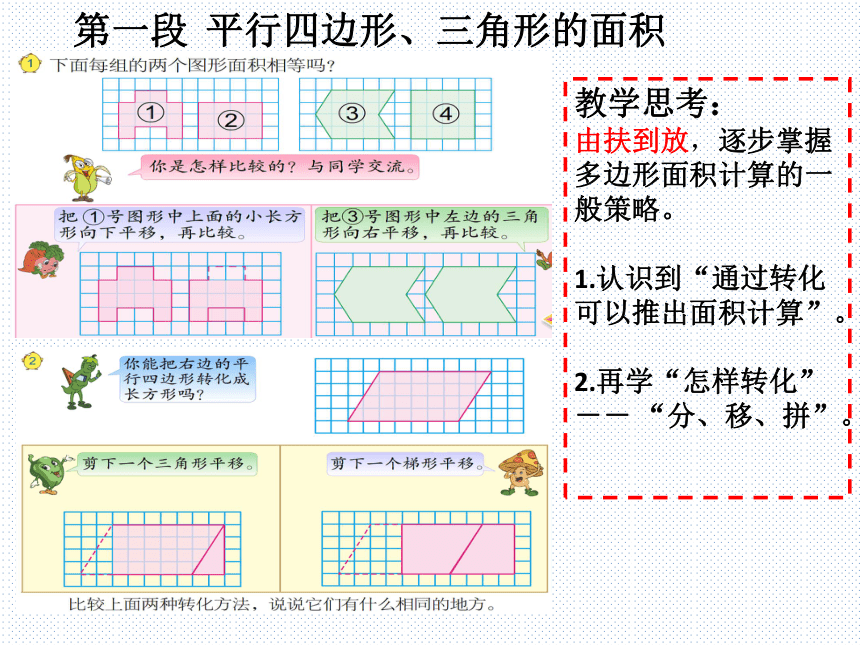
第一段 平行四边形、三角形的面积
教学思考:
由扶到放,逐步掌握多边形面积计算的一般策略。
1.认识到“通过转化可以推出面积计算”。
2.再学“怎样转化”-- “分、移、拼”。
教学关键:
研究平行四边形与转化成的长方形之间的联系。
1.操作、体会:
任意平行四边形都能转化成长方形。
2.分析数据、建立猜想:平行四边形的面积可能是底与高的乘积。
3.讨论推理,验证猜想。
4.获得结论。
长方形的面积 =长×宽
平行四边形的面积=底×高
平行四边形的面积
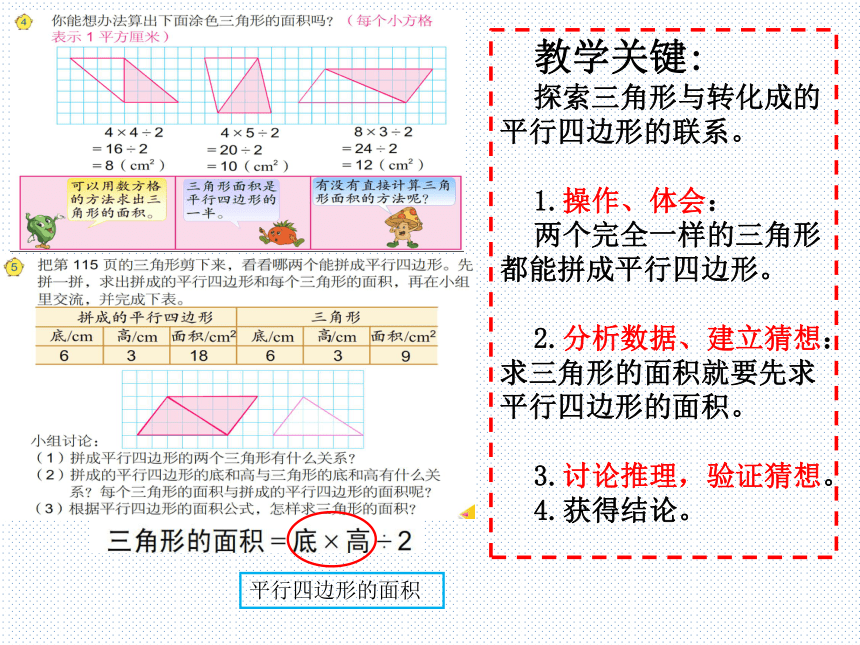
教学关键:
探索三角形与转化成的平行四边形的联系。
1.操作、体会:
两个完全一样的三角形都能拼成平行四边形。
2.分析数据、建立猜想:求三角形的面积就要先求平行四边形的面积。
3.讨论推理,验证猜想。
4.获得结论。
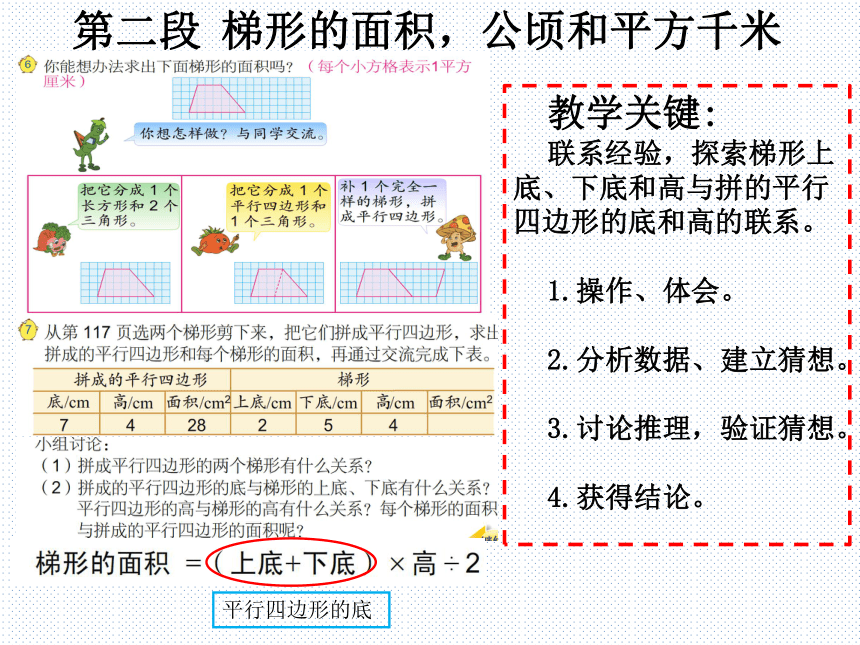
第二段 梯形的面积,公顷和平方千米
平行四边形的底
教学关键:
联系经验,探索梯形上底、下底和高与拼的平行四边形的底和高的联系。
1.操作、体会。
2.分析数据、建立猜想。
3.讨论推理,验证猜想。
4.获得结论。
多边形面积计算的推导
教学思考:
把认识概念和探索相关单位之间的进率结合起来。
1.情境引出“公顷”,产生学习需求。
2.认识1公顷的含义,推算1公顷等于10000平方米。
3.在实践中推想、感受1公顷的大小。
1.情境引出“平方千米”,产生学习需求。
2.认识1平方千米的含义。
3.探索平方千米与平方米、公顷之间的进率,学会进行简单的换算。
4.适时回忆并整理学过的面积单位。
第三段 简单组合图形,不规则图形的面积
教学关键:
1.形成解题思路:把组合图形转化成几个(尽量少)基本图形。
2.推想必要的数据,耐心计算。
3.形成解题策略: “分割”求“和”,“拼补”求“差”。
整格:55格,半格:36格
第一种:55+36=91(公顷)
答:湖泊面积大约在55~91公顷之间。
第二种:36÷2=18(公顷)
55+18=73(公顷)
答:湖泊面积大约是73公顷。
教学关键:
1.理解多种估计方法的特点。
2.比较不同的估计方法,体会确定上、下界对于面积估计意义和价值。
教学关键:
重视实际测量方法的指导,感受多边形面积计算的应用价值,提高解决问题的能力。
1.明确分工,有人负责测量,有人负责记录。
2.要选择合适的、便于测量的地块。
3.选择合适的测量工具,通常可选择卷尺或米尺。
4.具体指导图形高的测量方法。
5.适当地取近似值,以便于计算。
谢 谢
苏教版数学五年级上册教材分析及教学建议
图形与几何专题
第二单元 多边形的面积
教学内容:
第一段 平行四边形、三角形的面积,例1~例5和练习二。
第二段 梯形的面积,公顷和平方千米,例6、例7、例8和练习三。
第三段 简单组合图形和不规则图形的面积,例10例11和练习四。
还安排了实践与综合“校园的绿地面积”,综合应用各种图形的面积公式,解决一些稍复杂图形的面积计算问题,进一步体会这部分内容在实际生活中的应用价值。
教学重点:探索并掌握平行四边形、三角形的面积公式
教学难点:不规则图形面积的估计。
理解几种图形面积计算公式之间的联系和区别,灵活解决问题。
图形与几何
第一段 平行四边形、三角形的面积
教学思考:
由扶到放,逐步掌握多边形面积计算的一般策略。
1.认识到“通过转化可以推出面积计算”。
2.再学“怎样转化”-- “分、移、拼”。
教学关键:
研究平行四边形与转化成的长方形之间的联系。
1.操作、体会:
任意平行四边形都能转化成长方形。
2.分析数据、建立猜想:平行四边形的面积可能是底与高的乘积。
3.讨论推理,验证猜想。
4.获得结论。
长方形的面积 =长×宽
平行四边形的面积=底×高
平行四边形的面积
教学关键:
探索三角形与转化成的平行四边形的联系。
1.操作、体会:
两个完全一样的三角形都能拼成平行四边形。
2.分析数据、建立猜想:求三角形的面积就要先求平行四边形的面积。
3.讨论推理,验证猜想。
4.获得结论。
第二段 梯形的面积,公顷和平方千米
平行四边形的底
教学关键:
联系经验,探索梯形上底、下底和高与拼的平行四边形的底和高的联系。
1.操作、体会。
2.分析数据、建立猜想。
3.讨论推理,验证猜想。
4.获得结论。
多边形面积计算的推导
教学思考:
把认识概念和探索相关单位之间的进率结合起来。
1.情境引出“公顷”,产生学习需求。
2.认识1公顷的含义,推算1公顷等于10000平方米。
3.在实践中推想、感受1公顷的大小。
1.情境引出“平方千米”,产生学习需求。
2.认识1平方千米的含义。
3.探索平方千米与平方米、公顷之间的进率,学会进行简单的换算。
4.适时回忆并整理学过的面积单位。
第三段 简单组合图形,不规则图形的面积
教学关键:
1.形成解题思路:把组合图形转化成几个(尽量少)基本图形。
2.推想必要的数据,耐心计算。
3.形成解题策略: “分割”求“和”,“拼补”求“差”。
整格:55格,半格:36格
第一种:55+36=91(公顷)
答:湖泊面积大约在55~91公顷之间。
第二种:36÷2=18(公顷)
55+18=73(公顷)
答:湖泊面积大约是73公顷。
教学关键:
1.理解多种估计方法的特点。
2.比较不同的估计方法,体会确定上、下界对于面积估计意义和价值。
教学关键:
重视实际测量方法的指导,感受多边形面积计算的应用价值,提高解决问题的能力。
1.明确分工,有人负责测量,有人负责记录。
2.要选择合适的、便于测量的地块。
3.选择合适的测量工具,通常可选择卷尺或米尺。
4.具体指导图形高的测量方法。
5.适当地取近似值,以便于计算。
谢 谢
同课章节目录
