空间几何体的体积课件
图片预览







文档简介
课件42张PPT。在数学这门学科里,我们发现真理的主要工具是归纳和类比。
——拉普拉斯数学中的一些美丽定理具有这样的特性:它们极易从事实中归纳出来,但证明却隐藏得极深。
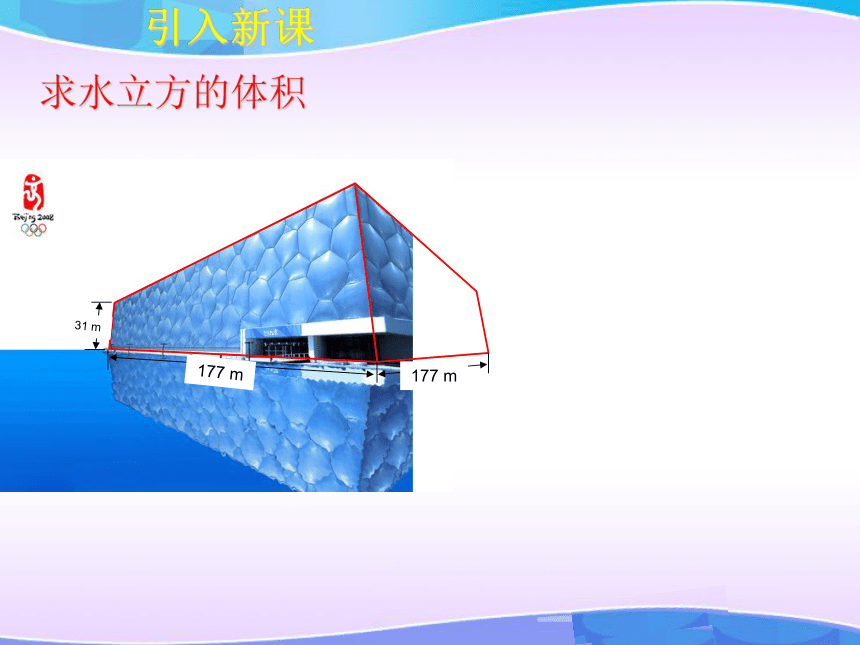
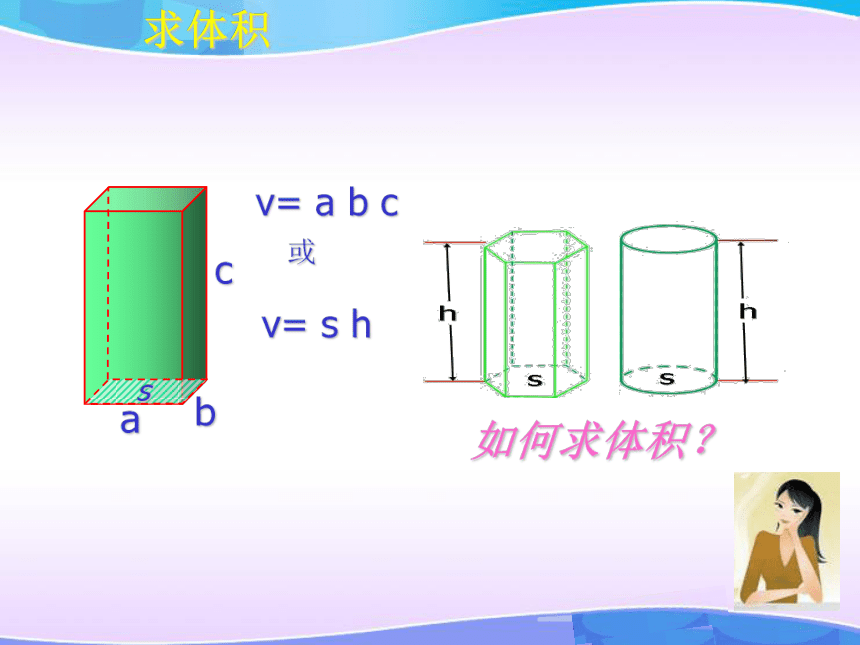
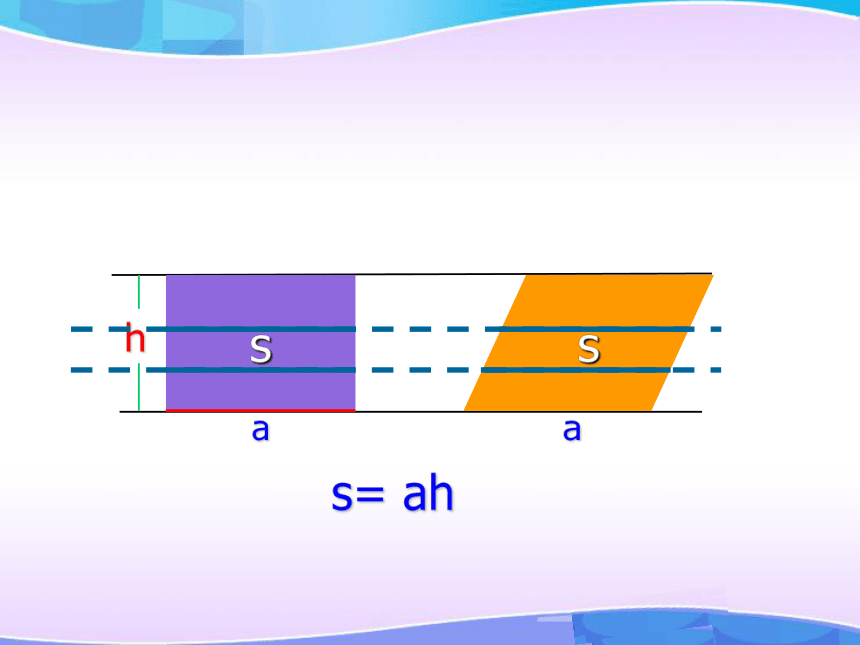
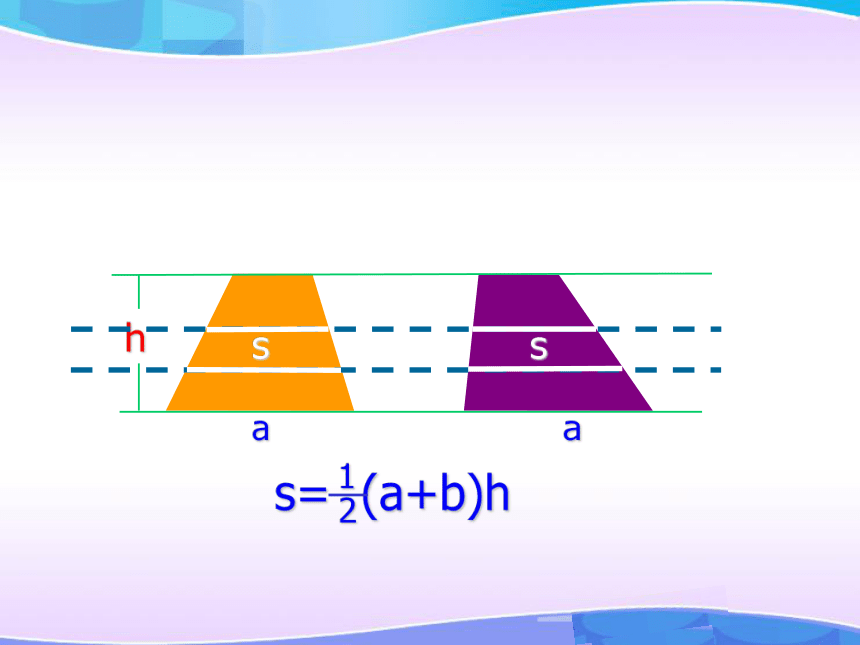
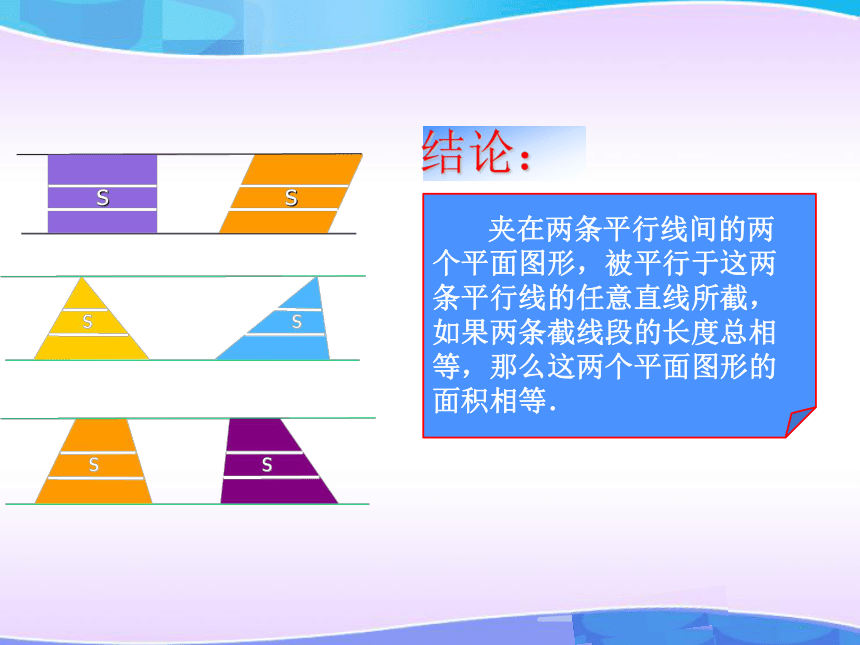
——高斯空间几何体的体积(一)提出问题如何求算体积??引入新课求水立方的体积引入新课177 m177 m31 m求水立方的体积31 m引入新课177 m177 m求水立方的体积求路基碎石的体积青藏铁路是中国奇迹的象征 假设在青藏铁路的某段路基需要碎石铺垫,已知路基的形状尺寸如图所示(单位:米),问每修建1千米铁路需要碎石多少立方米?1000124引入新课v= a b ccabv= s h或求体积s如何求体积?s= ahasshaahaahasss= (a+b)h1 夹在两条平行线间的两个平面图形,被平行于这两条平行线的任意直线所截,如果两条截线段的长度总相等,那么这两个平面图形的面积相等.结论:类比猜想 空间几何体体积相等的条件是什么?类比猜想 夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果两个截面的面积总相等,那么这两个几何体的体积相等.体积相等物理实验体积相等物理实验体积相等hVhVss底面积相等,高也相等的柱体的体积也相等。柱体的体积hVhVss体积相等几何体的体积 夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果两个截面的面积总相等,那么这两个几何体的体积相等.祖暅原理:几何体的体积数学家资料祖冲之祖暅网上学习 夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果两个截面的面积总相等,那么这两个几何体的体积相等.祖暅原理:幂势既同,则积不容异几何体的体积祖暅原理:幂势既同,则积不容异截面积几何体的高几何体的体积棱柱和圆柱的体积棱柱和圆柱的体积棱柱和圆柱的体积棱柱和圆柱的体积棱柱和圆柱的体积棱柱和圆柱的体积V柱体=Sh由祖暅原理得:ShSS1、已知正六棱柱底面边长为4cm,高为6cm,则这个正六棱柱的体积是多少?巩固应用2、圆柱体积计算青藏铁路是中国奇迹的象征 3、假设在青藏铁路的某段路基需要碎石铺垫,已知路基的形状尺寸如图所示(单位:米),问每修建1千米铁路需要碎石多少立方米?巩固应用探究问题数量:( ? )个讨论图片探究问题4、已知一个六角螺帽的底面积是正六边形, 边长为12mm, 内孔直径为10mm, 高为10mm. 求该六角螺帽的体积.其他方法?探究问题探究问题4、已知一个六角螺帽的底面积是正六边形, 边长为12mm, 内孔直径为10mm, 高为10mm. 求该六角螺帽的体积.例4:有一堆相同规格的六角螺帽毛坯共重5.8kg,已知底面六边形边长是12mm,高是10mm,内孔直径是10mm,那么约有毛坯多少个?(铁的比重是7.8g/cm3)5.8000÷(7.8×2.96)≈252(个)=2.96(cm3)答:约有毛坯252个。探究问题5、已知一个铜质的五棱柱的底面积为16cm2, 高为4cm, 现将它熔化后铸成一个正方体的铜块, 那么铸成的铜块的棱长为多少(不计损耗)?
答案:铜块的棱长为4cm探究问题今天我们学习了什么?1、祖暅原理2、棱柱体积公式今天我们学习了什么?1、在探究祖暅原理的过程中,体会了从“平面”到“空间”的类比、猜想的数学思想方法。
2、体会到了祖暅原理中由“面积都相等”推出“体积都相等”的辩证思想。
3、在推导棱柱体积公式的过程中,从特殊到一般,从一般到特殊的归纳演绎的数学思想方法很有意思。今天我们学习了什么? 我国古代数学家对几何体体积研究的成果是对人类文明的伟大贡献,激发了我们的民族自豪感。布置作业习题六 1, 2, 10(1)任意棱柱割补成长方体。
(2)课下了解数学史上求几何体
体积的发展过程。研究性学习
——拉普拉斯数学中的一些美丽定理具有这样的特性:它们极易从事实中归纳出来,但证明却隐藏得极深。
——高斯空间几何体的体积(一)提出问题如何求算体积??引入新课求水立方的体积引入新课177 m177 m31 m求水立方的体积31 m引入新课177 m177 m求水立方的体积求路基碎石的体积青藏铁路是中国奇迹的象征 假设在青藏铁路的某段路基需要碎石铺垫,已知路基的形状尺寸如图所示(单位:米),问每修建1千米铁路需要碎石多少立方米?1000124引入新课v= a b ccabv= s h或求体积s如何求体积?s= ahasshaahaahasss= (a+b)h1 夹在两条平行线间的两个平面图形,被平行于这两条平行线的任意直线所截,如果两条截线段的长度总相等,那么这两个平面图形的面积相等.结论:类比猜想 空间几何体体积相等的条件是什么?类比猜想 夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果两个截面的面积总相等,那么这两个几何体的体积相等.体积相等物理实验体积相等物理实验体积相等hVhVss底面积相等,高也相等的柱体的体积也相等。柱体的体积hVhVss体积相等几何体的体积 夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果两个截面的面积总相等,那么这两个几何体的体积相等.祖暅原理:几何体的体积数学家资料祖冲之祖暅网上学习 夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果两个截面的面积总相等,那么这两个几何体的体积相等.祖暅原理:幂势既同,则积不容异几何体的体积祖暅原理:幂势既同,则积不容异截面积几何体的高几何体的体积棱柱和圆柱的体积棱柱和圆柱的体积棱柱和圆柱的体积棱柱和圆柱的体积棱柱和圆柱的体积棱柱和圆柱的体积V柱体=Sh由祖暅原理得:ShSS1、已知正六棱柱底面边长为4cm,高为6cm,则这个正六棱柱的体积是多少?巩固应用2、圆柱体积计算青藏铁路是中国奇迹的象征 3、假设在青藏铁路的某段路基需要碎石铺垫,已知路基的形状尺寸如图所示(单位:米),问每修建1千米铁路需要碎石多少立方米?巩固应用探究问题数量:( ? )个讨论图片探究问题4、已知一个六角螺帽的底面积是正六边形, 边长为12mm, 内孔直径为10mm, 高为10mm. 求该六角螺帽的体积.其他方法?探究问题探究问题4、已知一个六角螺帽的底面积是正六边形, 边长为12mm, 内孔直径为10mm, 高为10mm. 求该六角螺帽的体积.例4:有一堆相同规格的六角螺帽毛坯共重5.8kg,已知底面六边形边长是12mm,高是10mm,内孔直径是10mm,那么约有毛坯多少个?(铁的比重是7.8g/cm3)5.8000÷(7.8×2.96)≈252(个)=2.96(cm3)答:约有毛坯252个。探究问题5、已知一个铜质的五棱柱的底面积为16cm2, 高为4cm, 现将它熔化后铸成一个正方体的铜块, 那么铸成的铜块的棱长为多少(不计损耗)?
答案:铜块的棱长为4cm探究问题今天我们学习了什么?1、祖暅原理2、棱柱体积公式今天我们学习了什么?1、在探究祖暅原理的过程中,体会了从“平面”到“空间”的类比、猜想的数学思想方法。
2、体会到了祖暅原理中由“面积都相等”推出“体积都相等”的辩证思想。
3、在推导棱柱体积公式的过程中,从特殊到一般,从一般到特殊的归纳演绎的数学思想方法很有意思。今天我们学习了什么? 我国古代数学家对几何体体积研究的成果是对人类文明的伟大贡献,激发了我们的民族自豪感。布置作业习题六 1, 2, 10(1)任意棱柱割补成长方体。
(2)课下了解数学史上求几何体
体积的发展过程。研究性学习
