15.1.1 数据有用吗 同步练习(含答案)
文档属性
| 名称 | 15.1.1 数据有用吗 同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 406.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 19:16:53 | ||
图片预览



文档简介
15.1.1 数据有用吗
一、基础练习
1.某校开展为地震灾区捐款活动,九年级(2)班第1组8名学生捐款如下(单位:元):100,50,20,20,30,10,20,15,则这组数据的众数是 ,中位数是 .
2.某次考试,5名学生的平均分是82,除学生甲外,其余4名学生的平均分是80,那学生甲的得分是( )
A.84 B.86 C.88 D.90
3.若一组数据-1,0,2,4,x的极差为7,则x的值是( )
A.-3 B.6 C.7 D.6或-3
4.数据-2,-1,0,1,2的方差是( )
A.0 B. C.2 D.4
5.在共有15人参加的“我爱祖国”演讲比赛中,参赛选手要想知道自己是否能进入前8名,只要了解自己的成绩及全部成绩的( )
A.中位数 B.众数 C.平均数 D.方差
6.射击训练中,甲、乙、丙、丁四人每人射击10次,平均环数均为8.7环,方差分别为,,,,则四人中成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
7.一次数学测试后,随机抽取5名学生的成绩如下:78,85,91,98,98.关于这组数据的说法错误的是( )
A.极差是20 B.众数是98 C.中位数是91 D.平均数是91
8.某中学随机调查了15名学生,了解他们一周在学校参加体育锻炼时间,列表如下:
锻炼时间/小时 5 6 7 8
人数 2 6 5 2
则这15名同学一周在校参加体育锻炼时间的中位数是 ,众数是 .
9.某公司招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核,甲、乙、丙各项得分如下表:
笔试 面试 体能
甲 83 79 90
乙 85 80 75
丙 80 90 73
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试、面试、体能得分分别不得低于80分,80分,70分,并按60%, 30%,10%的比例计入总分.根据规定,请你说明谁将被录用.
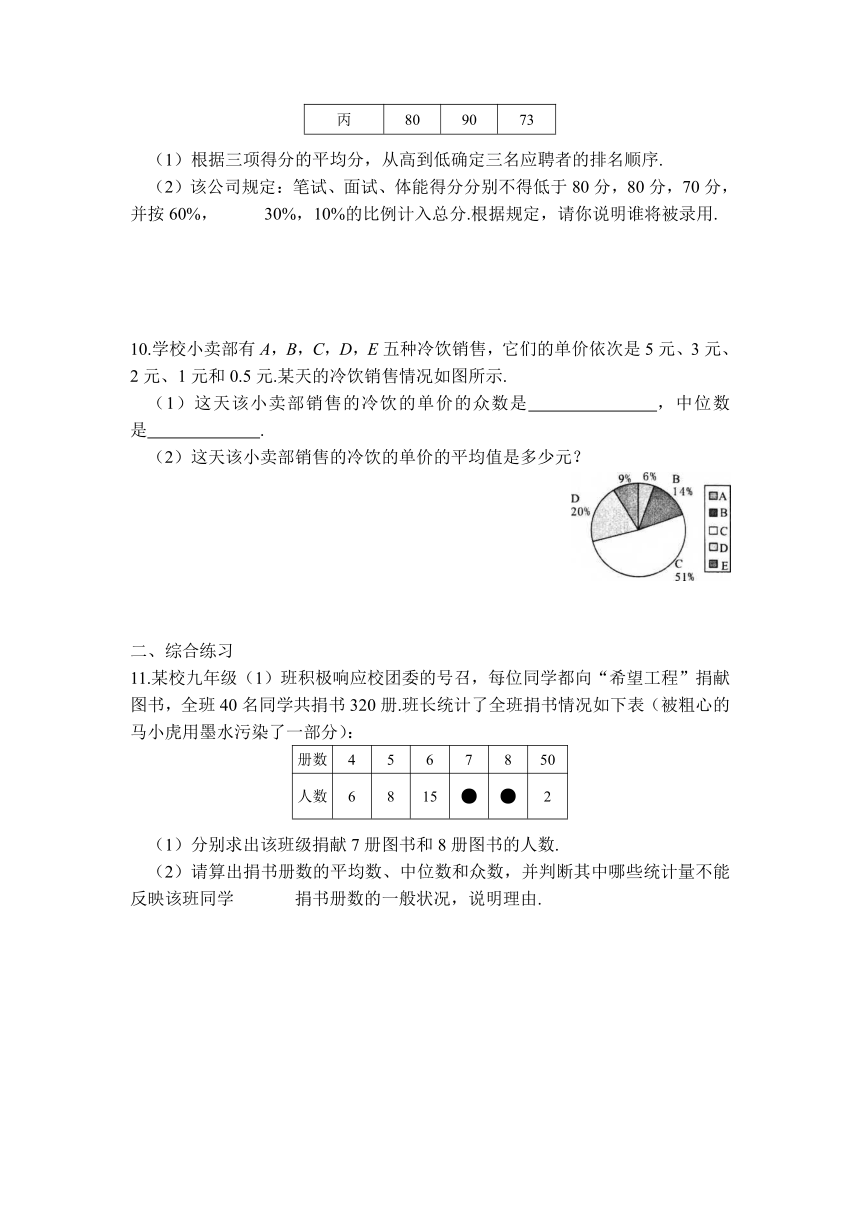
10.学校小卖部有A,B,C,D,E五种冷饮销售,它们的单价依次是5元、3元、2元、1元和0.5元.某天的冷饮销售情况如图所示.
(1)这天该小卖部销售的冷饮的单价的众数是 ,中位数是 .
(2)这天该小卖部销售的冷饮的单价的平均值是多少元?
二、综合练习
11.某校九年级(1)班积极响应校团委的号召,每位同学都向“希望工程”捐献图书,全班40名同学共捐书320册.班长统计了全班捐书情况如下表(被粗心的马小虎用墨水污染了一部分):
册数 4 5 6 7 8 50
人数 6 8 15 ● ● 2
(1)分别求出该班级捐献7册图书和8册图书的人数.
(2)请算出捐书册数的平均数、中位数和众数,并判断其中哪些统计量不能反映该班同学 捐书册数的一般状况,说明理由.
12.七年级(1)班和(2)班各推选10名同学进行投篮比赛,按照比赛规则,每人各投10个球,两个班选手的进球数统计如下表,回答下列问题.
进球数人数班级 10 9 8 7 6 5
七(1班) 1 1 1 4 0 3
七(2)班 0 1 2 5 0 2
(1)分别求七(1)班和七(2)班选手进球数的平均数、众数、中位数.
(2)如果要从这两个班中选出一个班代表年级参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?
13.王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%,现已挂果,经济效益初步显现.为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)根据样本数据请计算说明哪个山上的杨梅产量较稳定.
14.某实验中学八年级甲、乙两班分别选5名同学参加演讲比赛,其预赛成绩如下图所示:
(1)根据上图填写下表:
班级 平均数 中位数 众数 方差
甲班 8.5 8.5
乙班 8.5 10 1.6
(2)根据上表数据你认为哪班的成绩较好?并说明你的理由;
(3)乙班小明说:“我的成绩是中等水平”,你知道他是几号选手?为什么?
课后过关检测
1.数据5,2,3,2,3.
(1)这组数据的众数是 ;
(2)这组数据的中位数是 ;
(3)方差是 .
2.已知数据: 2, 5, x,8,10的平均数为6,那么x等于 .
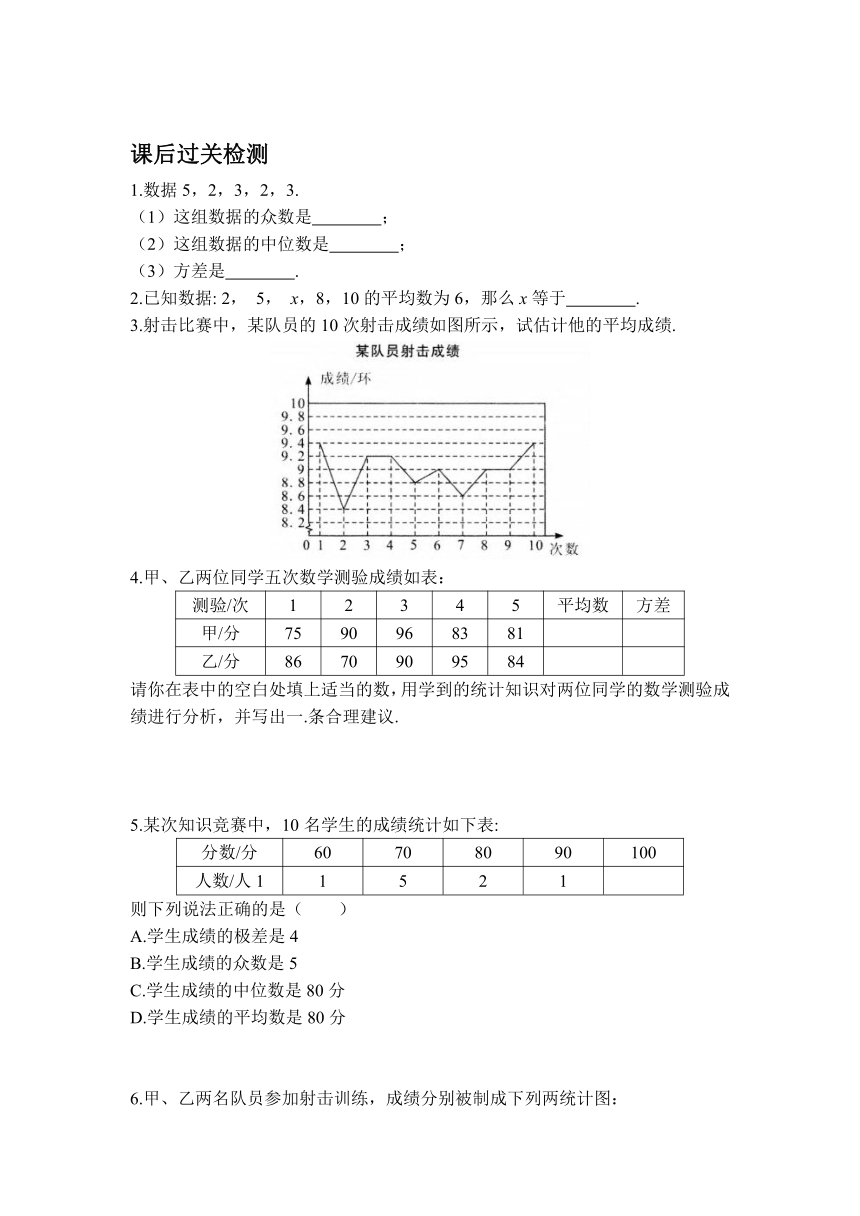
3.射击比赛中,某队员的10次射击成绩如图所示,试估计他的平均成绩.
4.甲、乙两位同学五次数学测验成绩如表:
测验/次 1 2 3 4 5 平均数 方差
甲/分 75 90 96 83 81
乙/分 86 70 90 95 84
请你在表中的空白处填上适当的数,用学到的统计知识对两位同学的数学测验成绩进行分析,并写出一.条合理建议.
5.某次知识竞赛中,10名学生的成绩统计如下表:
分数/分 60 70 80 90 100
人数/人1 1 5 2 1
则下列说法正确的是( )
A.学生成绩的极差是4
B.学生成绩的众数是5
C.学生成绩的中位数是80分
D.学生成绩的平均数是80分
6.甲、乙两名队员参加射击训练,成绩分别被制成下列两统计图:
根据以上信息,整理分析数据如下:
平均数 中位数 众数 方差
甲 a 7 7 1.2
乙 7 b 8 c
(1)写出表格中a, b, c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩,若选派其中一名参赛,你认为应选哪名队员
第6课 数据的分析习题课
1.20元 20元 2.D 3.D 4.C 5.A
6.B 7.D 8.6小时 6小时
9.解:(1)
(分)
(分)
从高到低确定的三名应聘者的排名顺序为甲、丙、乙
(2)根据题意甲被淘汰,乙:85×60%+80×30%+75×10%=82.5(分)
丙:80×60%+90×30%+73×10%=82.3(分)
∴乙将被录取。
10.(1)2元 2元
(2)平均数是:5×6%+3×14%+2×51%+1×20%+0.5×9%=1.985(元)
答:该冷饮单价平均值为1.985元。
11.解:(1)设捐献7册的人数为x,捐献8册的人数为y,
则
解得
答:捐献7册的人数为6人,捐献8册的人数为3人。
(2)平均数:320÷40=8,中位数:6 众数:6
因为平均数8受两个50的影响较大,所以平均数不能反映该班同学捐书册数的一般情况。
12.解:(1)(个)
(个)
(1)众数7个,中位数7个;
(2)众数7个,中位数7个。
(2)
(2)班选手水平发挥更稳定,争取夺得总进球数的团体第一名,应该选(2)班。
(1)班前三名选手成绩突出,分别进10个、9个、8个,如果要争取个人进球进入学校前三名,应该选择(1)班。
13.解:(1)(kg)
产量总和:100×98%×2×40=7840(kg)
(2)
∵
∴乙山上的杨梅产量较稳定。
14.解:(1)第一行填:8.5 0.7 第二行填:8
(2)从平均数看,成绩一样好,因为平均数相同
从中位数看,甲班成绩好,因为甲班中位数高
从众数看,乙班成绩好,因为乙班分数高
从方差看,甲班成绩更稳定,因为甲班的方差小
(3)5号选手,因为乙班成绩中位数是8,所以小明的成绩是8分,则小明是5号选手
课后过关检测
1.(1)2和3 (2)3 (3)1.2 2.5
3.解:9环所在横线上有3个点,另7个点中有4个在横线上部,3个在下部,因此估计他的平均成绩为9环.
计算验证他的平均成绩为:
4.
测验/次 1 2 3 4 5 平均数 方差
甲/分 75 90 96 83 81 85 53.2
乙/分 86 70 90 95 84 85 70.4
解:甲和乙的平均分相同,但甲的成绩相对而言更稳定.
建议:乙同学在学习上加强训练
5.C
6.解:(1)甲的平均成绩
a=x(5+6x2+7x4+8x2+9)=7(环)
∵乙射击的成绩从小到大重新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数b==7.5(环),
乙的方差c=x[(3-7)2+(6-7)2+(4-7)2+3x(8-7)2+2x(7-7)2+(10-7)2+(9-7)2]
=x(16+1+9+3+0+9+4)=4.2
(2)应选甲.因为甲、乙的平均分相同,但甲的方差较小,成绩较稳定.
一、基础练习
1.某校开展为地震灾区捐款活动,九年级(2)班第1组8名学生捐款如下(单位:元):100,50,20,20,30,10,20,15,则这组数据的众数是 ,中位数是 .
2.某次考试,5名学生的平均分是82,除学生甲外,其余4名学生的平均分是80,那学生甲的得分是( )
A.84 B.86 C.88 D.90
3.若一组数据-1,0,2,4,x的极差为7,则x的值是( )
A.-3 B.6 C.7 D.6或-3
4.数据-2,-1,0,1,2的方差是( )
A.0 B. C.2 D.4
5.在共有15人参加的“我爱祖国”演讲比赛中,参赛选手要想知道自己是否能进入前8名,只要了解自己的成绩及全部成绩的( )
A.中位数 B.众数 C.平均数 D.方差
6.射击训练中,甲、乙、丙、丁四人每人射击10次,平均环数均为8.7环,方差分别为,,,,则四人中成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
7.一次数学测试后,随机抽取5名学生的成绩如下:78,85,91,98,98.关于这组数据的说法错误的是( )
A.极差是20 B.众数是98 C.中位数是91 D.平均数是91
8.某中学随机调查了15名学生,了解他们一周在学校参加体育锻炼时间,列表如下:
锻炼时间/小时 5 6 7 8
人数 2 6 5 2
则这15名同学一周在校参加体育锻炼时间的中位数是 ,众数是 .
9.某公司招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核,甲、乙、丙各项得分如下表:
笔试 面试 体能
甲 83 79 90
乙 85 80 75
丙 80 90 73
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试、面试、体能得分分别不得低于80分,80分,70分,并按60%, 30%,10%的比例计入总分.根据规定,请你说明谁将被录用.
10.学校小卖部有A,B,C,D,E五种冷饮销售,它们的单价依次是5元、3元、2元、1元和0.5元.某天的冷饮销售情况如图所示.
(1)这天该小卖部销售的冷饮的单价的众数是 ,中位数是 .
(2)这天该小卖部销售的冷饮的单价的平均值是多少元?
二、综合练习
11.某校九年级(1)班积极响应校团委的号召,每位同学都向“希望工程”捐献图书,全班40名同学共捐书320册.班长统计了全班捐书情况如下表(被粗心的马小虎用墨水污染了一部分):
册数 4 5 6 7 8 50
人数 6 8 15 ● ● 2
(1)分别求出该班级捐献7册图书和8册图书的人数.
(2)请算出捐书册数的平均数、中位数和众数,并判断其中哪些统计量不能反映该班同学 捐书册数的一般状况,说明理由.
12.七年级(1)班和(2)班各推选10名同学进行投篮比赛,按照比赛规则,每人各投10个球,两个班选手的进球数统计如下表,回答下列问题.
进球数人数班级 10 9 8 7 6 5
七(1班) 1 1 1 4 0 3
七(2)班 0 1 2 5 0 2
(1)分别求七(1)班和七(2)班选手进球数的平均数、众数、中位数.
(2)如果要从这两个班中选出一个班代表年级参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?
13.王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%,现已挂果,经济效益初步显现.为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)根据样本数据请计算说明哪个山上的杨梅产量较稳定.
14.某实验中学八年级甲、乙两班分别选5名同学参加演讲比赛,其预赛成绩如下图所示:
(1)根据上图填写下表:
班级 平均数 中位数 众数 方差
甲班 8.5 8.5
乙班 8.5 10 1.6
(2)根据上表数据你认为哪班的成绩较好?并说明你的理由;
(3)乙班小明说:“我的成绩是中等水平”,你知道他是几号选手?为什么?
课后过关检测
1.数据5,2,3,2,3.
(1)这组数据的众数是 ;
(2)这组数据的中位数是 ;
(3)方差是 .
2.已知数据: 2, 5, x,8,10的平均数为6,那么x等于 .
3.射击比赛中,某队员的10次射击成绩如图所示,试估计他的平均成绩.
4.甲、乙两位同学五次数学测验成绩如表:
测验/次 1 2 3 4 5 平均数 方差
甲/分 75 90 96 83 81
乙/分 86 70 90 95 84
请你在表中的空白处填上适当的数,用学到的统计知识对两位同学的数学测验成绩进行分析,并写出一.条合理建议.
5.某次知识竞赛中,10名学生的成绩统计如下表:
分数/分 60 70 80 90 100
人数/人1 1 5 2 1
则下列说法正确的是( )
A.学生成绩的极差是4
B.学生成绩的众数是5
C.学生成绩的中位数是80分
D.学生成绩的平均数是80分
6.甲、乙两名队员参加射击训练,成绩分别被制成下列两统计图:
根据以上信息,整理分析数据如下:
平均数 中位数 众数 方差
甲 a 7 7 1.2
乙 7 b 8 c
(1)写出表格中a, b, c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩,若选派其中一名参赛,你认为应选哪名队员
第6课 数据的分析习题课
1.20元 20元 2.D 3.D 4.C 5.A
6.B 7.D 8.6小时 6小时
9.解:(1)
(分)
(分)
从高到低确定的三名应聘者的排名顺序为甲、丙、乙
(2)根据题意甲被淘汰,乙:85×60%+80×30%+75×10%=82.5(分)
丙:80×60%+90×30%+73×10%=82.3(分)
∴乙将被录取。
10.(1)2元 2元
(2)平均数是:5×6%+3×14%+2×51%+1×20%+0.5×9%=1.985(元)
答:该冷饮单价平均值为1.985元。
11.解:(1)设捐献7册的人数为x,捐献8册的人数为y,
则
解得
答:捐献7册的人数为6人,捐献8册的人数为3人。
(2)平均数:320÷40=8,中位数:6 众数:6
因为平均数8受两个50的影响较大,所以平均数不能反映该班同学捐书册数的一般情况。
12.解:(1)(个)
(个)
(1)众数7个,中位数7个;
(2)众数7个,中位数7个。
(2)
(2)班选手水平发挥更稳定,争取夺得总进球数的团体第一名,应该选(2)班。
(1)班前三名选手成绩突出,分别进10个、9个、8个,如果要争取个人进球进入学校前三名,应该选择(1)班。
13.解:(1)(kg)
产量总和:100×98%×2×40=7840(kg)
(2)
∵
∴乙山上的杨梅产量较稳定。
14.解:(1)第一行填:8.5 0.7 第二行填:8
(2)从平均数看,成绩一样好,因为平均数相同
从中位数看,甲班成绩好,因为甲班中位数高
从众数看,乙班成绩好,因为乙班分数高
从方差看,甲班成绩更稳定,因为甲班的方差小
(3)5号选手,因为乙班成绩中位数是8,所以小明的成绩是8分,则小明是5号选手
课后过关检测
1.(1)2和3 (2)3 (3)1.2 2.5
3.解:9环所在横线上有3个点,另7个点中有4个在横线上部,3个在下部,因此估计他的平均成绩为9环.
计算验证他的平均成绩为:
4.
测验/次 1 2 3 4 5 平均数 方差
甲/分 75 90 96 83 81 85 53.2
乙/分 86 70 90 95 84 85 70.4
解:甲和乙的平均分相同,但甲的成绩相对而言更稳定.
建议:乙同学在学习上加强训练
5.C
6.解:(1)甲的平均成绩
a=x(5+6x2+7x4+8x2+9)=7(环)
∵乙射击的成绩从小到大重新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数b==7.5(环),
乙的方差c=x[(3-7)2+(6-7)2+(4-7)2+3x(8-7)2+2x(7-7)2+(10-7)2+(9-7)2]
=x(16+1+9+3+0+9+4)=4.2
(2)应选甲.因为甲、乙的平均分相同,但甲的方差较小,成绩较稳定.
