1.4 分式的加法和减法 课件(共41张PPT)
文档属性
| 名称 | 1.4 分式的加法和减法 课件(共41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 19:32:57 | ||
图片预览










文档简介
(共41张PPT)
分式的加法和减法
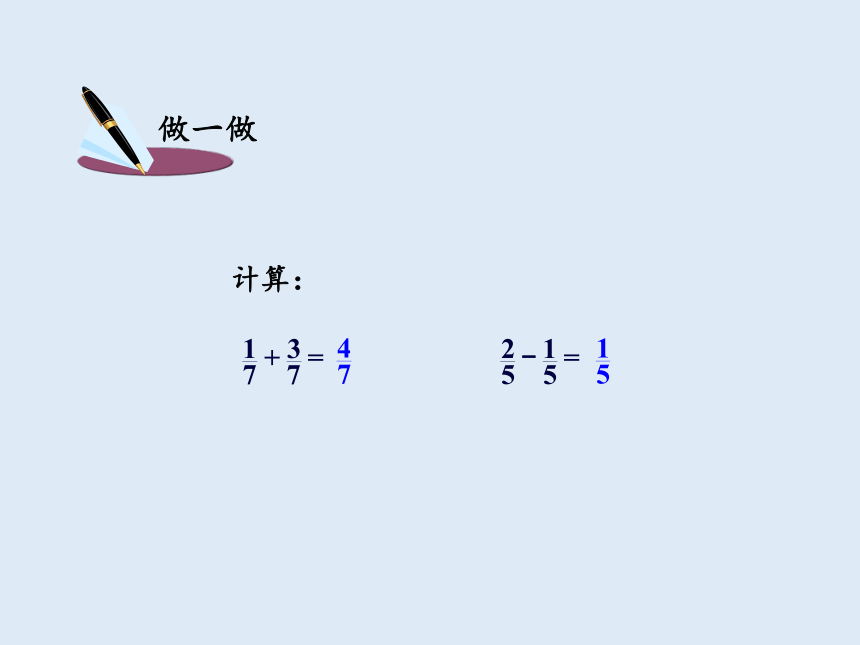
做一做
计算:
类似地,同分母的分式的加、减法运算法则是:
同分母的分式相加减,分母不变,把分子相加减
即
同分母的分数相加减,分母不变,把分子相加减。
例1 计算:
举
例
分式运算的最后结果要化为最简分式。
分式运算的最后结果要化为最简分式
注意
下列等式是否成立?为什么?
说一说
因为
所以
因为
所以
例2 计算
举
例
练习
1. 计算:
答案:x-y
2. 计算:
答案:1
中考 试题
1.化简: 的结果是( )
A.-x-y B. y-x C. x-y D. x+y
解析
A
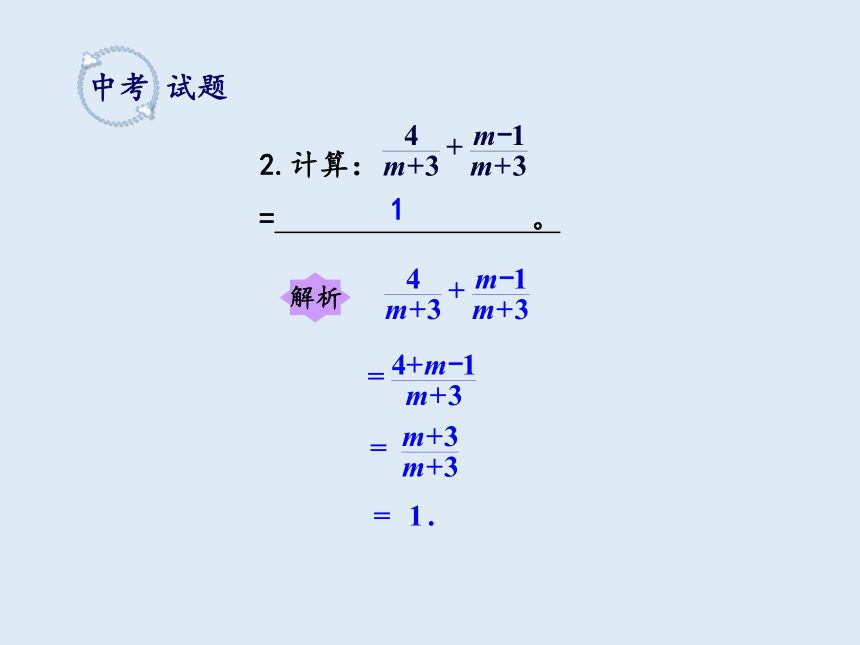
中考 试题
2.计算: = 。
解析
1
中考 试题
解析
1.当 时,原式
= 。
当 时,原式
做一做
;
.
计算:
异分母的分数相加减,要先通分,化成同分母的分数,再加减。
类似地,异分母的分式进行加、减运算时,也要先化成同分母的分式,然后再加减。
根据分式的基本性质,把几个异分母的分式化成同分母的分式的过程,叫作分式的通分。
动脑筋
如何把分式 通分?
通分时,关键是确定公分母。
一般取各分母的所有因式的最高次幂的积作为公分母,这样的公分母称为最简公分母。
两式中所有因式的最高次幂的积是6xy,
2x的因式有2,x;
3y的因式有3,y,
所以这两个分式的最简公分母为6xy。从而可以根据分式的基本性质,分别把原来各分式的分子和分母都乘同一个适当的整式,使各分式的分母都化成6xy。
2
x
3
y
通分过程如下:
举
例
例3 通分:
解 最简公分母是12xy2.
最简公分母是20a2b2c2
举
例
例4 通分:
解 最简公分母是x(x-1)
最简公分母是2(x+2)(x-2)
练习
1.通分:
2.通分:
动脑筋
从甲地到乙地依次需经过1km的上坡路和2km的下坡路。已知小明骑车在上坡路上的速度为v km/h,在下坡路上的速度为3v km/h,则他骑车从甲地到乙地需多长时间?
这是异分母的分式的加法,因此我们应先把它们化成同分母的分式,然后再相加,即
小明骑车走1km上坡路和2km下坡路的时间分别为 , ,那么骑行所需的总时间为
因此,小明骑车从甲地到乙地需
举
例
例5 计算:
解
举
例
例6 计算:
解
举
例
例7 计算:
注意
把“x+1”看作“ ”,有助于寻找两个分式的公分母。
练习
1.计算:
2.计算:
3.甲、乙两城市之间的高铁全程长1500km,列车运行速度为b km/h. 经过长时间试运行后,铁路部门决定将列车运行速度再提高50km/h,则提速后列车跑完全程要少花多长时间?
答:提速后列车跑完全程要少花
作业
谢 谢
分式的加法和减法
做一做
计算:
类似地,同分母的分式的加、减法运算法则是:
同分母的分式相加减,分母不变,把分子相加减
即
同分母的分数相加减,分母不变,把分子相加减。
例1 计算:
举
例
分式运算的最后结果要化为最简分式。
分式运算的最后结果要化为最简分式
注意
下列等式是否成立?为什么?
说一说
因为
所以
因为
所以
例2 计算
举
例
练习
1. 计算:
答案:x-y
2. 计算:
答案:1
中考 试题
1.化简: 的结果是( )
A.-x-y B. y-x C. x-y D. x+y
解析
A
中考 试题
2.计算: = 。
解析
1
中考 试题
解析
1.当 时,原式
= 。
当 时,原式
做一做
;
.
计算:
异分母的分数相加减,要先通分,化成同分母的分数,再加减。
类似地,异分母的分式进行加、减运算时,也要先化成同分母的分式,然后再加减。
根据分式的基本性质,把几个异分母的分式化成同分母的分式的过程,叫作分式的通分。
动脑筋
如何把分式 通分?
通分时,关键是确定公分母。
一般取各分母的所有因式的最高次幂的积作为公分母,这样的公分母称为最简公分母。
两式中所有因式的最高次幂的积是6xy,
2x的因式有2,x;
3y的因式有3,y,
所以这两个分式的最简公分母为6xy。从而可以根据分式的基本性质,分别把原来各分式的分子和分母都乘同一个适当的整式,使各分式的分母都化成6xy。
2
x
3
y
通分过程如下:
举
例
例3 通分:
解 最简公分母是12xy2.
最简公分母是20a2b2c2
举
例
例4 通分:
解 最简公分母是x(x-1)
最简公分母是2(x+2)(x-2)
练习
1.通分:
2.通分:
动脑筋
从甲地到乙地依次需经过1km的上坡路和2km的下坡路。已知小明骑车在上坡路上的速度为v km/h,在下坡路上的速度为3v km/h,则他骑车从甲地到乙地需多长时间?
这是异分母的分式的加法,因此我们应先把它们化成同分母的分式,然后再相加,即
小明骑车走1km上坡路和2km下坡路的时间分别为 , ,那么骑行所需的总时间为
因此,小明骑车从甲地到乙地需
举
例
例5 计算:
解
举
例
例6 计算:
解
举
例
例7 计算:
注意
把“x+1”看作“ ”,有助于寻找两个分式的公分母。
练习
1.计算:
2.计算:
3.甲、乙两城市之间的高铁全程长1500km,列车运行速度为b km/h. 经过长时间试运行后,铁路部门决定将列车运行速度再提高50km/h,则提速后列车跑完全程要少花多长时间?
答:提速后列车跑完全程要少花
作业
谢 谢
同课章节目录
