2.4 线段的垂直平分线 课件(共26张PPT)
文档属性
| 名称 | 2.4 线段的垂直平分线 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 593.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 19:41:59 | ||
图片预览





文档简介
(共26张PPT)
线段的垂直平分线
观察
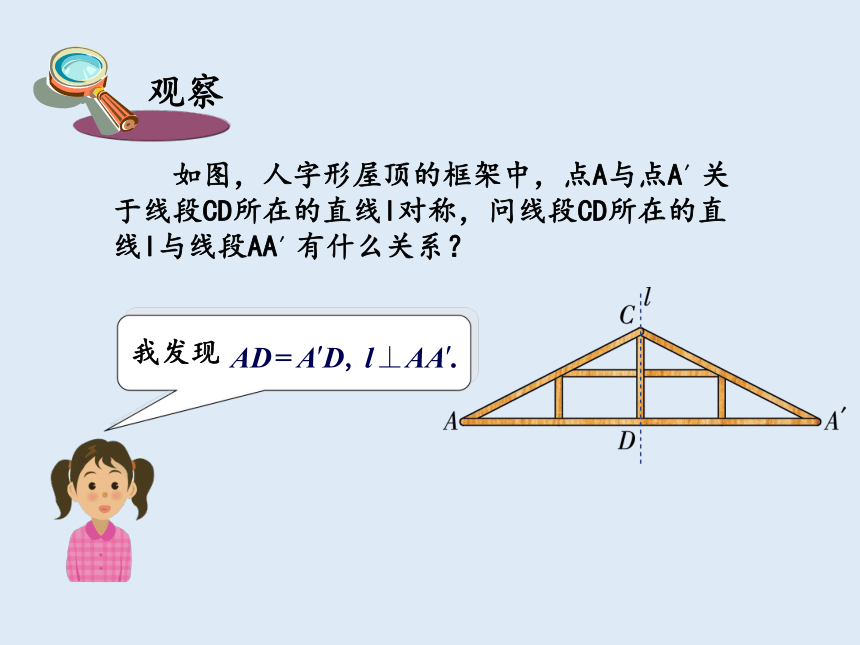
如图,人字形屋顶的框架中,点A与点A′关于线段CD所在的直线l对称,问线段CD所在的直线l与线段AA′有什么关系?
我发现
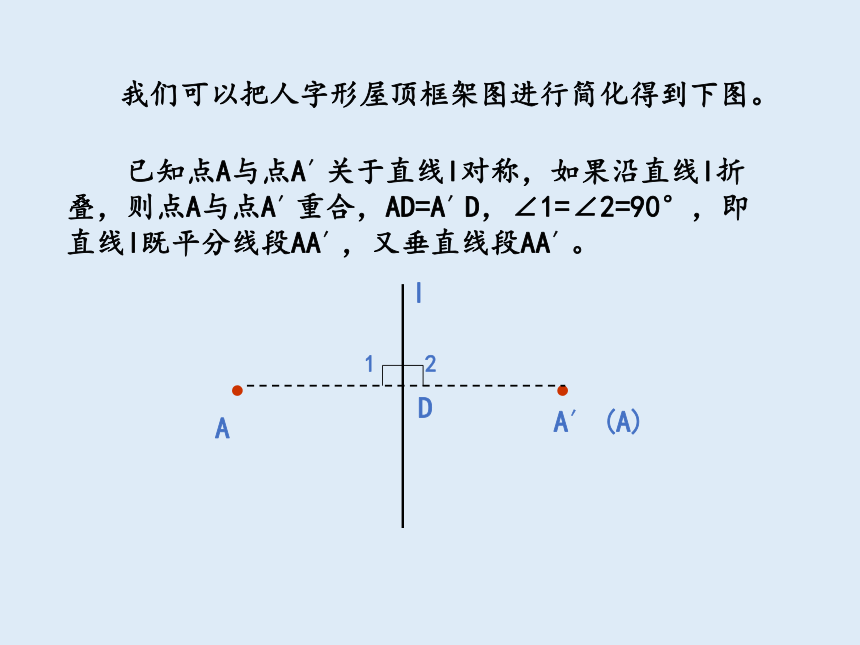
我们可以把人字形屋顶框架图进行简化得到下图。
已知点A与点A′关于直线l对称,如果沿直线l折叠,则点A与点A′重合,AD=A′D,∠1=∠2=90°,即直线l既平分线段AA′,又垂直线段AA′。
●
●
l
A
A′
D
2
1
(A)
我们把垂直且平分一条线段的直线叫作这条线段的垂直平分线。
由上可知:线段是轴对称图形,线段的垂直平分线是它的对称轴。
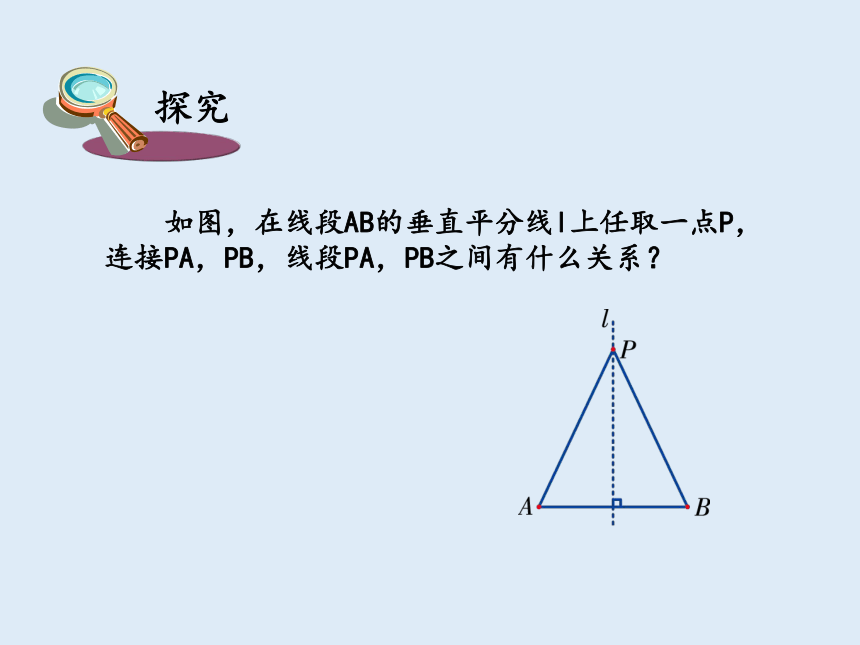
如图,在线段AB的垂直平分线l上任取一点P,连接PA,PB,线段PA,PB之间有什么关系?
探究
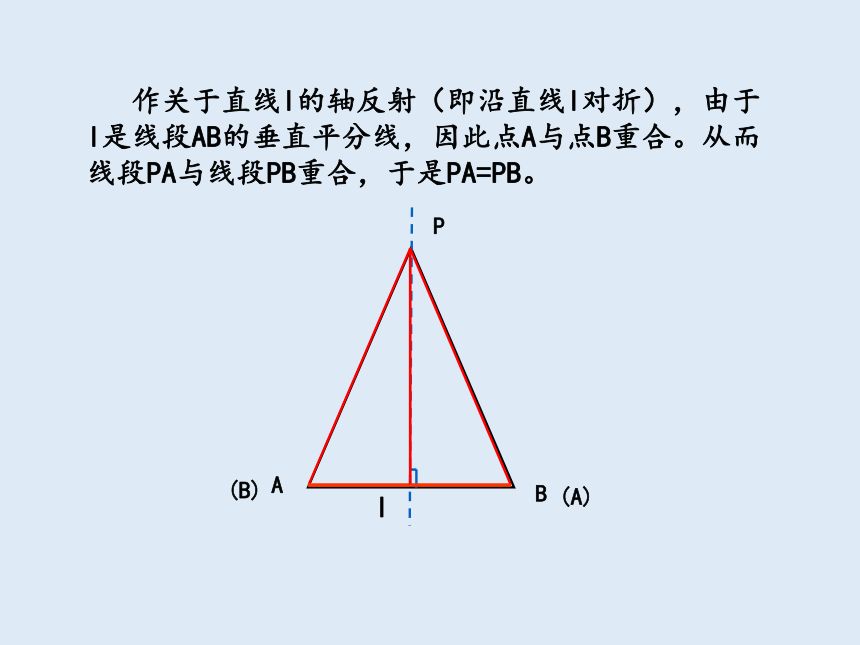
作关于直线l的轴反射(即沿直线l对折),由于l是线段AB的垂直平分线,因此点A与点B重合。从而线段PA与线段PB重合,于是PA=PB。
(A)
(B)
B
A
P
l
结论
线段垂直平分线上的点到线段两端的距离相等。
由此得出线段垂直平分线的性质定理:
动脑筋
我们知道线段垂直平分线上的点到线段两端的距离相等,反过来,如果已知一点P到线段AB两端的距离PA与PB相等,那么点P在线段AB的垂直平分线上吗?
(1)当点P在线段AB上时,
因为PA=PB,
所以点P为线段AB的中点,
显然此时点P在线段AB的垂直平分线上。
(2)当点P在线段AB外时,如下图所示。
因为PA=PB,
所以△PAB是等腰三角形。
过顶点P作PC⊥AB,垂足为点C,
从而底边AB上的高PC也是底边AB上的中线。
即PC⊥AB,且AC=BC。
因此直线PC是线段AB的垂直平分线,
此时点P也在线段AB的垂直平分线上。
结论
到线段两端距离相等的点在线段的垂直平分线上。
由此得到线段垂直平分线的性质定理的逆定理:
例 已知:如图,在△ABC中,AB,BC的垂直平分线相交于点O,连接OA,OB,OC。
求证:点O在AC的垂直平分线上。
举
例
证明 ∵点O在线段AB的垂直平分线上,
∴ OA=OB
同理OB=OC
∴ OA=OC
∴ 点O在AC的垂直平分线上。
练习
1.如图,在△ABC中,AB的垂直平分线分别交
AB,BC于点D,E,∠B=30°,∠BAC=80°, 求∠CAE的度数。
答:∠CAE=50°
2.已知:如图,点C,D是线段AB外的两点,且AC=BC,AD=BD,AB与CD相交于点O。
求证:AO=BO
证明:∵AC=BC,AD=BD,
∴
点C和点D在线段AB的垂直平分线上,
∴ CD为线段AB的垂直平分线。
又 AB与CD相交于点O
∴
AO=BO
如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于( )。
A.6cm B.8cm C.10cm D.12cm
中考 试题
解析
∵DE是AB的垂直平分线,
∴AE=BE(线段垂直平分线上的点到线段两端点的距离相等)
又∵在△BCE中,
BE+CE+BC=18cm,BC=8cm,
∴BE+CE=10cm.
∴AC=AE+CE=BE+CE=10cm.
故应选择C.
C
做一做
如图,已知线段AB,作线段AB的垂直平分线。
根据“到线段两端距离相等的点在线段的垂直平分线上”,要作线段AB的垂直平分线,关键是找出到线段AB两端距离相等的两点。
作法
①分别以点A,B为圆心,以大于 AB的长为半径画弧,两弧相交于点C和点D;
②过点C,D作直线CD,则直线CD就是线段AB的垂直平分线。
因为线段AB的垂直平分线CD与线段AB的交点就是线段AB的中点,所以可以用这种方法作出线段的中点。
动脑筋
如何过一点P作已知直线l的垂线呢?
由于两点确定一条直线,因此我们可以通过在已知直线上作线段的垂直平分线来找出垂线上的另一点,从而确定已知直线的垂线。
(1)当点P在直线l上。
(2)当点P在直线l外。
点P与已知直线l的位置关系有两种:
①在直线l上点P的两旁分别截取线段PA,PB,使PA=PB;
(1)当点P在直线l上
②分别以A,B为圆心以大于 AB的长为半径画弧,两弧相交于点C;
③过点C,P作直线CP,则直线CP为所求作的直线。
(2)当点P在直线l外
①以点P为圆心,以大于点P到直线l的距离的线段长为半径画弧,交直线l于点A,B;
②分别以A,B为圆心以大于 AB的长为半径画弧,两弧相交于点C;
③过点C,P作直线CP,则直线CP为所求作的直线。
用尺规完成下列作图(只保留作图痕迹,不要
求写出作法)。
1.如图,在直线l上求作一点P,使PA=PB。
练习
2.如图,作出△ABC的BC边上的高。
作业
谢 谢
线段的垂直平分线
观察
如图,人字形屋顶的框架中,点A与点A′关于线段CD所在的直线l对称,问线段CD所在的直线l与线段AA′有什么关系?
我发现
我们可以把人字形屋顶框架图进行简化得到下图。
已知点A与点A′关于直线l对称,如果沿直线l折叠,则点A与点A′重合,AD=A′D,∠1=∠2=90°,即直线l既平分线段AA′,又垂直线段AA′。
●
●
l
A
A′
D
2
1
(A)
我们把垂直且平分一条线段的直线叫作这条线段的垂直平分线。
由上可知:线段是轴对称图形,线段的垂直平分线是它的对称轴。
如图,在线段AB的垂直平分线l上任取一点P,连接PA,PB,线段PA,PB之间有什么关系?
探究
作关于直线l的轴反射(即沿直线l对折),由于l是线段AB的垂直平分线,因此点A与点B重合。从而线段PA与线段PB重合,于是PA=PB。
(A)
(B)
B
A
P
l
结论
线段垂直平分线上的点到线段两端的距离相等。
由此得出线段垂直平分线的性质定理:
动脑筋
我们知道线段垂直平分线上的点到线段两端的距离相等,反过来,如果已知一点P到线段AB两端的距离PA与PB相等,那么点P在线段AB的垂直平分线上吗?
(1)当点P在线段AB上时,
因为PA=PB,
所以点P为线段AB的中点,
显然此时点P在线段AB的垂直平分线上。
(2)当点P在线段AB外时,如下图所示。
因为PA=PB,
所以△PAB是等腰三角形。
过顶点P作PC⊥AB,垂足为点C,
从而底边AB上的高PC也是底边AB上的中线。
即PC⊥AB,且AC=BC。
因此直线PC是线段AB的垂直平分线,
此时点P也在线段AB的垂直平分线上。
结论
到线段两端距离相等的点在线段的垂直平分线上。
由此得到线段垂直平分线的性质定理的逆定理:
例 已知:如图,在△ABC中,AB,BC的垂直平分线相交于点O,连接OA,OB,OC。
求证:点O在AC的垂直平分线上。
举
例
证明 ∵点O在线段AB的垂直平分线上,
∴ OA=OB
同理OB=OC
∴ OA=OC
∴ 点O在AC的垂直平分线上。
练习
1.如图,在△ABC中,AB的垂直平分线分别交
AB,BC于点D,E,∠B=30°,∠BAC=80°, 求∠CAE的度数。
答:∠CAE=50°
2.已知:如图,点C,D是线段AB外的两点,且AC=BC,AD=BD,AB与CD相交于点O。
求证:AO=BO
证明:∵AC=BC,AD=BD,
∴
点C和点D在线段AB的垂直平分线上,
∴ CD为线段AB的垂直平分线。
又 AB与CD相交于点O
∴
AO=BO
如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于( )。
A.6cm B.8cm C.10cm D.12cm
中考 试题
解析
∵DE是AB的垂直平分线,
∴AE=BE(线段垂直平分线上的点到线段两端点的距离相等)
又∵在△BCE中,
BE+CE+BC=18cm,BC=8cm,
∴BE+CE=10cm.
∴AC=AE+CE=BE+CE=10cm.
故应选择C.
C
做一做
如图,已知线段AB,作线段AB的垂直平分线。
根据“到线段两端距离相等的点在线段的垂直平分线上”,要作线段AB的垂直平分线,关键是找出到线段AB两端距离相等的两点。
作法
①分别以点A,B为圆心,以大于 AB的长为半径画弧,两弧相交于点C和点D;
②过点C,D作直线CD,则直线CD就是线段AB的垂直平分线。
因为线段AB的垂直平分线CD与线段AB的交点就是线段AB的中点,所以可以用这种方法作出线段的中点。
动脑筋
如何过一点P作已知直线l的垂线呢?
由于两点确定一条直线,因此我们可以通过在已知直线上作线段的垂直平分线来找出垂线上的另一点,从而确定已知直线的垂线。
(1)当点P在直线l上。
(2)当点P在直线l外。
点P与已知直线l的位置关系有两种:
①在直线l上点P的两旁分别截取线段PA,PB,使PA=PB;
(1)当点P在直线l上
②分别以A,B为圆心以大于 AB的长为半径画弧,两弧相交于点C;
③过点C,P作直线CP,则直线CP为所求作的直线。
(2)当点P在直线l外
①以点P为圆心,以大于点P到直线l的距离的线段长为半径画弧,交直线l于点A,B;
②分别以A,B为圆心以大于 AB的长为半径画弧,两弧相交于点C;
③过点C,P作直线CP,则直线CP为所求作的直线。
用尺规完成下列作图(只保留作图痕迹,不要
求写出作法)。
1.如图,在直线l上求作一点P,使PA=PB。
练习
2.如图,作出△ABC的BC边上的高。
作业
谢 谢
同课章节目录
