14.1.4.2多项式乘以多项式 课件(26张PPT)
文档属性
| 名称 | 14.1.4.2多项式乘以多项式 课件(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-22 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
14.1.4.2多项式乘以多项式
人教版八年级上册
教学目标
1、掌握多项式的乘法法则。
2、会进行多项式的乘法运算。
3、结合教学内容渗透“转化”思想,发展学生的数学能力。
重点:多项式的乘法法则及其应用
难点:多项式乘法法则的应用。
新知导入
1.如何进行单项式与多项式乘法的运算?
(2)再把所得的积相加.
(1)将单项式分别乘以多项式的各项.
2.进行单项式与多项式乘法运算时,要注意什么
(1)不能漏乘:
即单项式要乘多项式的每一项.
(2)去括号时注意符号的变化.
新知讲解
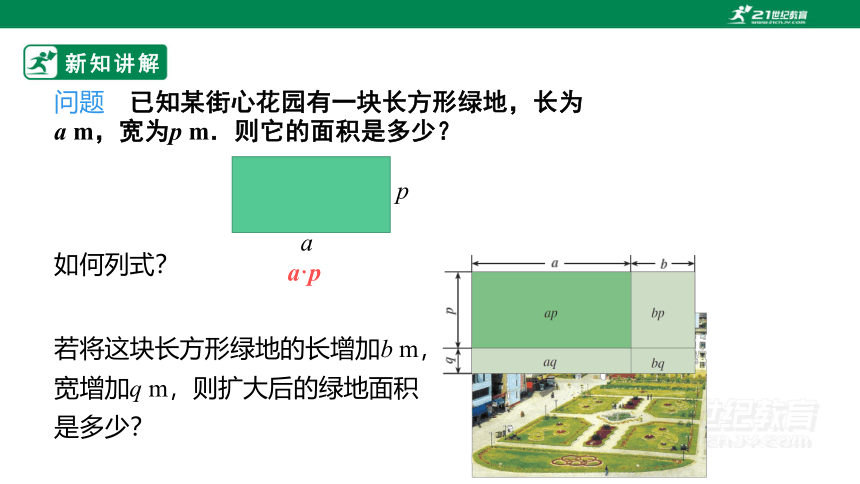
问题 已知某街心花园有一块长方形绿地,长为a m,宽为p m.则它的面积是多少?
如何列式?
a·p
a
p
若将这块长方形绿地的长增加b m,宽增加q m,则扩大后的绿地面积是多少?
新知讲解
方法一:看作一个长方形,计算它的面积.
a+b
p+q
扩大后的绿地面积为:(a+b)(p+q)
新知讲解
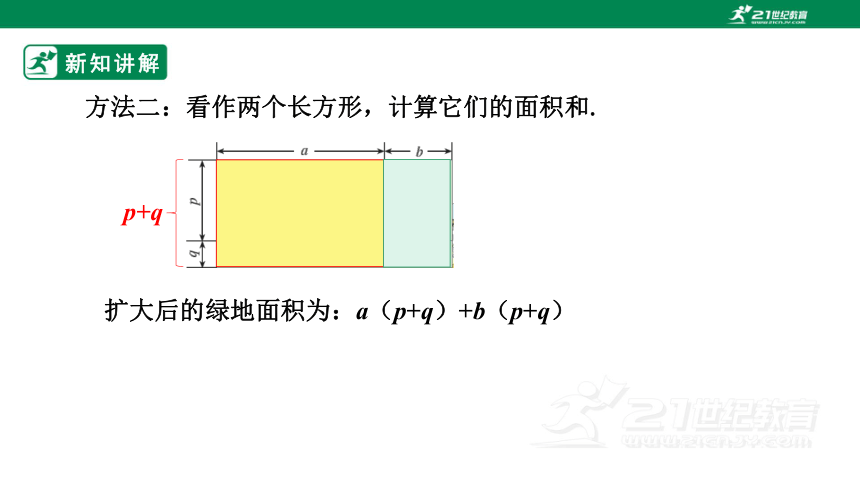
方法二:看作两个长方形,计算它们的面积和.
p+q
扩大后的绿地面积为:a(p+q)+b(p+q)
新知讲解
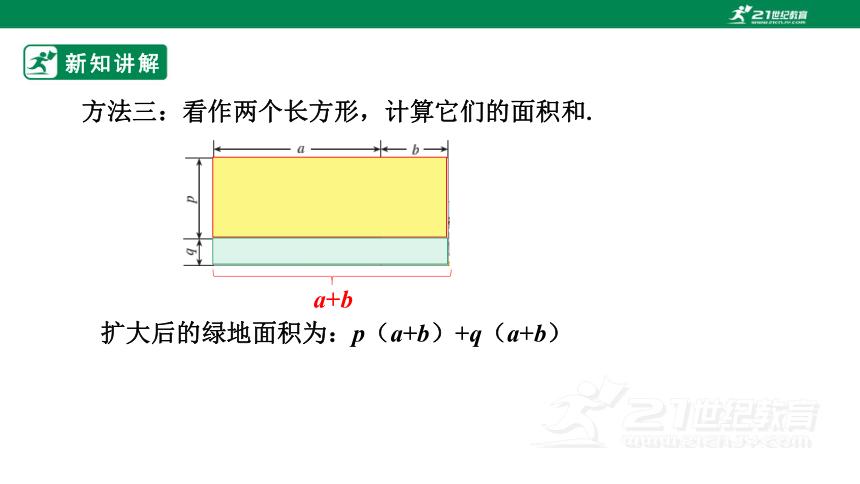
方法三:看作两个长方形,计算它们的面积和.
a+b
扩大后的绿地面积为:p(a+b)+q(a+b)
新知讲解
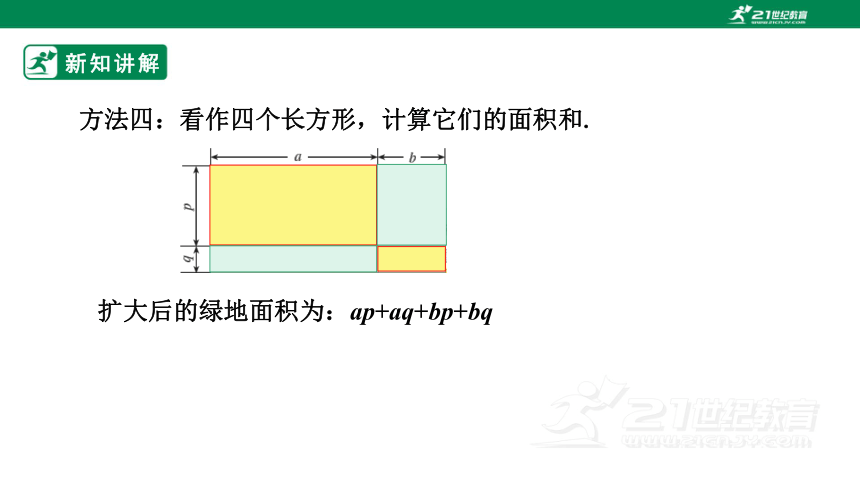
方法四:看作四个长方形,计算它们的面积和.
扩大后的绿地面积为:ap+aq+bp+bq
新知讲解
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=
ma
+ mb
+ na
+ nb
如何进行多项式与多项式相乘的运算?
实际上,把(a+b)看成一个整体,有:
= ma+mb+na+nb
(m+n)(a+b)
= m(a+b)+n(a+b)
(m+n)X=
mX+nX
?
若X=a+b,如何计算?
新知讲解
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
“多乘多” 顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
多项式乘以多项式
例题讲解
例1 计算: (1)(3x+1)(x+2); (2)(x–8y)(x–y);
解: (1) 原式=3x·x+2·3x+1·x+1×2
=3x2+6x+x+2
(2) 原式=x·x–xy–8xy+8y2
结果中有同类项的要合并同类项.
=3x2+7x+2;
计算时要注意符号问题.
=x2–9xy+8y2;
(3) 原式=x·x2–x·xy+xy2+x2y–xy2+y·y2
=x3–x2y+xy2+x2y–xy2+y3= x3+y3.
(3) (x+y)(x2–xy+y2).
计算时不能漏乘.
新知讲解
1
2
单项式必须和多项式中的每一项相乘,不能漏乘,也不要重复.
对于混合运算,要注意运算顺序,先算积的乘方与幂的乘方,再算乘法,最后结果中有同类项的要合并同类项.
在运用法则计算时,应该注意什么问题?
思考
1.计算:
(1)(2x+1)(x+3); (2)(m+2n)(3n-m);
(3)(a- 1) ; (4)(a+3b)(a-3b);
(5)(2x2-1)(x- 4) ; (6)(x2+2x+3)(2x- 5).
强化练习
【课本P102 练习 第1题】
强化练习
2.计算:
(1)( x+2 )( x+3 ); (2)( x- 4 )( x+1 );
(3)( y+4 ) ( y- 2 ); (4)( y- 5 )( y-3 ).
【课本P102 练习 第2题】
例题讲解
例2 先化简,再求值:(a–2b)(a2+2ab+4b2)–a(a–5b)(a+3b),其中a=–1,b=1.
当a=–1,b=1时,
解:原式=a3–8b3–(a2–5ab)(a+3b)
=a3–8b3–a3–3a2b+5a2b+15ab2
=–8b3+2a2b+15ab2.
原式=–8+2–15=–21.
例题讲解
由上面计算的结果找规律,观察右图,填空:
(x+p)(x+q) =( )2+ ( )x+( )
例3 确定(x+3)(x+p)=x2+mx+36中m和p的值.
解:(x+3)(x+p)=x2+xp+3x+3p
=x2+(p+3)x+3p
又∵(x+3)(x+p)=x2+mx+36
∴x2+(p+3)x+3p=x2+mx+36
∴p=12,m=p+3=15
【课本P102 练习 第2题】
强化练习
3. 确定下列各式中 m 的值:
(1)(x+4)(x+9) = x2 +mx + 36;
(2)(x-2)(x-18) = x2 + mx + 36;
【课本P106 练习 第15题】
强化练习
(3)(x+3)(x+p) = x2 +mx + 36;
【课本P106 练习 第15题】
强化练习
(4)(x-6)(x-p) = x2 + mx + 36;
【课本P106 练习 第15题】
强化练习
(5)(x+p)(x+q) = x2 + mx + 36,p,q为正整数.
【课本P106 练习 第15题】
课堂小结
多项式乘多项式
运算法则
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)=am+an+bm+bn
注意
不要漏乘;正确确定各项符号;结果要最简.
实质上是转化为单项式乘多项式的运算.
(x–1)2在一般情况下不等于x2–12.
拓展提高
1、解方程与不等式:
①(x–3)(x–2)+18=(x+9)(x+1);②(3x+6)(3x–6)<9(x–2)(x+3).
解:①原式去括号,得:x2–5x+6+18=x2+10x+9,
移项合并,得:15x=15,
解得:x=1;
②原式去括号,得:9x2–36<9x2+9x–54,
移项合并,得:9x>18,
解得:x>2 .
【课本P106 练习 第14题】
拓展提高
2、计算图中阴影所示绿地的面积(长度单位:m).
【课本P106 练习 第11题】
拓展提高
3、 已知ax2+bx+1(a≠0)与3x–2的积不含x2项,也不含x项,求系数a、b的值.
解:(ax2+bx+1)(3x–2)
=3ax3–2ax2+3bx2–2bx+3x–2,
∵积不含x2的项,也不含x的项,
方法总结:解决此类问题首先要利用多项式乘法法则计算出展开式,合并同类项后,再根据不含某一项,可得这一项系数等于零,再列出方程(组)解答.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
14.1.4.2多项式乘以多项式
人教版八年级上册
教学目标
1、掌握多项式的乘法法则。
2、会进行多项式的乘法运算。
3、结合教学内容渗透“转化”思想,发展学生的数学能力。
重点:多项式的乘法法则及其应用
难点:多项式乘法法则的应用。
新知导入
1.如何进行单项式与多项式乘法的运算?
(2)再把所得的积相加.
(1)将单项式分别乘以多项式的各项.
2.进行单项式与多项式乘法运算时,要注意什么
(1)不能漏乘:
即单项式要乘多项式的每一项.
(2)去括号时注意符号的变化.
新知讲解
问题 已知某街心花园有一块长方形绿地,长为a m,宽为p m.则它的面积是多少?
如何列式?
a·p
a
p
若将这块长方形绿地的长增加b m,宽增加q m,则扩大后的绿地面积是多少?
新知讲解
方法一:看作一个长方形,计算它的面积.
a+b
p+q
扩大后的绿地面积为:(a+b)(p+q)
新知讲解
方法二:看作两个长方形,计算它们的面积和.
p+q
扩大后的绿地面积为:a(p+q)+b(p+q)
新知讲解
方法三:看作两个长方形,计算它们的面积和.
a+b
扩大后的绿地面积为:p(a+b)+q(a+b)
新知讲解
方法四:看作四个长方形,计算它们的面积和.
扩大后的绿地面积为:ap+aq+bp+bq
新知讲解
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=
ma
+ mb
+ na
+ nb
如何进行多项式与多项式相乘的运算?
实际上,把(a+b)看成一个整体,有:
= ma+mb+na+nb
(m+n)(a+b)
= m(a+b)+n(a+b)
(m+n)X=
mX+nX
?
若X=a+b,如何计算?
新知讲解
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
“多乘多” 顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
多项式乘以多项式
例题讲解
例1 计算: (1)(3x+1)(x+2); (2)(x–8y)(x–y);
解: (1) 原式=3x·x+2·3x+1·x+1×2
=3x2+6x+x+2
(2) 原式=x·x–xy–8xy+8y2
结果中有同类项的要合并同类项.
=3x2+7x+2;
计算时要注意符号问题.
=x2–9xy+8y2;
(3) 原式=x·x2–x·xy+xy2+x2y–xy2+y·y2
=x3–x2y+xy2+x2y–xy2+y3= x3+y3.
(3) (x+y)(x2–xy+y2).
计算时不能漏乘.
新知讲解
1
2
单项式必须和多项式中的每一项相乘,不能漏乘,也不要重复.
对于混合运算,要注意运算顺序,先算积的乘方与幂的乘方,再算乘法,最后结果中有同类项的要合并同类项.
在运用法则计算时,应该注意什么问题?
思考
1.计算:
(1)(2x+1)(x+3); (2)(m+2n)(3n-m);
(3)(a- 1) ; (4)(a+3b)(a-3b);
(5)(2x2-1)(x- 4) ; (6)(x2+2x+3)(2x- 5).
强化练习
【课本P102 练习 第1题】
强化练习
2.计算:
(1)( x+2 )( x+3 ); (2)( x- 4 )( x+1 );
(3)( y+4 ) ( y- 2 ); (4)( y- 5 )( y-3 ).
【课本P102 练习 第2题】
例题讲解
例2 先化简,再求值:(a–2b)(a2+2ab+4b2)–a(a–5b)(a+3b),其中a=–1,b=1.
当a=–1,b=1时,
解:原式=a3–8b3–(a2–5ab)(a+3b)
=a3–8b3–a3–3a2b+5a2b+15ab2
=–8b3+2a2b+15ab2.
原式=–8+2–15=–21.
例题讲解
由上面计算的结果找规律,观察右图,填空:
(x+p)(x+q) =( )2+ ( )x+( )
例3 确定(x+3)(x+p)=x2+mx+36中m和p的值.
解:(x+3)(x+p)=x2+xp+3x+3p
=x2+(p+3)x+3p
又∵(x+3)(x+p)=x2+mx+36
∴x2+(p+3)x+3p=x2+mx+36
∴p=12,m=p+3=15
【课本P102 练习 第2题】
强化练习
3. 确定下列各式中 m 的值:
(1)(x+4)(x+9) = x2 +mx + 36;
(2)(x-2)(x-18) = x2 + mx + 36;
【课本P106 练习 第15题】
强化练习
(3)(x+3)(x+p) = x2 +mx + 36;
【课本P106 练习 第15题】
强化练习
(4)(x-6)(x-p) = x2 + mx + 36;
【课本P106 练习 第15题】
强化练习
(5)(x+p)(x+q) = x2 + mx + 36,p,q为正整数.
【课本P106 练习 第15题】
课堂小结
多项式乘多项式
运算法则
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)=am+an+bm+bn
注意
不要漏乘;正确确定各项符号;结果要最简.
实质上是转化为单项式乘多项式的运算.
(x–1)2在一般情况下不等于x2–12.
拓展提高
1、解方程与不等式:
①(x–3)(x–2)+18=(x+9)(x+1);②(3x+6)(3x–6)<9(x–2)(x+3).
解:①原式去括号,得:x2–5x+6+18=x2+10x+9,
移项合并,得:15x=15,
解得:x=1;
②原式去括号,得:9x2–36<9x2+9x–54,
移项合并,得:9x>18,
解得:x>2 .
【课本P106 练习 第14题】
拓展提高
2、计算图中阴影所示绿地的面积(长度单位:m).
【课本P106 练习 第11题】
拓展提高
3、 已知ax2+bx+1(a≠0)与3x–2的积不含x2项,也不含x项,求系数a、b的值.
解:(ax2+bx+1)(3x–2)
=3ax3–2ax2+3bx2–2bx+3x–2,
∵积不含x2的项,也不含x的项,
方法总结:解决此类问题首先要利用多项式乘法法则计算出展开式,合并同类项后,再根据不含某一项,可得这一项系数等于零,再列出方程(组)解答.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
