14.2.1平方差公式 课件(24张PPT)
文档属性
| 名称 | 14.2.1平方差公式 课件(24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 00:10:44 | ||
图片预览






文档简介
(共24张PPT)
14.2.1平方差公式
人教版八年级上册
教学目标
1、理解并掌握公式的结构特征,会用平方差公式运算。
2、经历探索平方差公式的过程,学会观察、发现规律并归纳、概括,
3、体验数学活动充满着创造性和探索性,并在数学活动中体验成功的喜悦
重点:平方差公式的推导和应用
难点:理解平方差公式的结构特征,灵活运用平方差公式。
复习回顾
多项式与多项式是如何相乘的?
(x + 3)( x+5)
=x2
+5x
+3x
+15
=x2
+8x
+15.
(a+b)(m+n)
=am
+an
+bm
+bn
新知讲解
①(x + 1)( x–1);
②(m + 2)( m–2);
③(2m+ 1)(2m–1);
④(5y + z)(5y–z).
计算下列多项式的积,你能发现什么规律?
做一做
x2 – 12
m2–22
(2m)2 – 12
(5y)2 – z2
这些计算结果有什么特点?
想一想
新知讲解
(a+b)(a b)=
a2 b2
两数和与这两数差的积,等于这两个数的平方差.
公式变形:
1.(a – b ) ( a + b) = a2 – b2
2.(b + a )( –b + a ) = a2 – b2
平方差公式
新知讲解
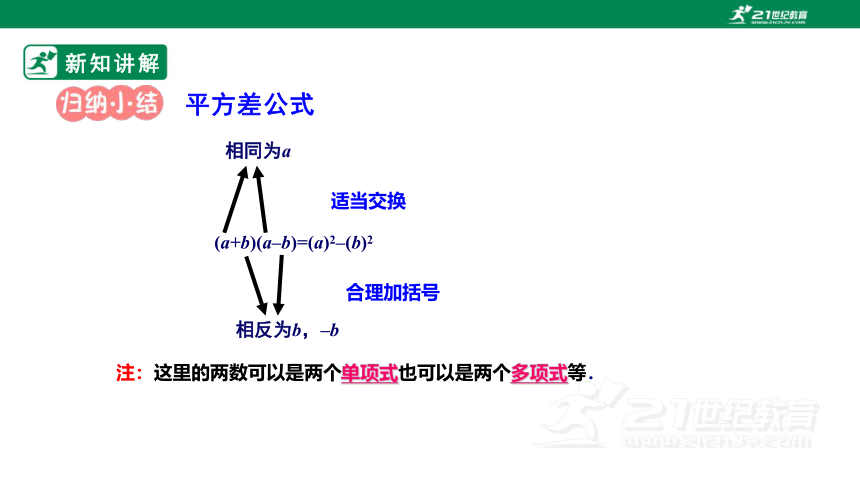
注:这里的两数可以是两个单项式也可以是两个多项式等.
(a+b)(a–b)=(a)2–(b)2
相同为a
相反为b,–b
适当交换
合理加括号
平方差公式
新知讲解
公式中的a和b,既可以是具体的数,也可以是单项
式或者多项式;
2. 左边是两个二项式的积,并且有一项完全相同,另
一项互为相反数;
3. 右边是相同项的平方减去相反项的绝对值的平方.
(a+b)(a– b)=
a2– b2.
温馨提示
新知讲解
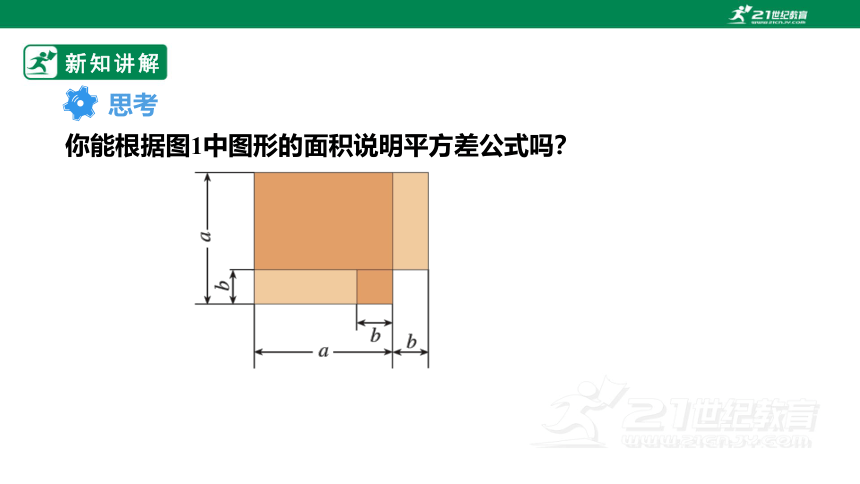
你能根据图1中图形的面积说明平方差公式吗?
思考
新知讲解
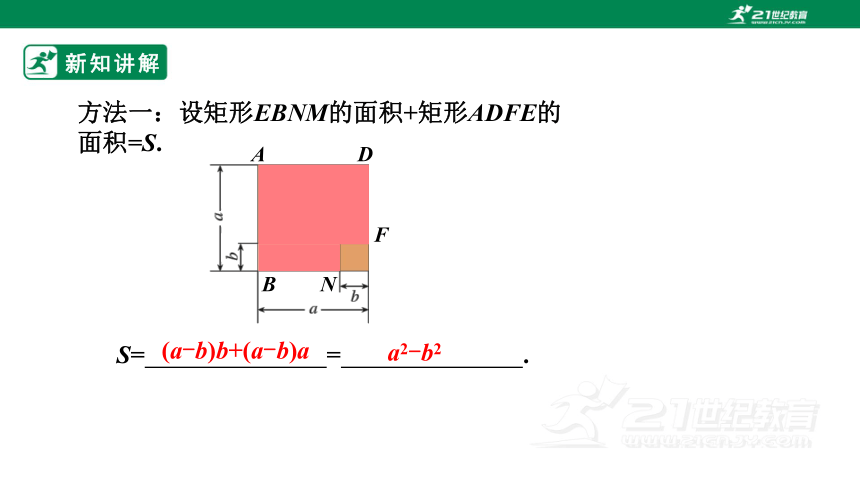
方法一:设矩形EBNM的面积+矩形ADFE的面积=S.
S= = .
A
D
F
E
B
N
M
(a-b)b+(a-b)a
a2-b2
新知讲解
方法二:剪下矩形EBNM拼到FBND的位置,如图.
S=S四边形AEBN = .
A
D(M)
N
E
B
N
M
B
(a-b)(a+b)
新知讲解
(1)(3x+2)(3x-2); (2)(-x+2y)(-x-2y).
3x
例 运用平方差公式计算:
(1)中,可以将 看作a,将 看作b,计算结果是 . (2)中,可以将 看作a,将 看作b,计算结果是 .
2
9x2 -4
-x
2y
x2 -4y2
(2) 原式= (–x)2 – (2y)2
= x2 – 4y2.
解: (1)原式=(3x)2–22
=9x2–4;
易错警示:
当相同项带有“负号”时,必须用括号括起来.
强化练习
【课本P108 练习 第1题】
1.下面各式的计算对不对?如果不对,应当怎样改正?
(1)(x+2)(x-2) =x2-2
(2)(-3a-2)(3a-2) =9a2-4
强化练习
运用平方差公式计算:
(1)( x-y)( x+y); (2)(xy+1)(xy-1);
(3)(2a-3b)(3b+2a); (4)(-2b-5)(2b-5);
【课本P112 第1题】
例题讲解
例2 计算:
(1) 102×98; (2) (y+2) (y–2) – (y–1) (y+5) .
= 1002–22
解: (1) 102×98
=10000 – 4
=(100+2)(100–2)
=9996;
= y2–4–y2–4y+5
(2)(y+2)(y–2)– (y–1)(y+5)
= y2–22–(y2+4y–5)
= – 4y + 1.
通过合理变形,利用平方差公式,可以简化运算.
不符合平方差公式运算条件的乘法,按乘法法则进行运算.
强化练习
【课本P108 练习 第2题】
3.运用平方差公式计算:
(1)(a+3b)(a-3b) (2)(3+2a)(-3+2a)
强化练习
【课本P108 练习 第2题】
3.运用平方差公式计算:
(3)51×49 (4)(3x+4)(3x-4) -(2x+3)(3x-2)
例题讲解
例3 对于任意的正整数n,整式(3n+1)(3n–1)–(3–n)(3+n)的值一定是10的整数倍吗?
即(3n+1)(3n–1)–(3–n)(3+n)的值是10的倍数.
解:原式=9n2–1–(9–n2)
=10n2–10.
∵(10n2–10)÷10=n2–1.
n为正整数,
∴n2–1为整数
强化练习
4.如果两个连续奇数分别是2n–1,2n+1(其中n为正整数),证明两个连续奇数的平方差是8的倍数.
证明:(2n+1)2–(2n–1)2
=[(2n+1)+(2n–1)][(2n+1)–(2n–1)]
=(2n+1+2n–1)(2n+1–2n+1)
=4n×2
=8n
因为8n是8的倍数,所以结论成立.
课堂小结
平方差公式
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差.
1.符号表示:(a+b)(a–b)=a2–b2
2.紧紧抓住 “一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式;对于不能直接应用公式的,可能要经过变形才可以应用.
拓展提高
1、先化简,再求值:(x+1)(x–1) +x2(1–x) +x3,其中x=2.
解:原式=x2–1+x2–x3+x3
=2x2–1.
将x=2代入上式,
原式=2×22–1=7.
拓展提高
2、解方程组
(x+2)2-(y-3)2 = (x+y)(x-y),
x-3y = 2.
【课本P112 第9题】
拓展提高
3、已知x≠1,计算:(1+x)(1–x)=1–x2,(1–x)(1+x+x2)=1–x3,
(1–x)(1+x+x2+x3)= 1–x4
(1)观察以上各式并猜想:(1–x)(1+x+x2+…+xn)=________;(n为正整数)
(2)根据你的猜想计算:
①(1–2)(1+2+22+23+24+25)=________;
②2+22+23+…+2n=________(n为正整数);
③(x–1)(x99+x98+x97+…+x2+x+1)=________;
1–xn+1
–63
2n+1–2
x100–1
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
14.2.1平方差公式
人教版八年级上册
教学目标
1、理解并掌握公式的结构特征,会用平方差公式运算。
2、经历探索平方差公式的过程,学会观察、发现规律并归纳、概括,
3、体验数学活动充满着创造性和探索性,并在数学活动中体验成功的喜悦
重点:平方差公式的推导和应用
难点:理解平方差公式的结构特征,灵活运用平方差公式。
复习回顾
多项式与多项式是如何相乘的?
(x + 3)( x+5)
=x2
+5x
+3x
+15
=x2
+8x
+15.
(a+b)(m+n)
=am
+an
+bm
+bn
新知讲解
①(x + 1)( x–1);
②(m + 2)( m–2);
③(2m+ 1)(2m–1);
④(5y + z)(5y–z).
计算下列多项式的积,你能发现什么规律?
做一做
x2 – 12
m2–22
(2m)2 – 12
(5y)2 – z2
这些计算结果有什么特点?
想一想
新知讲解
(a+b)(a b)=
a2 b2
两数和与这两数差的积,等于这两个数的平方差.
公式变形:
1.(a – b ) ( a + b) = a2 – b2
2.(b + a )( –b + a ) = a2 – b2
平方差公式
新知讲解
注:这里的两数可以是两个单项式也可以是两个多项式等.
(a+b)(a–b)=(a)2–(b)2
相同为a
相反为b,–b
适当交换
合理加括号
平方差公式
新知讲解
公式中的a和b,既可以是具体的数,也可以是单项
式或者多项式;
2. 左边是两个二项式的积,并且有一项完全相同,另
一项互为相反数;
3. 右边是相同项的平方减去相反项的绝对值的平方.
(a+b)(a– b)=
a2– b2.
温馨提示
新知讲解
你能根据图1中图形的面积说明平方差公式吗?
思考
新知讲解
方法一:设矩形EBNM的面积+矩形ADFE的面积=S.
S= = .
A
D
F
E
B
N
M
(a-b)b+(a-b)a
a2-b2
新知讲解
方法二:剪下矩形EBNM拼到FBND的位置,如图.
S=S四边形AEBN = .
A
D(M)
N
E
B
N
M
B
(a-b)(a+b)
新知讲解
(1)(3x+2)(3x-2); (2)(-x+2y)(-x-2y).
3x
例 运用平方差公式计算:
(1)中,可以将 看作a,将 看作b,计算结果是 . (2)中,可以将 看作a,将 看作b,计算结果是 .
2
9x2 -4
-x
2y
x2 -4y2
(2) 原式= (–x)2 – (2y)2
= x2 – 4y2.
解: (1)原式=(3x)2–22
=9x2–4;
易错警示:
当相同项带有“负号”时,必须用括号括起来.
强化练习
【课本P108 练习 第1题】
1.下面各式的计算对不对?如果不对,应当怎样改正?
(1)(x+2)(x-2) =x2-2
(2)(-3a-2)(3a-2) =9a2-4
强化练习
运用平方差公式计算:
(1)( x-y)( x+y); (2)(xy+1)(xy-1);
(3)(2a-3b)(3b+2a); (4)(-2b-5)(2b-5);
【课本P112 第1题】
例题讲解
例2 计算:
(1) 102×98; (2) (y+2) (y–2) – (y–1) (y+5) .
= 1002–22
解: (1) 102×98
=10000 – 4
=(100+2)(100–2)
=9996;
= y2–4–y2–4y+5
(2)(y+2)(y–2)– (y–1)(y+5)
= y2–22–(y2+4y–5)
= – 4y + 1.
通过合理变形,利用平方差公式,可以简化运算.
不符合平方差公式运算条件的乘法,按乘法法则进行运算.
强化练习
【课本P108 练习 第2题】
3.运用平方差公式计算:
(1)(a+3b)(a-3b) (2)(3+2a)(-3+2a)
强化练习
【课本P108 练习 第2题】
3.运用平方差公式计算:
(3)51×49 (4)(3x+4)(3x-4) -(2x+3)(3x-2)
例题讲解
例3 对于任意的正整数n,整式(3n+1)(3n–1)–(3–n)(3+n)的值一定是10的整数倍吗?
即(3n+1)(3n–1)–(3–n)(3+n)的值是10的倍数.
解:原式=9n2–1–(9–n2)
=10n2–10.
∵(10n2–10)÷10=n2–1.
n为正整数,
∴n2–1为整数
强化练习
4.如果两个连续奇数分别是2n–1,2n+1(其中n为正整数),证明两个连续奇数的平方差是8的倍数.
证明:(2n+1)2–(2n–1)2
=[(2n+1)+(2n–1)][(2n+1)–(2n–1)]
=(2n+1+2n–1)(2n+1–2n+1)
=4n×2
=8n
因为8n是8的倍数,所以结论成立.
课堂小结
平方差公式
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差.
1.符号表示:(a+b)(a–b)=a2–b2
2.紧紧抓住 “一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式;对于不能直接应用公式的,可能要经过变形才可以应用.
拓展提高
1、先化简,再求值:(x+1)(x–1) +x2(1–x) +x3,其中x=2.
解:原式=x2–1+x2–x3+x3
=2x2–1.
将x=2代入上式,
原式=2×22–1=7.
拓展提高
2、解方程组
(x+2)2-(y-3)2 = (x+y)(x-y),
x-3y = 2.
【课本P112 第9题】
拓展提高
3、已知x≠1,计算:(1+x)(1–x)=1–x2,(1–x)(1+x+x2)=1–x3,
(1–x)(1+x+x2+x3)= 1–x4
(1)观察以上各式并猜想:(1–x)(1+x+x2+…+xn)=________;(n为正整数)
(2)根据你的猜想计算:
①(1–2)(1+2+22+23+24+25)=________;
②2+22+23+…+2n=________(n为正整数);
③(x–1)(x99+x98+x97+…+x2+x+1)=________;
1–xn+1
–63
2n+1–2
x100–1
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
