北师大版八年级数学下册试题 第六章 平行四边形 单元测试卷 (含答案)
文档属性
| 名称 | 北师大版八年级数学下册试题 第六章 平行四边形 单元测试卷 (含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 690.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 00:00:00 | ||
图片预览



文档简介
第六章 《平行四边形》单元测试卷
一、选择题:本题共12个小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.一多边形的每一个内角都等于它相邻外角的4倍,则该多边形的内角和是( )
A.360° B.900° C.1440° D.1800°
2.如图,在平行四边形ABCD中,点E,F分别在AB,CD上,且AE=CF.求证:DE=BF.以下是排乱的证明过程:
①∵AE=CF,∴BE=FD;
②∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD;
③∴DE=BF,
④∴四边形EBFD是平行四边形.
证明步骤正确的顺序是( )
A.①→②→③→④ B.①→④→②→③ C.②→①→④→③ D.②→④→①→③
3.在平面直角坐标系中,以O(0,0)、A(1,1)、B(4,0)为顶点构造平行四边形,下列各点能作为该平行四边形第四个顶点的有( )个.
E(﹣2,1)、F(5,1)、G(1,﹣1)、H(3,﹣1)、I(﹣3,1)
A.2 B.3 C.4 D.5
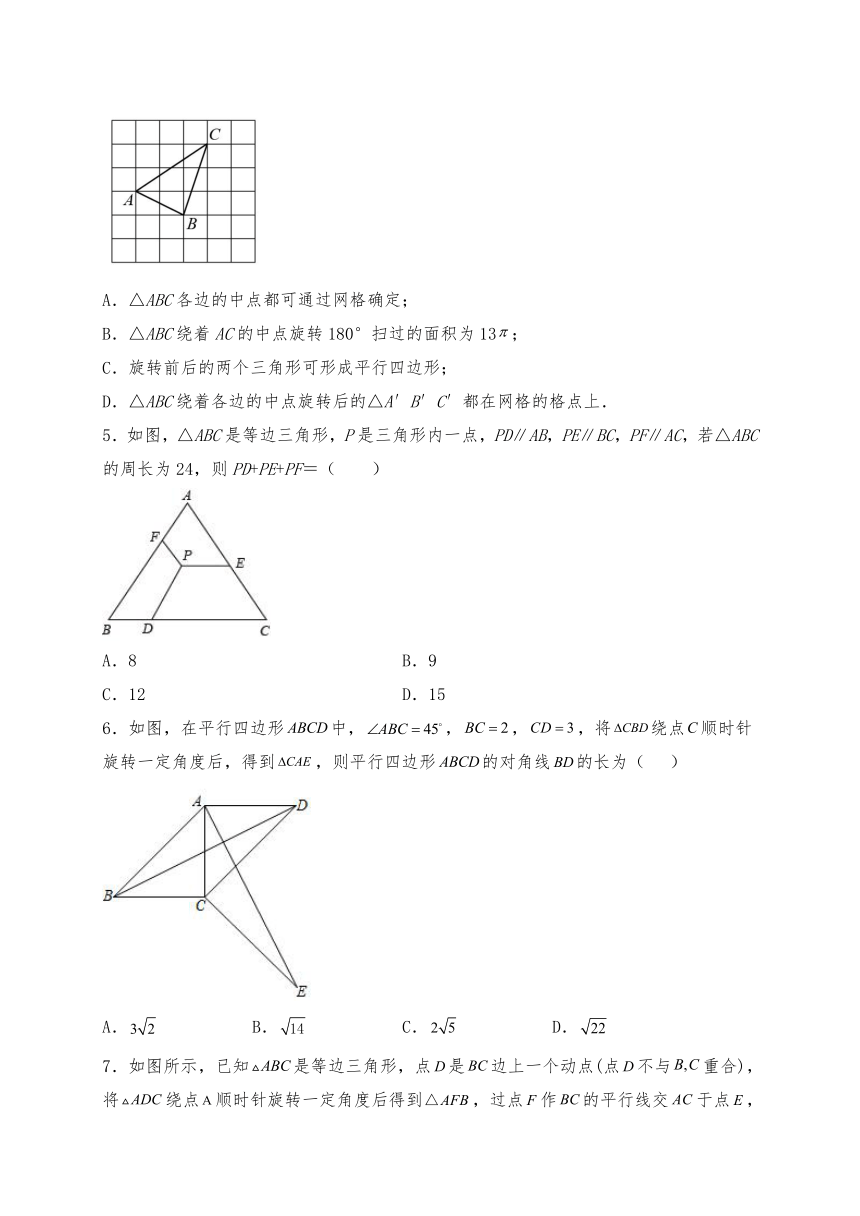
4.如图,是由6×6个边长为1的小正方形网格组成,每个小正方形的顶点称为格点,△ABC的三个顶点A,B,C均在格点上,将△ABC绕着边的中点旋转180°,爱观察与思考的小明发现以下结论不正确是( )
A.△ABC各边的中点都可通过网格确定;
B.△ABC绕着AC的中点旋转180°扫过的面积为13;
C.旋转前后的两个三角形可形成平行四边形;
D.△ABC绕着各边的中点旋转后的△A′B′C′都在网格的格点上.
5.如图,△ABC是等边三角形,P是三角形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为24,则PD+PE+PF=( )
A.8 B.9
C.12 D.15
6.如图,在平行四边形中,,,,将绕点顺时针旋转一定角度后,得到,则平行四边形的对角线的长为( )
A. B. C. D.
7.如图所示,已知是等边三角形,点是边上一个动点(点不与重合),将绕点顺时针旋转一定角度后得到,过点作的平行线交于点,连接,下列四个结论中:①旋转角为;为等边三角形;③四边形为平行四边形;.其中正确的结论有( )
A. B. C. D.
8.如图,平行四边形的边在一次函数的图象上,己知C的坐标是,则过顶点D的正比例函数解析式为( )
A. B. C. D.
9.如图,点E是△ABC内一点,∠AEB=90°,AE平分∠BAC,D是边AB的中点,延长线段DE交边BC于点F,若AB=6,EF=1,则线段AC的长为( )
A.7 B.8 C.9 D.10
10.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=150°;④S四边形AEFD=8.错误的个数是( )
A.1个 B.2个 C.3个 D.4个
11.如图,的周长为19,点,在边上,的角平分线垂直于,垂足为,的角平分线垂直于,垂足为,若,则的长度为( )
A. B.2 C. D.3
12.如图,已知,在平行四边形ABCD中,∠DAB=60°,AB=4,AD=2,把平行四边形沿直线AC折叠,点B落在点E处,连接DE,则DE的长度为( )
A. B. C. D.
二、填空题:本题共6个小题,每小题3分,共18分。
13.如图,的度数为_______.
14.如图,在中,E,F分别在边BC,AD上,有以下条件:①;②;③.若想使四边形AFCE为平行四边形,则还需添加一个条件,这个条件可以是__________(填写相应序号).
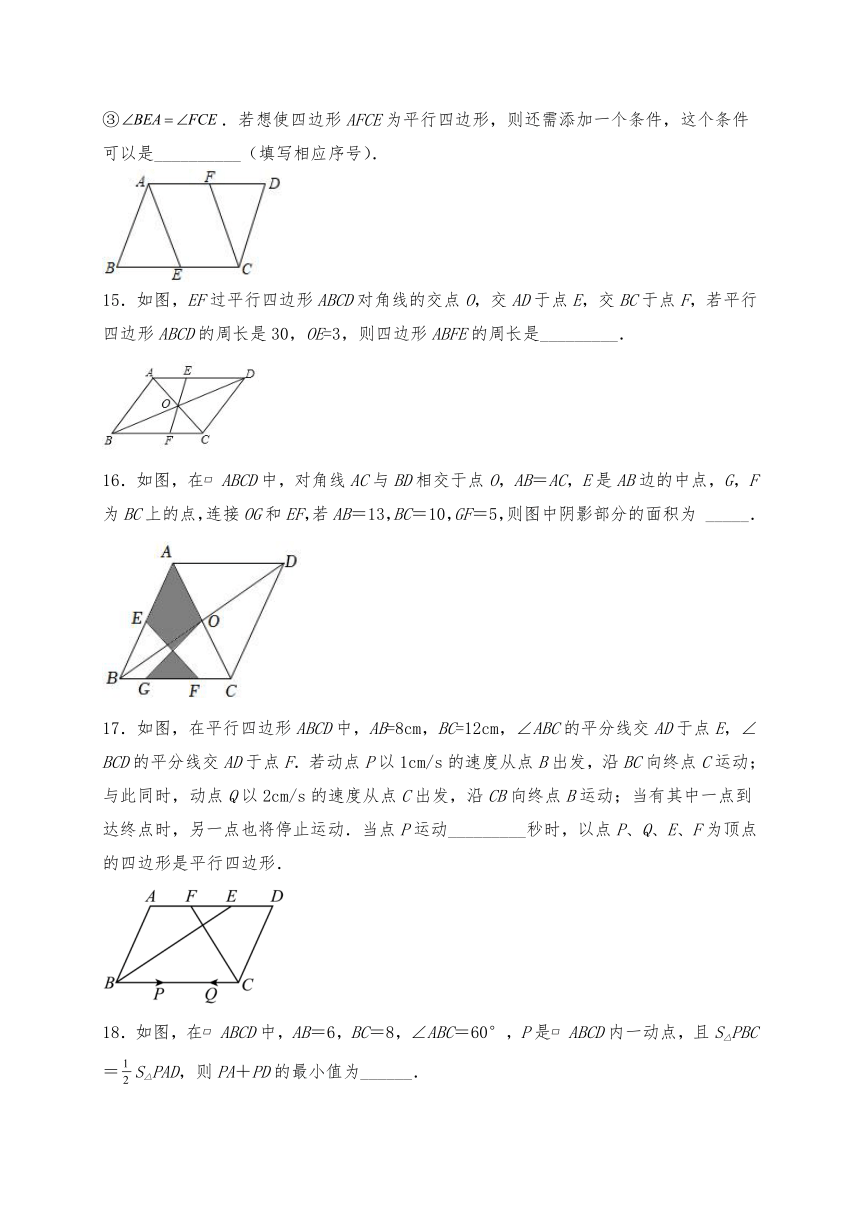
15.如图,EF过平行四边形ABCD对角线的交点O,交AD于点E,交BC于点F,若平行四边形ABCD的周长是30,OE=3,则四边形ABFE的周长是_________.
16.如图,在 ABCD中,对角线AC与BD相交于点O,AB=AC,E是AB边的中点,G,F为BC上的点,连接OG和EF,若AB=13,BC=10,GF=5,则图中阴影部分的面积为 _____.
17.如图,在平行四边形ABCD中,AB=8cm,BC=12cm,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F.若动点P以1cm/s的速度从点B出发,沿BC向终点C运动;与此同时,动点Q以2cm/s的速度从点C出发,沿CB向终点B运动;当有其中一点到达终点时,另一点也将停止运动.当点P运动_________秒时,以点P、Q、E、F为顶点的四边形是平行四边形.
18.如图,在 ABCD中,AB=6,BC=8,∠ABC=60°,P是 ABCD内一动点,且S△PBC=S△PAD,则PA+PD的最小值为______.
三、解答题(19题6分,其余每题8分,共46分)
19.如图,在4×4的方格纸ABCD中,请按要求画格点三角形和格点四边形(顶点在格点上),所画图形的顶点均不与点A,B,C,D重合.
(1)在图1中画一个各边均为无理数的等腰直角△EFG.
(2)在图2中画一个对角线长度之比为:2的平行四边形MNPQ.
20.如图,在平行四边形ABCD中,AB>AD.
(1)尺规作图:在AB上截取AE,使得AE=AD;作∠BCD的平分线交AB于点F.(保留作图痕迹,不写作法)
(2)在(1)所作的图形中,连接DE交CF于点P,求证:△CDP为直角三角形.
(请补全下面的证明过程,不写证明理由)
证明:
∵AE=AD,
∴
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠AED=∠EDC,
∴
∵CF平分∠BCD,
∴
又∵AD∥CB,
∴∠ADC+∠BCD=180°,
∴∠ADC+∠BCD=90°,
∴
∴∠CPD=90°,
∴△CDP是直角三角形.
21.如图1,已知ABCD,∠A=∠BEF=a,E为AD边上一点,F为DC边上一点,BE=EF.
(1)求证:∠ABE=∠DEF
(2)如图1,若a=45°,AE=5, DE=1, 求ABCD的面积;
(3)如图2,若a=30°,AE=4,DE=2.求线段BE的长.
22.已知,如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形.
(2)连结BD交AC于点O,若BD=12,AE=EF-CF,求EG的长.
23.在Rt△ABC中,∠ACB=90°,∠CAB=30°,将△ABC绕点A顺时针旋转一定的角度得到△ADE,点B,C的对应点分别是D,E.
(1)如图1,当点E恰好在AB上时,求∠BDE;
(2)如图2,若=60°,点F是AB中点,求证:四边形CEDF是平行四边形.
24.如图,在平行四边形ABCD中,AB=10,AD=16,∠A=60°,P是射线AD上一点,连接PB,沿PB将△APB折叠,得△A'PB.
(1)如图1所示,当∠DPA'=10°时,∠A'PB= 度;
(2)如图2所示,当PA'⊥BC时,求线段PA的长度;
(3)当点P为AD中点时,点F是边AB上不与点A,B重合的一个动点,将△APF沿PF折叠,得到△A'PF,连接BA',求△BA'F周长的最小值.
答案
一、选择题。
C.C.B.B.A.C.C.C.B.A.C.B.
二、填空题。
13..
14.③.
15.21.
16.30.
17.或.
18..
三、解答题
19.
(1)
如图所示,,△EFG即为所求
(2)
如图所示,平行四边形MNPQ即为所求
20.(1)
解:图形如图所示:
(2)
解:∵AE=AD,
∴∠ADE=∠AED,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠AED=∠EDC,
∴∠ADE=∠CDE,
∵CF平分∠BCD,
∴∠BCF=∠DCF,
又∵AD∥CB,
∴∠ADC+∠BCD=180°,
∴∠ADC+∠BCD=90°,
∴∠CDP+∠DCP=90°,
∴∠CPD=90°,
∴△CDP是直角三角形.
故答案为:∠ADE=∠AED,∠AED=∠EDC,∠BCF=∠DCF,∠CDP+∠DCP=90°.
21.(1)证明:∵∠BED=∠A+∠ABE,∠BED=∠DEF+∠BEF,
∴∠A+∠ABE=∠DEF+∠BEF,
∵∠A=∠BEF,
∴∠ABE=∠DEF;
(2)过E作EH⊥AD交AB于H,
∵∠A= a=45°,∠AEH=90°,AE=5,
∴∠AHE=45°,
∴AH=AE=5,
∵,
∴
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠A+∠D=180°,∠CBG=∠A=45°,
∴∠D=135°=∠EHB,
∵∠ABE=∠DEF,BE=EF,
∴△BEH≌△EFD(AAS),
∴BH=DE=1,
∴AB=AH+BH=,
过点C作CG⊥AB交AB延长线于G,
∵∠CBG=45°,∠G=90°,
∴∠BCG=45°,
∴BG=CG,
∵,BC=AD=6,
∴,
∴ABCD的面积=;
(3)在AB上取点N,连接EN,使EN=AE,过点E作EM⊥AB于M,
∵AE=4,∠A=30°,
∴=2,,
∵EN=AE,EM⊥AB,
∴MN=AM=2,
由(2)得△EBN≌△FED,
∴BN=DE=2,
∴BM=4,
∴.
22.(1)证明:∵四边形ABCD是平行四边形,
∴,AB=CD,
∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,
∴AG=CH,
在△AGE和△CHF中,
∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,
∴,
又∵GE=HF,
∴四边形EGFH是平行四边形;
(2)连接BD交AC于点O,如图,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BD=12,
∴OB=OD=6,
∵AE=CF,OA=OC,
∴OE=OF,
∵AE=EF-CF,
∴AE+CF=EF,AE=CF,
∴2AE=EF=2OE,
∴AE=OE,
又∵点G是AB的中点,
∴EG是△ABO的中位线,
∴.
23.(1)解:△ABC绕点A顺时针旋转一定的角度得到△ADE,点E恰好在AB上,
∴AB=AD,∠EAD=∠CAB=30°,∠DEA=∠BCA=90°,
∵AB=AD,
∴∠ABD=∠ADB=(180° 30°)=75°,
∵∠C=90°,
∴∠ADE=∠ABC=60°,
∴;
(2)连接BD,如图所示:
∵点F是边AB中点,
∴CF=BA,
∵∠BAC=30°,
∴BC=BA,
∴CF=BC,
∵△ABC绕点C顺时针旋转60°得到△ADE,
∴∠CAE=∠BAD=60°,AC=AE,DE=BC,
∴DE=CF,△BAD和△CAE为等边三角形,
∴CE=CA,
∵点F为AB的中点,
∴DF⊥AB,
∴△AFD≌△BCA(AAS),
∴DF=CA,
∴DF=CE,
∵CF=DE,DF=CE,
∴四边形CEDF是平行四边形.
24.
(1)如图1中,
∵∠DPA′=10°,
∴∠APA′=180°﹣∠DPA′=180°﹣10°=170°,
由翻折的性质可知:∠A′PB=∠APB=×170°=85°.
故答案为85.
(2)如图2中,作BH⊥AD于H.
在Rt△ABH中,∵∠AHB=90°,AB=10,∠A=60°,
∴AH=5,BH=5,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵PA′⊥BC,
∴PA′⊥AD,
∴∠APA′=90°,
∴∠HPB=∠BPA′=45°,
∴PH=BH=5,
∴PA=AH+PH=5+5.
(3)如图3中,作BH⊥AD于H,连接BP.
∵PA=8,AH=5,
∴PH=8﹣5=3,
∵BH=5,
∴PB===2,
由翻折可知:PA=PA′=8,FA=FA′,
∴△BFA′的周长=FA′+BF+BA′=AF+BF+BA′=AB+BA′=10+BA′,
∴当BA′的长度最小时,△BFA′的周长最小,
∵BA′≥PB﹣PA′,
∴BA′≥2﹣8,
∴BA′的最小值为2﹣8,
∴△BFA′的周长的最小值为10+2﹣8=2+2.
一、选择题:本题共12个小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.一多边形的每一个内角都等于它相邻外角的4倍,则该多边形的内角和是( )
A.360° B.900° C.1440° D.1800°
2.如图,在平行四边形ABCD中,点E,F分别在AB,CD上,且AE=CF.求证:DE=BF.以下是排乱的证明过程:
①∵AE=CF,∴BE=FD;
②∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD;
③∴DE=BF,
④∴四边形EBFD是平行四边形.
证明步骤正确的顺序是( )
A.①→②→③→④ B.①→④→②→③ C.②→①→④→③ D.②→④→①→③
3.在平面直角坐标系中,以O(0,0)、A(1,1)、B(4,0)为顶点构造平行四边形,下列各点能作为该平行四边形第四个顶点的有( )个.
E(﹣2,1)、F(5,1)、G(1,﹣1)、H(3,﹣1)、I(﹣3,1)
A.2 B.3 C.4 D.5
4.如图,是由6×6个边长为1的小正方形网格组成,每个小正方形的顶点称为格点,△ABC的三个顶点A,B,C均在格点上,将△ABC绕着边的中点旋转180°,爱观察与思考的小明发现以下结论不正确是( )
A.△ABC各边的中点都可通过网格确定;
B.△ABC绕着AC的中点旋转180°扫过的面积为13;
C.旋转前后的两个三角形可形成平行四边形;
D.△ABC绕着各边的中点旋转后的△A′B′C′都在网格的格点上.
5.如图,△ABC是等边三角形,P是三角形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为24,则PD+PE+PF=( )
A.8 B.9
C.12 D.15
6.如图,在平行四边形中,,,,将绕点顺时针旋转一定角度后,得到,则平行四边形的对角线的长为( )
A. B. C. D.
7.如图所示,已知是等边三角形,点是边上一个动点(点不与重合),将绕点顺时针旋转一定角度后得到,过点作的平行线交于点,连接,下列四个结论中:①旋转角为;为等边三角形;③四边形为平行四边形;.其中正确的结论有( )
A. B. C. D.
8.如图,平行四边形的边在一次函数的图象上,己知C的坐标是,则过顶点D的正比例函数解析式为( )
A. B. C. D.
9.如图,点E是△ABC内一点,∠AEB=90°,AE平分∠BAC,D是边AB的中点,延长线段DE交边BC于点F,若AB=6,EF=1,则线段AC的长为( )
A.7 B.8 C.9 D.10
10.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中:①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=150°;④S四边形AEFD=8.错误的个数是( )
A.1个 B.2个 C.3个 D.4个
11.如图,的周长为19,点,在边上,的角平分线垂直于,垂足为,的角平分线垂直于,垂足为,若,则的长度为( )
A. B.2 C. D.3
12.如图,已知,在平行四边形ABCD中,∠DAB=60°,AB=4,AD=2,把平行四边形沿直线AC折叠,点B落在点E处,连接DE,则DE的长度为( )
A. B. C. D.
二、填空题:本题共6个小题,每小题3分,共18分。
13.如图,的度数为_______.
14.如图,在中,E,F分别在边BC,AD上,有以下条件:①;②;③.若想使四边形AFCE为平行四边形,则还需添加一个条件,这个条件可以是__________(填写相应序号).
15.如图,EF过平行四边形ABCD对角线的交点O,交AD于点E,交BC于点F,若平行四边形ABCD的周长是30,OE=3,则四边形ABFE的周长是_________.
16.如图,在 ABCD中,对角线AC与BD相交于点O,AB=AC,E是AB边的中点,G,F为BC上的点,连接OG和EF,若AB=13,BC=10,GF=5,则图中阴影部分的面积为 _____.
17.如图,在平行四边形ABCD中,AB=8cm,BC=12cm,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F.若动点P以1cm/s的速度从点B出发,沿BC向终点C运动;与此同时,动点Q以2cm/s的速度从点C出发,沿CB向终点B运动;当有其中一点到达终点时,另一点也将停止运动.当点P运动_________秒时,以点P、Q、E、F为顶点的四边形是平行四边形.
18.如图,在 ABCD中,AB=6,BC=8,∠ABC=60°,P是 ABCD内一动点,且S△PBC=S△PAD,则PA+PD的最小值为______.
三、解答题(19题6分,其余每题8分,共46分)
19.如图,在4×4的方格纸ABCD中,请按要求画格点三角形和格点四边形(顶点在格点上),所画图形的顶点均不与点A,B,C,D重合.
(1)在图1中画一个各边均为无理数的等腰直角△EFG.
(2)在图2中画一个对角线长度之比为:2的平行四边形MNPQ.
20.如图,在平行四边形ABCD中,AB>AD.
(1)尺规作图:在AB上截取AE,使得AE=AD;作∠BCD的平分线交AB于点F.(保留作图痕迹,不写作法)
(2)在(1)所作的图形中,连接DE交CF于点P,求证:△CDP为直角三角形.
(请补全下面的证明过程,不写证明理由)
证明:
∵AE=AD,
∴
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠AED=∠EDC,
∴
∵CF平分∠BCD,
∴
又∵AD∥CB,
∴∠ADC+∠BCD=180°,
∴∠ADC+∠BCD=90°,
∴
∴∠CPD=90°,
∴△CDP是直角三角形.
21.如图1,已知ABCD,∠A=∠BEF=a,E为AD边上一点,F为DC边上一点,BE=EF.
(1)求证:∠ABE=∠DEF
(2)如图1,若a=45°,AE=5, DE=1, 求ABCD的面积;
(3)如图2,若a=30°,AE=4,DE=2.求线段BE的长.
22.已知,如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形.
(2)连结BD交AC于点O,若BD=12,AE=EF-CF,求EG的长.
23.在Rt△ABC中,∠ACB=90°,∠CAB=30°,将△ABC绕点A顺时针旋转一定的角度得到△ADE,点B,C的对应点分别是D,E.
(1)如图1,当点E恰好在AB上时,求∠BDE;
(2)如图2,若=60°,点F是AB中点,求证:四边形CEDF是平行四边形.
24.如图,在平行四边形ABCD中,AB=10,AD=16,∠A=60°,P是射线AD上一点,连接PB,沿PB将△APB折叠,得△A'PB.
(1)如图1所示,当∠DPA'=10°时,∠A'PB= 度;
(2)如图2所示,当PA'⊥BC时,求线段PA的长度;
(3)当点P为AD中点时,点F是边AB上不与点A,B重合的一个动点,将△APF沿PF折叠,得到△A'PF,连接BA',求△BA'F周长的最小值.
答案
一、选择题。
C.C.B.B.A.C.C.C.B.A.C.B.
二、填空题。
13..
14.③.
15.21.
16.30.
17.或.
18..
三、解答题
19.
(1)
如图所示,,△EFG即为所求
(2)
如图所示,平行四边形MNPQ即为所求
20.(1)
解:图形如图所示:
(2)
解:∵AE=AD,
∴∠ADE=∠AED,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠AED=∠EDC,
∴∠ADE=∠CDE,
∵CF平分∠BCD,
∴∠BCF=∠DCF,
又∵AD∥CB,
∴∠ADC+∠BCD=180°,
∴∠ADC+∠BCD=90°,
∴∠CDP+∠DCP=90°,
∴∠CPD=90°,
∴△CDP是直角三角形.
故答案为:∠ADE=∠AED,∠AED=∠EDC,∠BCF=∠DCF,∠CDP+∠DCP=90°.
21.(1)证明:∵∠BED=∠A+∠ABE,∠BED=∠DEF+∠BEF,
∴∠A+∠ABE=∠DEF+∠BEF,
∵∠A=∠BEF,
∴∠ABE=∠DEF;
(2)过E作EH⊥AD交AB于H,
∵∠A= a=45°,∠AEH=90°,AE=5,
∴∠AHE=45°,
∴AH=AE=5,
∵,
∴
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠A+∠D=180°,∠CBG=∠A=45°,
∴∠D=135°=∠EHB,
∵∠ABE=∠DEF,BE=EF,
∴△BEH≌△EFD(AAS),
∴BH=DE=1,
∴AB=AH+BH=,
过点C作CG⊥AB交AB延长线于G,
∵∠CBG=45°,∠G=90°,
∴∠BCG=45°,
∴BG=CG,
∵,BC=AD=6,
∴,
∴ABCD的面积=;
(3)在AB上取点N,连接EN,使EN=AE,过点E作EM⊥AB于M,
∵AE=4,∠A=30°,
∴=2,,
∵EN=AE,EM⊥AB,
∴MN=AM=2,
由(2)得△EBN≌△FED,
∴BN=DE=2,
∴BM=4,
∴.
22.(1)证明:∵四边形ABCD是平行四边形,
∴,AB=CD,
∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,
∴AG=CH,
在△AGE和△CHF中,
∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,
∴,
又∵GE=HF,
∴四边形EGFH是平行四边形;
(2)连接BD交AC于点O,如图,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BD=12,
∴OB=OD=6,
∵AE=CF,OA=OC,
∴OE=OF,
∵AE=EF-CF,
∴AE+CF=EF,AE=CF,
∴2AE=EF=2OE,
∴AE=OE,
又∵点G是AB的中点,
∴EG是△ABO的中位线,
∴.
23.(1)解:△ABC绕点A顺时针旋转一定的角度得到△ADE,点E恰好在AB上,
∴AB=AD,∠EAD=∠CAB=30°,∠DEA=∠BCA=90°,
∵AB=AD,
∴∠ABD=∠ADB=(180° 30°)=75°,
∵∠C=90°,
∴∠ADE=∠ABC=60°,
∴;
(2)连接BD,如图所示:
∵点F是边AB中点,
∴CF=BA,
∵∠BAC=30°,
∴BC=BA,
∴CF=BC,
∵△ABC绕点C顺时针旋转60°得到△ADE,
∴∠CAE=∠BAD=60°,AC=AE,DE=BC,
∴DE=CF,△BAD和△CAE为等边三角形,
∴CE=CA,
∵点F为AB的中点,
∴DF⊥AB,
∴△AFD≌△BCA(AAS),
∴DF=CA,
∴DF=CE,
∵CF=DE,DF=CE,
∴四边形CEDF是平行四边形.
24.
(1)如图1中,
∵∠DPA′=10°,
∴∠APA′=180°﹣∠DPA′=180°﹣10°=170°,
由翻折的性质可知:∠A′PB=∠APB=×170°=85°.
故答案为85.
(2)如图2中,作BH⊥AD于H.
在Rt△ABH中,∵∠AHB=90°,AB=10,∠A=60°,
∴AH=5,BH=5,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵PA′⊥BC,
∴PA′⊥AD,
∴∠APA′=90°,
∴∠HPB=∠BPA′=45°,
∴PH=BH=5,
∴PA=AH+PH=5+5.
(3)如图3中,作BH⊥AD于H,连接BP.
∵PA=8,AH=5,
∴PH=8﹣5=3,
∵BH=5,
∴PB===2,
由翻折可知:PA=PA′=8,FA=FA′,
∴△BFA′的周长=FA′+BF+BA′=AF+BF+BA′=AB+BA′=10+BA′,
∴当BA′的长度最小时,△BFA′的周长最小,
∵BA′≥PB﹣PA′,
∴BA′≥2﹣8,
∴BA′的最小值为2﹣8,
∴△BFA′的周长的最小值为10+2﹣8=2+2.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
