北师大版八年级数学下册试题 第六章 平行四边形 复习卷 (含答案)
文档属性
| 名称 | 北师大版八年级数学下册试题 第六章 平行四边形 复习卷 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 452.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 09:38:21 | ||
图片预览



文档简介
第六章《平行四边形》复习卷
一、选择题。
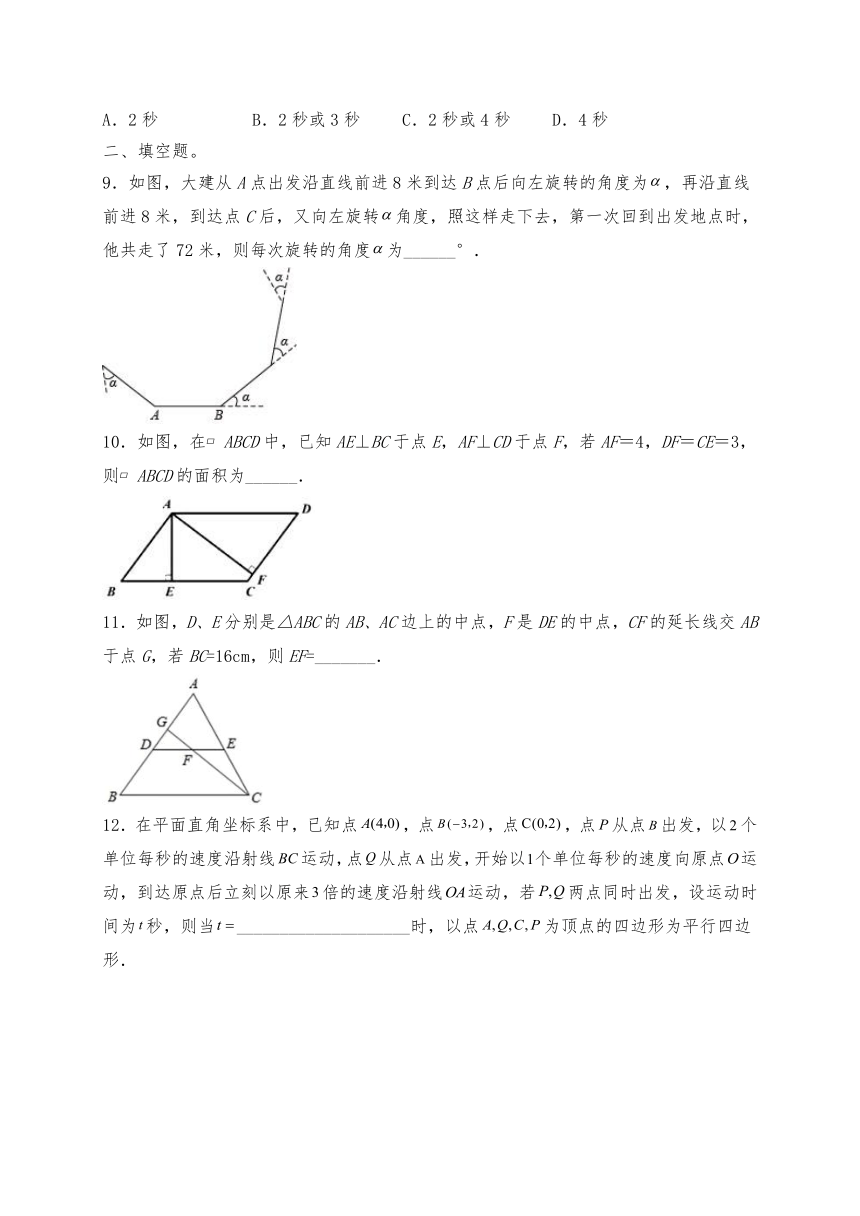
1.如图,时钟外框造型是正八边形,其内角和是( )
A. B. C. D.
2.已知一个凸四边形的一条对角线被另一条对角线平分,请你从下列四个条件中再选取一个作为已知条件,使得这个四边形一定是平行四边形.你的选择是( )
A.一组对边平行; B.一组对角相等; C.一组邻边相等; D.一组对边相等.
3.如图,,,是五边形的3个外角,若,则等于( )
A.130° B.180° C.230° D.330°
4.如图,四边形ABCD四边的中点分别为E,F,G,H,对角线AC与BD相交于点O,若四边形EFGH的周长是3,则AC+BD的长为( )
A.3 B.6 C.9 D.12
5.如图,在 中,∠ABD=25°,现将 沿 EF 折叠,使点 B 与点 D 重合,点 C 落在点 G 处, 若 G 在 AD 延长线上,则∠GDF 的度数是( )
A.45° B.50° C.60° D.65°
6.如图所示,在中,垂直平分于,其中,,则的对角线的长为( )
A. B. C. D.12
7.已知是边长为10的等边三角形,为的中点,,交线段于,交的延长线于.若,则的长为( )
A.1 B.2 C.3 D.4
8.如图,在四边形中,,,,点在边上以每秒的速度从点向点运动,点在边上,以每秒的速度从点向点运动,当直线在四边形内部截出一个平行四边形时,点运动了( )
A.2秒 B.2秒或3秒 C.2秒或4秒 D.4秒
二、填空题。
9.如图,大建从A点出发沿直线前进8米到达B点后向左旋转的角度为,再沿直线前进8米,到达点C后,又向左旋转角度,照这样走下去,第一次回到出发地点时,他共走了72米,则每次旋转的角度为______°.
10.如图,在 ABCD中,已知AE⊥BC于点E,AF⊥CD于点F,若AF=4,DF=CE=3,则 ABCD的面积为______.
11.如图,D、E分别是△ABC的AB、AC边上的中点,F是DE的中点,CF的延长线交AB于点G,若BC=16cm,则EF=_______.
12.在平面直角坐标系中,已知点,点,点,点从点出发,以个单位每秒的速度沿射线运动,点从点出发,开始以个单位每秒的速度向原点运动,到达原点后立刻以原来倍的速度沿射线运动,若两点同时出发,设运动时间为秒,则当____________________时,以点为顶点的四边形为平行四边形.
三、解答题。
13.如图,已知CD为△ABC中线,E为CD上一点,连接AE并延长至点F,使,连接BF、CF,.
(1)求证:四边形DBFC是平行四边形.
(2)设四边形ABFC的面积为S,在不添加任何辅助线的情况下,请写出图中四个面积等于的三角形.
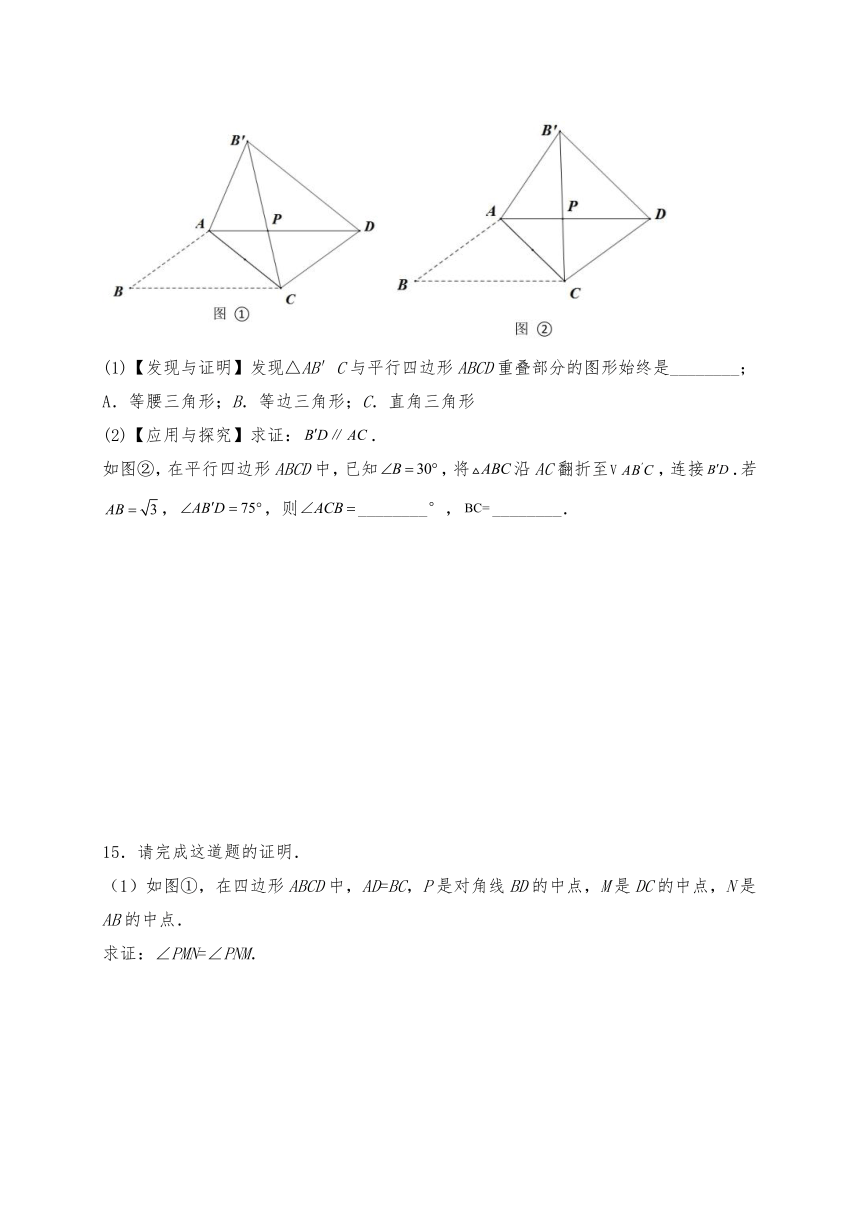
14.数学兴趣小组在学习平行四边形的性质后,开始进一步的探索.他们将平行四边形沿着它的一条对角线翻折,发现其中还有很多结论:如图①,在平行四边形ABCD中,,将沿AC翻折至,连接.
(1)【发现与证明】发现△AB′C与平行四边形ABCD重叠部分的图形始终是________;
A.等腰三角形;B.等边三角形;C.直角三角形
(2)【应用与探究】求证:.
如图②,在平行四边形ABCD中,已知,将沿AC翻折至,连接.若,,则________°,________.
15.请完成这道题的证明.
(1)如图①,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.
求证:∠PMN=∠PNM.
【知识延伸】
(2)如图②,延长图①中的线段AD交NM的延长线于点E,延长线段BC交NM的延长线于点F,求证:∠AEN=∠F.
【应用探究】
(3)如图③,在△ABC中,AC<AB,D点在AC上,AD=BC,M是DC的中点,N是AB的中点,连接NM并延长,与BC的延长线交于点G,若∠AMN=60°,连接GD,则△CGD形状是__________________________.
答案
一、选择题。
C.A.C.A.D.A.C.B.
二、填空题。
9.40.
10..
11.4cm.
12.1或3或13
三、解答题。
13.
(1)
证明:∵,
∴∠DAE=∠CFE,
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS)
∴AD=FC,
∵CD为△ABC中线,
∴AD=BD=CF,
∵BD∥FC,
所以四边形DBFC为平行四边形;
(2)
∵CD为△ACB的中线,
∴S△ACD=S△BCD,
∵BC为平行四边形DBFC的对角线,
∴S△DBC=S△FBC,
∵△ACF与△BCF为同底等高的三角形,
∴S△BCF=S△AFC,
∵S四边形ABFC=S△ADC+S△BDC+S△BFC=3S△ADC,
∴S△ADC=,
∴S△BCF=S△AFC= S△BCD= S△ACD=.
14.
(1)
解:△AB′C与 ABCD重叠部分的图形是等腰三角形;
证明:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,∠B=∠ADC,
∵将△ABC沿AC翻折至△AB′C,
∴AB′=AB,B′C=BC,∠AB′C=∠B,
∴AB′=CD,B′C=AD,∠AB′C=∠ADC,
在△AB′C和△CDA中,
,
∴△AB′C≌△CDA(SAS),
∴∠ACB′=∠CAD,
设AD、B′C相交于P,
∴AP=CP,
∴△ACP是等腰三角形,
即△AB′C与 ABCD重叠部分的图形是等腰三角形;
(2)证明:由(1)得:B′C=AD,AP=CP,
∴B′P=DP,
∴∠CB′D=∠ADB′,
∵∠APC=∠B′PD,∠ACB′=∠CAD,
∴∠ADB′=∠DAC,
∴B′D∥AC;
如图中,
∵在 ABCD中,∠B=30°,将△ABC沿AC翻折至△AB′C,
∴∠AB′C=30°,
∵∠AB′D=75°,
∴∠CB′D=45°,
∵B′D∥AC,
∴∠ACB′=∠CB′D=45°,
∵∠ACB=∠ACB′,
∴∠ACB=45°;
作AG⊥BC于G,
∴AG=CG,
∵∠B=30°,
∴AG=AB=×=,
∴CG=AG=,BG=,
∴BC=BG+CG=.
15.
(1)证明:∵P是BD的中点,M是DC的中点,
∴PM是△BCD的中位线,PN是△ABD的中位线,
∴PM=BC,PN=AD,
∵AD=BC,
∴PM=PN,
∴∠PMN=∠PNM;
(2)证明:由(1)知,PM是△BDC的中位线,PN是△ABD的中位线,
∴PM∥BC,PN∥AD,
∴∠PMN=∠F,∠PNM=∠AEN,
∵∠PMN=∠PNM,
∴∠AEN=∠F;
(3)解:△CGD是直角三角形,理由如下:
如图③,连接BD,取BD的中点P,连接PM、PN,
∵M是CD的中点,N是AB的中点,
∴PM是△BCD的中位线,PN是△ABD的中位线,
∴PM∥BC,PM=BC,PN∥AD,PN=AD,
∵AD=BC,
∴PM=PN,
∴∠PNM=∠PMN,
∵PN∥AD,
∴∠PNM=∠AMN=60°,
∴∠PNM=∠PMN=60°,
∵PM∥BC,
∴∠CGM=∠PMN=60°,
又∵∠CMG=∠AMN=60°,
∴△CGM是等边三角形.
∴CM=GM,
又∵CM=DM,
∴DM=GM,
∴∠MDG=∠MGD=∠CMG=30°,
∴∠CGD=∠CGM+∠MGD=90°,
∴△CGD是直角三角形,
故答案为:直角三角形.
一、选择题。
1.如图,时钟外框造型是正八边形,其内角和是( )
A. B. C. D.
2.已知一个凸四边形的一条对角线被另一条对角线平分,请你从下列四个条件中再选取一个作为已知条件,使得这个四边形一定是平行四边形.你的选择是( )
A.一组对边平行; B.一组对角相等; C.一组邻边相等; D.一组对边相等.
3.如图,,,是五边形的3个外角,若,则等于( )
A.130° B.180° C.230° D.330°
4.如图,四边形ABCD四边的中点分别为E,F,G,H,对角线AC与BD相交于点O,若四边形EFGH的周长是3,则AC+BD的长为( )
A.3 B.6 C.9 D.12
5.如图,在 中,∠ABD=25°,现将 沿 EF 折叠,使点 B 与点 D 重合,点 C 落在点 G 处, 若 G 在 AD 延长线上,则∠GDF 的度数是( )
A.45° B.50° C.60° D.65°
6.如图所示,在中,垂直平分于,其中,,则的对角线的长为( )
A. B. C. D.12
7.已知是边长为10的等边三角形,为的中点,,交线段于,交的延长线于.若,则的长为( )
A.1 B.2 C.3 D.4
8.如图,在四边形中,,,,点在边上以每秒的速度从点向点运动,点在边上,以每秒的速度从点向点运动,当直线在四边形内部截出一个平行四边形时,点运动了( )
A.2秒 B.2秒或3秒 C.2秒或4秒 D.4秒
二、填空题。
9.如图,大建从A点出发沿直线前进8米到达B点后向左旋转的角度为,再沿直线前进8米,到达点C后,又向左旋转角度,照这样走下去,第一次回到出发地点时,他共走了72米,则每次旋转的角度为______°.
10.如图,在 ABCD中,已知AE⊥BC于点E,AF⊥CD于点F,若AF=4,DF=CE=3,则 ABCD的面积为______.
11.如图,D、E分别是△ABC的AB、AC边上的中点,F是DE的中点,CF的延长线交AB于点G,若BC=16cm,则EF=_______.
12.在平面直角坐标系中,已知点,点,点,点从点出发,以个单位每秒的速度沿射线运动,点从点出发,开始以个单位每秒的速度向原点运动,到达原点后立刻以原来倍的速度沿射线运动,若两点同时出发,设运动时间为秒,则当____________________时,以点为顶点的四边形为平行四边形.
三、解答题。
13.如图,已知CD为△ABC中线,E为CD上一点,连接AE并延长至点F,使,连接BF、CF,.
(1)求证:四边形DBFC是平行四边形.
(2)设四边形ABFC的面积为S,在不添加任何辅助线的情况下,请写出图中四个面积等于的三角形.
14.数学兴趣小组在学习平行四边形的性质后,开始进一步的探索.他们将平行四边形沿着它的一条对角线翻折,发现其中还有很多结论:如图①,在平行四边形ABCD中,,将沿AC翻折至,连接.
(1)【发现与证明】发现△AB′C与平行四边形ABCD重叠部分的图形始终是________;
A.等腰三角形;B.等边三角形;C.直角三角形
(2)【应用与探究】求证:.
如图②,在平行四边形ABCD中,已知,将沿AC翻折至,连接.若,,则________°,________.
15.请完成这道题的证明.
(1)如图①,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.
求证:∠PMN=∠PNM.
【知识延伸】
(2)如图②,延长图①中的线段AD交NM的延长线于点E,延长线段BC交NM的延长线于点F,求证:∠AEN=∠F.
【应用探究】
(3)如图③,在△ABC中,AC<AB,D点在AC上,AD=BC,M是DC的中点,N是AB的中点,连接NM并延长,与BC的延长线交于点G,若∠AMN=60°,连接GD,则△CGD形状是__________________________.
答案
一、选择题。
C.A.C.A.D.A.C.B.
二、填空题。
9.40.
10..
11.4cm.
12.1或3或13
三、解答题。
13.
(1)
证明:∵,
∴∠DAE=∠CFE,
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS)
∴AD=FC,
∵CD为△ABC中线,
∴AD=BD=CF,
∵BD∥FC,
所以四边形DBFC为平行四边形;
(2)
∵CD为△ACB的中线,
∴S△ACD=S△BCD,
∵BC为平行四边形DBFC的对角线,
∴S△DBC=S△FBC,
∵△ACF与△BCF为同底等高的三角形,
∴S△BCF=S△AFC,
∵S四边形ABFC=S△ADC+S△BDC+S△BFC=3S△ADC,
∴S△ADC=,
∴S△BCF=S△AFC= S△BCD= S△ACD=.
14.
(1)
解:△AB′C与 ABCD重叠部分的图形是等腰三角形;
证明:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,∠B=∠ADC,
∵将△ABC沿AC翻折至△AB′C,
∴AB′=AB,B′C=BC,∠AB′C=∠B,
∴AB′=CD,B′C=AD,∠AB′C=∠ADC,
在△AB′C和△CDA中,
,
∴△AB′C≌△CDA(SAS),
∴∠ACB′=∠CAD,
设AD、B′C相交于P,
∴AP=CP,
∴△ACP是等腰三角形,
即△AB′C与 ABCD重叠部分的图形是等腰三角形;
(2)证明:由(1)得:B′C=AD,AP=CP,
∴B′P=DP,
∴∠CB′D=∠ADB′,
∵∠APC=∠B′PD,∠ACB′=∠CAD,
∴∠ADB′=∠DAC,
∴B′D∥AC;
如图中,
∵在 ABCD中,∠B=30°,将△ABC沿AC翻折至△AB′C,
∴∠AB′C=30°,
∵∠AB′D=75°,
∴∠CB′D=45°,
∵B′D∥AC,
∴∠ACB′=∠CB′D=45°,
∵∠ACB=∠ACB′,
∴∠ACB=45°;
作AG⊥BC于G,
∴AG=CG,
∵∠B=30°,
∴AG=AB=×=,
∴CG=AG=,BG=,
∴BC=BG+CG=.
15.
(1)证明:∵P是BD的中点,M是DC的中点,
∴PM是△BCD的中位线,PN是△ABD的中位线,
∴PM=BC,PN=AD,
∵AD=BC,
∴PM=PN,
∴∠PMN=∠PNM;
(2)证明:由(1)知,PM是△BDC的中位线,PN是△ABD的中位线,
∴PM∥BC,PN∥AD,
∴∠PMN=∠F,∠PNM=∠AEN,
∵∠PMN=∠PNM,
∴∠AEN=∠F;
(3)解:△CGD是直角三角形,理由如下:
如图③,连接BD,取BD的中点P,连接PM、PN,
∵M是CD的中点,N是AB的中点,
∴PM是△BCD的中位线,PN是△ABD的中位线,
∴PM∥BC,PM=BC,PN∥AD,PN=AD,
∵AD=BC,
∴PM=PN,
∴∠PNM=∠PMN,
∵PN∥AD,
∴∠PNM=∠AMN=60°,
∴∠PNM=∠PMN=60°,
∵PM∥BC,
∴∠CGM=∠PMN=60°,
又∵∠CMG=∠AMN=60°,
∴△CGM是等边三角形.
∴CM=GM,
又∵CM=DM,
∴DM=GM,
∴∠MDG=∠MGD=∠CMG=30°,
∴∠CGD=∠CGM+∠MGD=90°,
∴△CGD是直角三角形,
故答案为:直角三角形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
