北师大版九年级数学下册试题 第三章 圆 单元测试卷(含答案)
文档属性
| 名称 | 北师大版九年级数学下册试题 第三章 圆 单元测试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 715.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 00:00:00 | ||
图片预览



文档简介
第三章 《圆》单元测试卷
一、选择题:本题共12个小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列说法中,正确的是( )
A.等弦所对的弧相等 B.等弧所对的弦相等
C.圆心角相等,所对的弦相等 D.弦相等所对的圆心角相等
2.如图,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若弧CE的度数是92°,则∠C的度数是( )
A.46° B.88° C.24° D.23°
3.如图,根据下列尺规作图痕迹,其中表示点O是△ABC外心的是( )
A. B.
C. D.
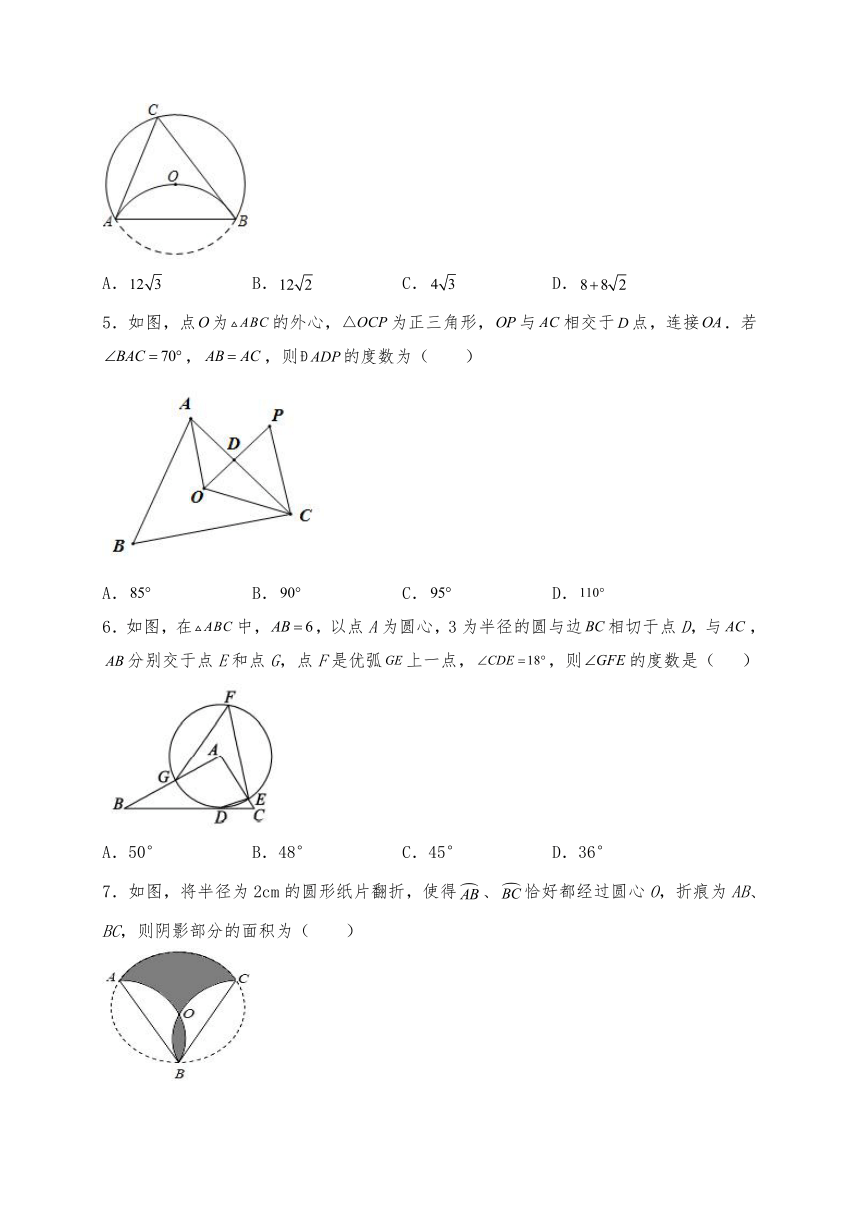
4.如图,的半径为,将劣弧沿弦翻折,恰好经过圆心,点为优弧上的一个动点,则面积的最大值是( )
A. B. C. D.
5.如图,点为的外心,为正三角形,与相交于点,连接.若,,则的度数为( )
A. B. C. D.
6.如图,在中,,以点A为圆心,3为半径的圆与边相切于点D,与,分别交于点E和点G,点F是优弧上一点,,则的度数是( )
A.50° B.48° C.45° D.36°
7.如图,将半径为2cm的圆形纸片翻折,使得、恰好都经过圆心O,折痕为AB、BC,则阴影部分的面积为( )
A.πcm2 B.πcm2 C.πcm2 D.πcm2
8.如图,将边长为的正六边形在直线l上由图的位置按顺时针方向向右作无滑动滚动,当正六边形旋转一周滚动到图位置时,顶点所经过的路径( )
A. B. C. D.
9.如图,有一圆锥形粮堆,其侧面展开图是半径为6m的半圆,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程长为( )
A.3m B.m C.m D.4m
10.如图,AB是半圆O的直径,小宇按以下步骤作图:
(1)分别以A、B为圆心,大于AO长为半径作弧,两弧交于P点,连接OP与半圆交于C点;
(2)分别以A、C为圆心,大于AC长为半径作弧,两弧交于Q点,连接OQ与半圆交于D点;
(3)连接AD、BD、BC,BD与OC交于E点.
根据以上作图过程及所作图形,下轮结论:①BD平分∠ABC;②BC∥OD;③CE=OE.所有正确结论的序号是( )
A.①② B.②③ C.①③ D.①②③
11.如图,I为的内心,有一直线通过I点且分别与AB、AC相交于D点、E点若,,则I点到BC的距离为何?( )
A. B. C.2 D.3
12.如图,在正方形ABCD中,以BC为直径作半圆O,以D为圆心,DA为半径作,与半圆O交于点P,我们称:点P为正方形ABCD的一个“奇妙点”,过奇妙点的多条线段与正方形ABCD无论是位置关系还是数量关系,都具有不少优美的性质值得探究.连接PA、PB、PC、PD,并延长PD交AB于点F.下列结论中:①FD=FB+BC;②∠APC=135°;③S△PBC=AP2;④tan∠BAP=;其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
二、填空题:本题共6个小题,每小题3分,共18分。
13.矩形ABCD中,边AB=6cm,AD=8cm,以A为圆心作⊙A,使B、C、D三点有两个点在⊙A内有一点在⊙A外,则⊙A的半径r的取值范围是____.
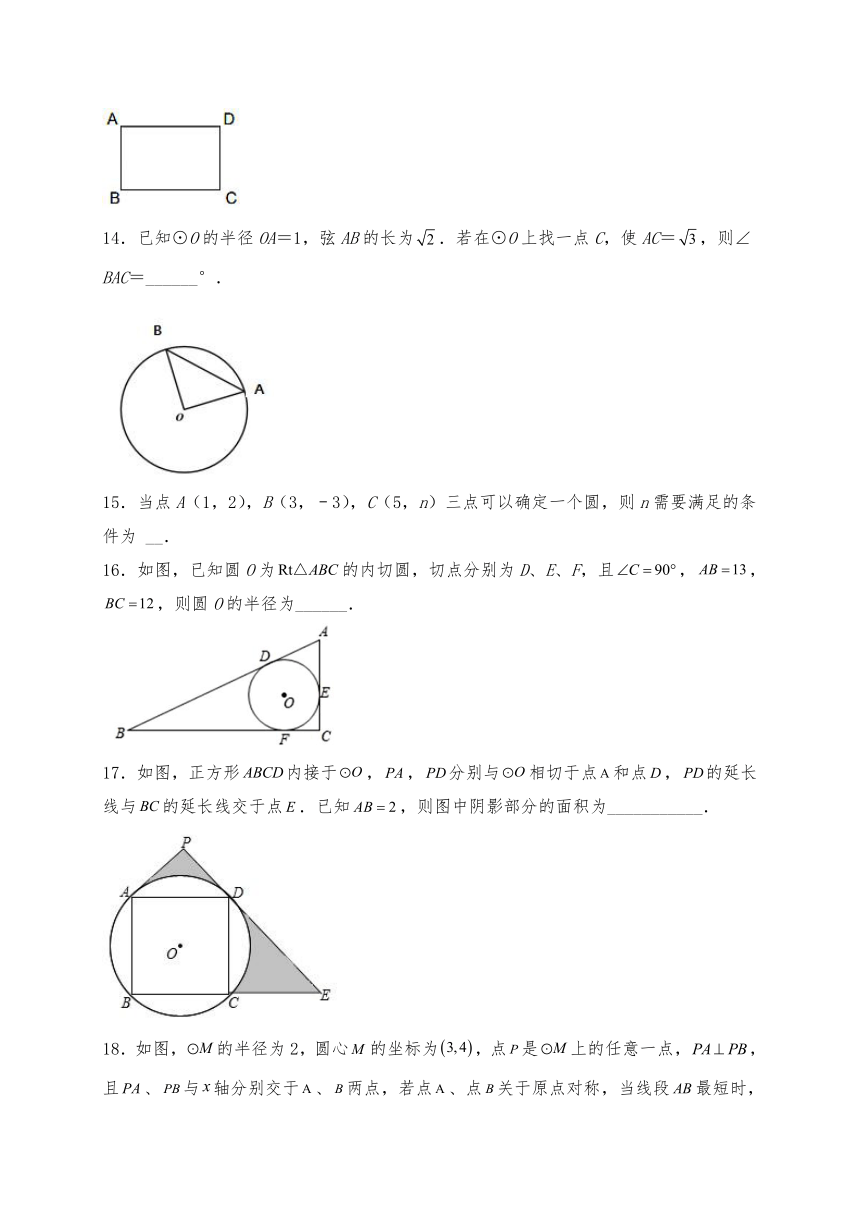
14.已知⊙O的半径OA=1,弦AB的长为.若在⊙O上找一点C,使AC=,则∠BAC=______°.
15.当点A(1,2),B(3,﹣3),C(5,n)三点可以确定一个圆,则n需要满足的条件为 __.
16.如图,已知圆O为的内切圆,切点分别为D、E、F,且,,,则圆O的半径为______.
17.如图,正方形内接于,,分别与相切于点和点,的延长线与的延长线交于点.已知,则图中阴影部分的面积为___________.
18.如图,的半径为2,圆心的坐标为,点是上的任意一点,,且、与轴分别交于、两点,若点、点关于原点对称,当线段最短时,点的坐标为______.
三、解答题(19题6分,其余每题8分,共46分)
19.如图所示,在平面直角坐标系中,⊙P经过原点,交x轴于点A(4,0),交y轴于点B(0,3),点C是劣弧OA的中点,连接BC.
(1)求⊙P的半径
(2)求弦BC的长
20.如图,四边形ABCD为⊙O的内接四边形,BD=BC,BA、CD延长线交于点E.
(1)求证:∠EAD=∠BAC;
(2)若的度数为64°,则∠E的度数为 °.
21.如图,的半径OC垂直于弦AB,垂足为D.
(1)若,,求;
(2)若,,求AB的长.
(3)若BC平分,判断直线BE与的位置关系,并加以证明.
22.如图1,扇形的半径为4,圆心角为,点为上任意一点(不与点,重合),且于点,点为的内心,连接,,.
(1)求的度数;
(2)如图2,⊙为的外接圆,点在上运动.
①当时,判断与⊙的位置关系,并加以证明;
②设⊙的半径为,若的值不随点的运动而改变,请直接写出的值;若随着点的运动而在一个范围内变化,请直接写出这个变化范围.
23.如图,有一个直径MN=4的半圆形纸片,其圆心为点P,从初始阶段Ⅰ位置开始,在无滑动的情况下沿数轴向右翻滚至位置Ⅴ,其中位置Ⅰ中的MN平行于数轴,且半⊙P与数轴相切于原点O;位置Ⅱ和位置Ⅳ中MN的垂直于数轴;位置Ⅲ中的MN在数轴上;位置Ⅴ中的点N到数轴的距离为3,且半⊙P与数轴相切于点A.解答下列问题:
(1)位置Ⅰ中MN的与数轴之间的距离为 ;位置Ⅱ中的半⊙P与数轴位置关系是 ;
(2)求位置Ⅲ中的圆心P在数轴上表示的数;
(3)纸片半⊙P从位置Ⅲ翻滚到位置Ⅳ时,求点N所经过路径长及该纸片所扫过的图形的面积;
(4)求OA的长,(结果保留)
24.如图,在中,,,,动点从点出发,沿着方向以1个单位长度/秒的速度匀速运动,同时动点从点方向出发,沿着方向也以1个单位长度/秒的速度匀速运动,设运动时间为秒,以为圆心,长为半径的与、的另一个交点分别为、,连接、.
(1)当点与点重合时,求的值;
(2)若是等腰三角形,求的值;
(3)若与线段只有一个公共点,求的取值范围.
答案
一、选择题。
B.D.C.A.A.B.C.B.C.D.A.A.
二、填空题。
13.8cm14.15°或75°
15.n≠﹣8.
16.2
17.5-π.
18..
三、解答题
19.
(1)解:∵⊙P过原点O,与x轴交于A(4,0),与y轴交于B(0,3),
∴AB是⊙O的直径,AO=4,BO=3,
由题意可得出:OA2+OB2=AB2,
∴AB=5,
∴⊙P的半径为;
(2)连接PC交OA于点H,连接AC,
∵点C是劣弧OA的中点,
∴OH=AH==2,PH⊥OA,
∵PA=,
∴PH==,
∴CH=PC-PH=-=1,
∴AC=,
∵AB为⊙P的直径,
∴∠ACB=90°,
∴BC==2.
20.
(1)证明:∵四边形ABCD为⊙O的内接四边形,
∴∠BAD+∠BCD=180°,
∵∠BAD+∠EAD=180°,
∴∠EAD=∠BCD,
∵BD=BC,
∴∠BDC=∠BCD,
由圆周角定理得:∠BAC=∠BDC=∠BCD,
∴∠EAD=∠BAC;
(2)解:∵的度数为64°,
∴∠ACB=32°,
∵四边形ABCD为⊙O的内接四边形,
∴∠EDA=∠ABC,
∵∠EAD=∠BAC,
∴∠E=180°-∠EAD-∠EDA=180°-∠BAC-∠ABC=∠ACB,
∴∠E=∠ACB=32°,
故答案为:32.
21.
(1)∵半径OC垂直于弦AB,
∴,
在中,,,
∴根据勾股定理,得,
∴,
在中,,,
∴;
(2)∵,
,
∵,
∴,
在中,,
∵半径OC垂直于弦AB,
∴;
(3)BE与相切.
证明如下:
如图所示,连接,∵平分,
∴,
∵,
∴,
∵,
∴,
∵半径垂直于弦,
∴,
∴,
∴.
∵是的半径,
∴为的切线.
22.
解:(1)∵点为的内心,
∴.
又∵,,
∴.
∵于点,
∴.
∴.
∴.
∴.
(2)①当时,与相切.
证明如下:
如图,在优弧上取一点,连接,.
∵点在劣弧上,且,
∴.
∴.
连接,.
∴.
∴.
而当时,
,
∴.
∴当时,与相切.
②的值是定值;.理由如下:
当点C在上运动时,由(2)证得,OM=MB=r,△OBM为等腰直角三角形,而OB=4,故OM=MB=.
23.
解:(1)位置Ⅰ中的MN平行于数轴,则与数轴的距离为半径2,
位置Ⅱ和位置Ⅳ中MN的垂直于数轴,
可判断位置Ⅱ中的半⊙P与数轴位置关系相切,
故答案为:2,相切;
(2)从位置Ⅰ到位置Ⅱ,的长等于数轴上的长,从位置Ⅱ到位置Ⅲ,数轴上的,故数轴上的,
,
位置Ⅲ中的圆心P在数轴上表示的数为;
(3)点N所经过路径长为,
S半圆=,S扇形=,
半⊙P所扫过图形的面积为2π+4π=6π;
(4)如图,作NC垂直数轴于点C,作PH⊥NC于点H,连接PA,
则四边形PHCA为矩形,
在Rt△NPH中,PN=2,NH=NC-HC=NC-PA=1,
于是sin∠NPH=,
∴∠NPH=30°,
∴∠MPA=60°,
从而的长为,
于是OA的长为.
24.
解:(1)∵OA=6,OB=8,
∴由勾股定理可求得:AB=10,
由题意知:OQ=AP=t,
∴AC=2t,
∵AC是⊙P的直径,
∴∠CDA=90°,
∴CD∥OB,
∴△ACD∽△ABO,
∴,
∴AD=,
当Q与D重合时,
AD+OQ=OA,
∴+t=6,
∴t=;
(2)若△ACQ是等腰三角形时,分三种情况讨论:
①当AQ=AC时,即AC=AQ=2t,OQ=t,
∵OQ+QA=6,
∴t+2t=6,
解得t=2;
②当QC=CA时,即QC=CA=2t,由(1)知DA=,
∴QD=DA=,
∴OQ+QD+DA=6,
∴,
解得:;
③当QC=QA时,如图,连接PQ,
可知PQ⊥AC,
∴∠QPA=∠BOA=90°,∠QAP=∠BAO,
∴△AQE∽△ABO,
则AE=t,AQ=6-t,
∴,
∴,
解得:;
综上所述,当△ACQ是等腰三角形时,t=2或或;
(3)当QC与⊙P相切时,如图
此时∠QCA=90°,
∵OQ=AP=t,
∴AQ=6﹣t,AC=2t,
∵∠A=∠A,
∠QCA=∠ABO,
∴△AQC∽△ABO,
∴,
∴,
∴t=,
∴当0<t≤时,⊙P与QC只有一个交点,
当QC⊥OA时,
此时Q与D重合,
由(1)可知:t=,
∴当<t≤5时,⊙P与QC只有一个交点,
综上所述,当,⊙P与QC只有一个交点,t的取值范围为:0<t≤或<t≤5.
一、选择题:本题共12个小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列说法中,正确的是( )
A.等弦所对的弧相等 B.等弧所对的弦相等
C.圆心角相等,所对的弦相等 D.弦相等所对的圆心角相等
2.如图,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若弧CE的度数是92°,则∠C的度数是( )
A.46° B.88° C.24° D.23°
3.如图,根据下列尺规作图痕迹,其中表示点O是△ABC外心的是( )
A. B.
C. D.
4.如图,的半径为,将劣弧沿弦翻折,恰好经过圆心,点为优弧上的一个动点,则面积的最大值是( )
A. B. C. D.
5.如图,点为的外心,为正三角形,与相交于点,连接.若,,则的度数为( )
A. B. C. D.
6.如图,在中,,以点A为圆心,3为半径的圆与边相切于点D,与,分别交于点E和点G,点F是优弧上一点,,则的度数是( )
A.50° B.48° C.45° D.36°
7.如图,将半径为2cm的圆形纸片翻折,使得、恰好都经过圆心O,折痕为AB、BC,则阴影部分的面积为( )
A.πcm2 B.πcm2 C.πcm2 D.πcm2
8.如图,将边长为的正六边形在直线l上由图的位置按顺时针方向向右作无滑动滚动,当正六边形旋转一周滚动到图位置时,顶点所经过的路径( )
A. B. C. D.
9.如图,有一圆锥形粮堆,其侧面展开图是半径为6m的半圆,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程长为( )
A.3m B.m C.m D.4m
10.如图,AB是半圆O的直径,小宇按以下步骤作图:
(1)分别以A、B为圆心,大于AO长为半径作弧,两弧交于P点,连接OP与半圆交于C点;
(2)分别以A、C为圆心,大于AC长为半径作弧,两弧交于Q点,连接OQ与半圆交于D点;
(3)连接AD、BD、BC,BD与OC交于E点.
根据以上作图过程及所作图形,下轮结论:①BD平分∠ABC;②BC∥OD;③CE=OE.所有正确结论的序号是( )
A.①② B.②③ C.①③ D.①②③
11.如图,I为的内心,有一直线通过I点且分别与AB、AC相交于D点、E点若,,则I点到BC的距离为何?( )
A. B. C.2 D.3
12.如图,在正方形ABCD中,以BC为直径作半圆O,以D为圆心,DA为半径作,与半圆O交于点P,我们称:点P为正方形ABCD的一个“奇妙点”,过奇妙点的多条线段与正方形ABCD无论是位置关系还是数量关系,都具有不少优美的性质值得探究.连接PA、PB、PC、PD,并延长PD交AB于点F.下列结论中:①FD=FB+BC;②∠APC=135°;③S△PBC=AP2;④tan∠BAP=;其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
二、填空题:本题共6个小题,每小题3分,共18分。
13.矩形ABCD中,边AB=6cm,AD=8cm,以A为圆心作⊙A,使B、C、D三点有两个点在⊙A内有一点在⊙A外,则⊙A的半径r的取值范围是____.
14.已知⊙O的半径OA=1,弦AB的长为.若在⊙O上找一点C,使AC=,则∠BAC=______°.
15.当点A(1,2),B(3,﹣3),C(5,n)三点可以确定一个圆,则n需要满足的条件为 __.
16.如图,已知圆O为的内切圆,切点分别为D、E、F,且,,,则圆O的半径为______.
17.如图,正方形内接于,,分别与相切于点和点,的延长线与的延长线交于点.已知,则图中阴影部分的面积为___________.
18.如图,的半径为2,圆心的坐标为,点是上的任意一点,,且、与轴分别交于、两点,若点、点关于原点对称,当线段最短时,点的坐标为______.
三、解答题(19题6分,其余每题8分,共46分)
19.如图所示,在平面直角坐标系中,⊙P经过原点,交x轴于点A(4,0),交y轴于点B(0,3),点C是劣弧OA的中点,连接BC.
(1)求⊙P的半径
(2)求弦BC的长
20.如图,四边形ABCD为⊙O的内接四边形,BD=BC,BA、CD延长线交于点E.
(1)求证:∠EAD=∠BAC;
(2)若的度数为64°,则∠E的度数为 °.
21.如图,的半径OC垂直于弦AB,垂足为D.
(1)若,,求;
(2)若,,求AB的长.
(3)若BC平分,判断直线BE与的位置关系,并加以证明.
22.如图1,扇形的半径为4,圆心角为,点为上任意一点(不与点,重合),且于点,点为的内心,连接,,.
(1)求的度数;
(2)如图2,⊙为的外接圆,点在上运动.
①当时,判断与⊙的位置关系,并加以证明;
②设⊙的半径为,若的值不随点的运动而改变,请直接写出的值;若随着点的运动而在一个范围内变化,请直接写出这个变化范围.
23.如图,有一个直径MN=4的半圆形纸片,其圆心为点P,从初始阶段Ⅰ位置开始,在无滑动的情况下沿数轴向右翻滚至位置Ⅴ,其中位置Ⅰ中的MN平行于数轴,且半⊙P与数轴相切于原点O;位置Ⅱ和位置Ⅳ中MN的垂直于数轴;位置Ⅲ中的MN在数轴上;位置Ⅴ中的点N到数轴的距离为3,且半⊙P与数轴相切于点A.解答下列问题:
(1)位置Ⅰ中MN的与数轴之间的距离为 ;位置Ⅱ中的半⊙P与数轴位置关系是 ;
(2)求位置Ⅲ中的圆心P在数轴上表示的数;
(3)纸片半⊙P从位置Ⅲ翻滚到位置Ⅳ时,求点N所经过路径长及该纸片所扫过的图形的面积;
(4)求OA的长,(结果保留)
24.如图,在中,,,,动点从点出发,沿着方向以1个单位长度/秒的速度匀速运动,同时动点从点方向出发,沿着方向也以1个单位长度/秒的速度匀速运动,设运动时间为秒,以为圆心,长为半径的与、的另一个交点分别为、,连接、.
(1)当点与点重合时,求的值;
(2)若是等腰三角形,求的值;
(3)若与线段只有一个公共点,求的取值范围.
答案
一、选择题。
B.D.C.A.A.B.C.B.C.D.A.A.
二、填空题。
13.8cm
15.n≠﹣8.
16.2
17.5-π.
18..
三、解答题
19.
(1)解:∵⊙P过原点O,与x轴交于A(4,0),与y轴交于B(0,3),
∴AB是⊙O的直径,AO=4,BO=3,
由题意可得出:OA2+OB2=AB2,
∴AB=5,
∴⊙P的半径为;
(2)连接PC交OA于点H,连接AC,
∵点C是劣弧OA的中点,
∴OH=AH==2,PH⊥OA,
∵PA=,
∴PH==,
∴CH=PC-PH=-=1,
∴AC=,
∵AB为⊙P的直径,
∴∠ACB=90°,
∴BC==2.
20.
(1)证明:∵四边形ABCD为⊙O的内接四边形,
∴∠BAD+∠BCD=180°,
∵∠BAD+∠EAD=180°,
∴∠EAD=∠BCD,
∵BD=BC,
∴∠BDC=∠BCD,
由圆周角定理得:∠BAC=∠BDC=∠BCD,
∴∠EAD=∠BAC;
(2)解:∵的度数为64°,
∴∠ACB=32°,
∵四边形ABCD为⊙O的内接四边形,
∴∠EDA=∠ABC,
∵∠EAD=∠BAC,
∴∠E=180°-∠EAD-∠EDA=180°-∠BAC-∠ABC=∠ACB,
∴∠E=∠ACB=32°,
故答案为:32.
21.
(1)∵半径OC垂直于弦AB,
∴,
在中,,,
∴根据勾股定理,得,
∴,
在中,,,
∴;
(2)∵,
,
∵,
∴,
在中,,
∵半径OC垂直于弦AB,
∴;
(3)BE与相切.
证明如下:
如图所示,连接,∵平分,
∴,
∵,
∴,
∵,
∴,
∵半径垂直于弦,
∴,
∴,
∴.
∵是的半径,
∴为的切线.
22.
解:(1)∵点为的内心,
∴.
又∵,,
∴.
∵于点,
∴.
∴.
∴.
∴.
(2)①当时,与相切.
证明如下:
如图,在优弧上取一点,连接,.
∵点在劣弧上,且,
∴.
∴.
连接,.
∴.
∴.
而当时,
,
∴.
∴当时,与相切.
②的值是定值;.理由如下:
当点C在上运动时,由(2)证得,OM=MB=r,△OBM为等腰直角三角形,而OB=4,故OM=MB=.
23.
解:(1)位置Ⅰ中的MN平行于数轴,则与数轴的距离为半径2,
位置Ⅱ和位置Ⅳ中MN的垂直于数轴,
可判断位置Ⅱ中的半⊙P与数轴位置关系相切,
故答案为:2,相切;
(2)从位置Ⅰ到位置Ⅱ,的长等于数轴上的长,从位置Ⅱ到位置Ⅲ,数轴上的,故数轴上的,
,
位置Ⅲ中的圆心P在数轴上表示的数为;
(3)点N所经过路径长为,
S半圆=,S扇形=,
半⊙P所扫过图形的面积为2π+4π=6π;
(4)如图,作NC垂直数轴于点C,作PH⊥NC于点H,连接PA,
则四边形PHCA为矩形,
在Rt△NPH中,PN=2,NH=NC-HC=NC-PA=1,
于是sin∠NPH=,
∴∠NPH=30°,
∴∠MPA=60°,
从而的长为,
于是OA的长为.
24.
解:(1)∵OA=6,OB=8,
∴由勾股定理可求得:AB=10,
由题意知:OQ=AP=t,
∴AC=2t,
∵AC是⊙P的直径,
∴∠CDA=90°,
∴CD∥OB,
∴△ACD∽△ABO,
∴,
∴AD=,
当Q与D重合时,
AD+OQ=OA,
∴+t=6,
∴t=;
(2)若△ACQ是等腰三角形时,分三种情况讨论:
①当AQ=AC时,即AC=AQ=2t,OQ=t,
∵OQ+QA=6,
∴t+2t=6,
解得t=2;
②当QC=CA时,即QC=CA=2t,由(1)知DA=,
∴QD=DA=,
∴OQ+QD+DA=6,
∴,
解得:;
③当QC=QA时,如图,连接PQ,
可知PQ⊥AC,
∴∠QPA=∠BOA=90°,∠QAP=∠BAO,
∴△AQE∽△ABO,
则AE=t,AQ=6-t,
∴,
∴,
解得:;
综上所述,当△ACQ是等腰三角形时,t=2或或;
(3)当QC与⊙P相切时,如图
此时∠QCA=90°,
∵OQ=AP=t,
∴AQ=6﹣t,AC=2t,
∵∠A=∠A,
∠QCA=∠ABO,
∴△AQC∽△ABO,
∴,
∴,
∴t=,
∴当0<t≤时,⊙P与QC只有一个交点,
当QC⊥OA时,
此时Q与D重合,
由(1)可知:t=,
∴当<t≤5时,⊙P与QC只有一个交点,
综上所述,当,⊙P与QC只有一个交点,t的取值范围为:0<t≤或<t≤5.
