北师大版九年级数学下册试题 第三章 圆 复习卷(含答案)
文档属性
| 名称 | 北师大版九年级数学下册试题 第三章 圆 复习卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 605.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 09:45:20 | ||
图片预览



文档简介
第三章 《圆》复习卷
一、选择题。
1.设P为外一点,若点P到的最短距离为3,最长距离为7,则的半径为( )
A.2 B.4 C.4或10 D.2或5
2.如图,⊙O中,弦AB⊥CD,垂足为E,F为的中点,连接AF、BF、AC,AF交CD于M,过F作FH⊥AC,垂足为G,以下结论:①;②HC=BF:③MF=FC:④,其中成立的个数是( )
A.1个 B.2个 C.3个 D.4个
3.如图,已知⊙O的直径AD=10.任一圆周角∠ACB=45°,则弦AB的长为( )
A.5 B.5 C.5 D.5
4.如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA, 垂足为D.且DC+DA=12, ⊙O的直径为20,则AB的长等于( )
A.8 B.12 C.16 D.18
5.如图,⊙O为Rt△ABC的内切圆,∠C=90°,延长AO交BC于D点,若AC=4,CD=1,则BD的长为( )
A. B.1 C. D.
6.如图,边长为的正方形的中心与半径为的的圆心重合,,分别是,的延长线与的交点,则图中阴影部分的面积为( )
A. B. C. D.
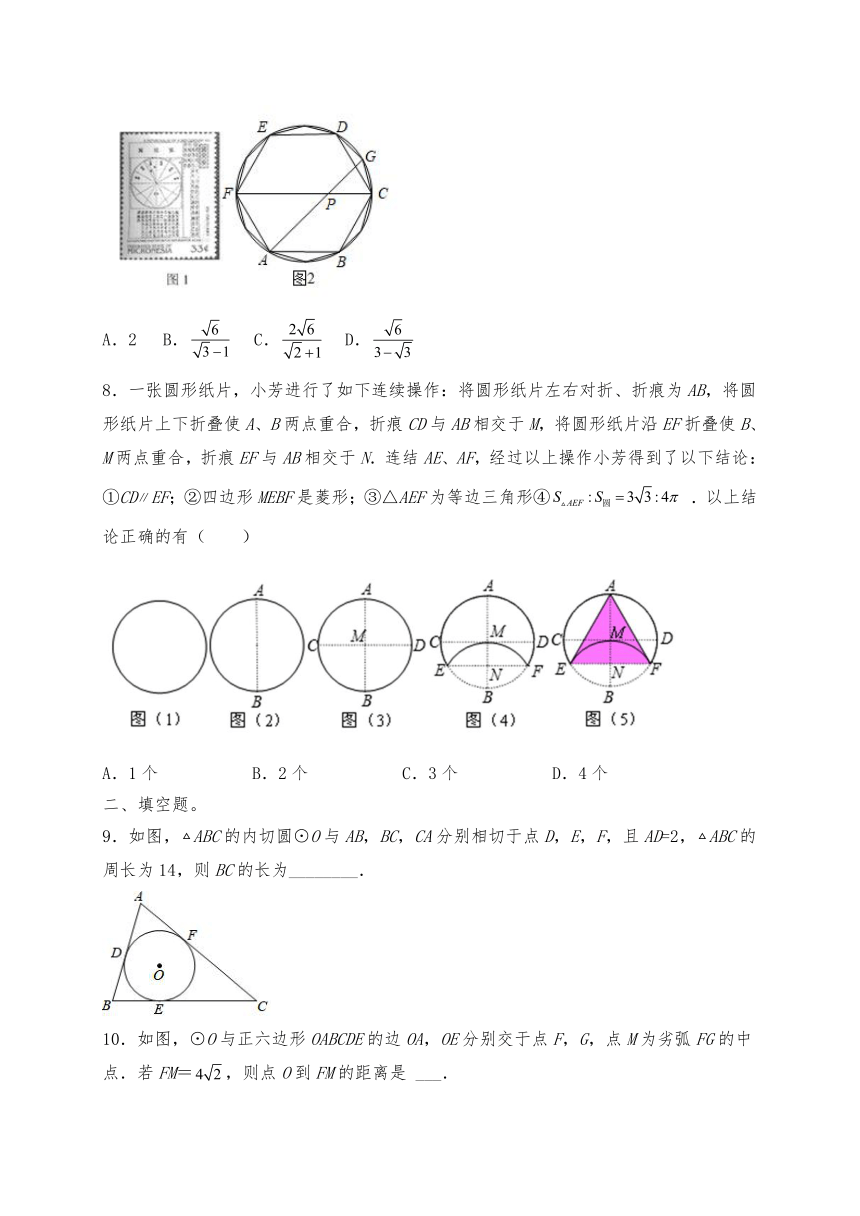
7.我国伟大的数学家刘徽于公元263年攥《九章算术注》中指出,“周三径一”不是圆周率值,实际上是圆内接正六边形周长和直径的比值(图1).刘徽发现,圆内接正多边形边数无限增加时,多边形的周长就无限逼近圆周长,从而创立“割圆术”,为计算圆周率建立起相当严密的理论和完善的算法.如图2,六边形是圆内接正六边形,把每段弧二等分,作出一个圆内接正十二边形,连结,,交于点P,,则( )
A.2 B. C. D.
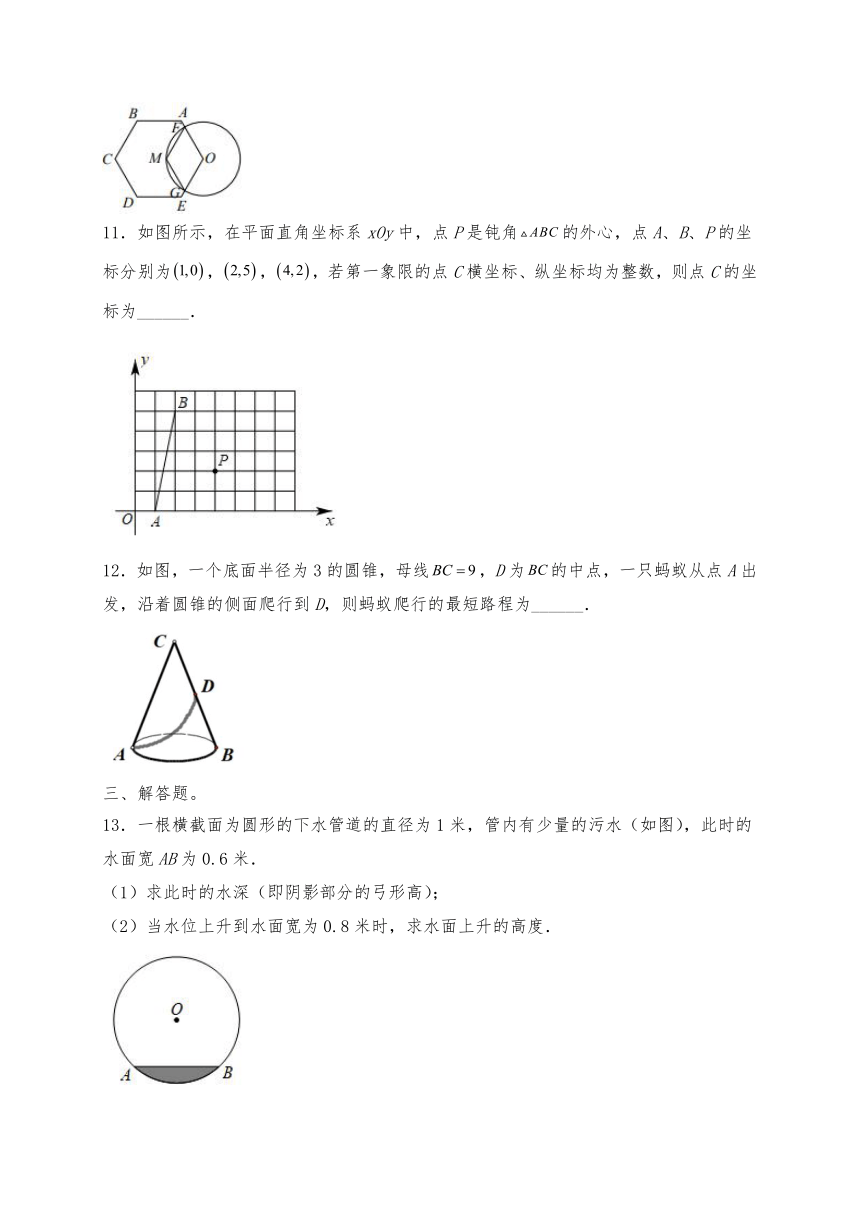
8.一张圆形纸片,小芳进行了如下连续操作:将圆形纸片左右对折、折痕为AB,将圆形纸片上下折叠使A、B两点重合,折痕CD与AB相交于M,将圆形纸片沿EF折叠使B、M两点重合,折痕EF与AB相交于N.连结AE、AF,经过以上操作小芳得到了以下结论:①CDEF;②四边形MEBF是菱形;③△AEF为等边三角形④ .以上结论正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题。
9.如图,ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,ABC的周长为14,则BC的长为________.
10.如图,⊙O与正六边形OABCDE的边OA,OE分别交于点F,G,点M为劣弧FG的中点.若FM=,则点O到FM的距离是 ___.
11.如图所示,在平面直角坐标系xOy中,点P是钝角的外心,点A、B、P的坐标分别为,,,若第一象限的点C横坐标、纵坐标均为整数,则点C的坐标为______.
12.如图,一个底面半径为3的圆锥,母线,D为的中点,一只蚂蚁从点A出发,沿着圆锥的侧面爬行到D,则蚂蚁爬行的最短路程为______.
三、解答题。
13.一根横截面为圆形的下水管道的直径为1米,管内有少量的污水(如图),此时的水面宽AB为0.6米.
(1)求此时的水深(即阴影部分的弓形高);
(2)当水位上升到水面宽为0.8米时,求水面上升的高度.
14.如图,正方形ABCD的边长为4cm,点E、F分别从点D和点C出发,沿着射线DA、射线CD运动,且DE=CF,直线AF、直线BE交于H点.
(1)当点E从点D向点A运动的过程中:
①求证:AF⊥BE;
②在图中画出点H运动路径并求出点H运动的路径长;
(2)在整个运动过程中:
①线段DH长度的最小值为______.
②线段DH长度的最大值为_________ .
15.如图,AB是⊙O的直径,点C是⊙O上一点,点C是⊙O上一点,AD⊥CD于点D,且AC平分∠DAB,延长CD交AB的延长线于点P,弦CE平分∠ACB,交AB于点F,过点C作直线CP与AB的延长线相交于点P,且PC=PF,连接BE.
(1)求证:△BCE∽△FBE;
(2)求证:PC为⊙O的切线;
(3)若tan∠ABC=2,BE=2,求线段PC的长.
答案
一、选择题。
A.C.B.B.C.A.D.D.
二、填空题。
9.5.
10..
11.(1,4)或(6,5)
12.
三、解答题。
13.
解:(1)作半径,垂足为点,连接,则即为弓形的高,
∵,
∴,
∵,,
∴,
∴,
∴米,即此时的水深为0.1米.
(2)当水位上升到水面宽为0.8米时,直线与相交于点
同理可得,当与在圆心同侧时,水面上升的高度为0.1米;当在在圆心异侧时水面上升的高度为0.7米.
∴综上所述,当水位上升到水面宽为0.8米时,水面上升的高度为0.1米或0.7米.
14.
(1)①∵四边形ABCD是正方形,
∴AB=DA=CD,∠BAE=∠ADF=90°,
∵DE=CF,
∴AE=DF,
∴△ABE≌△DAF,
∴∠ABE=∠DAF,
∵∠ABE+∠AEB=90°,
∴∠DAF+∠AEB=90°,
∴∠AHE=90°,
∴AF⊥BE;
②点H运动路径画图如下,
∵∠AHB=90°,且AB是定长,
∴点H在以AB为直径的圆上,且H可以与M,B重合即运动路径是一段优弧,
设AB的中点为点O,连接BD,设BD 的中点为点M,连接OM
∴∠BOM=90°,
∵AB=4,
∴圆的半径为2,
∴弧长为=3π;
(2)①根据圆的性质,当O,H,D共线,且H在O,D之间时最短,当H与点G重合时,最短,
∵AD=4,AO=2,
∴DO==;
∴DH=DO-OG=,
故答案为:.
②根据圆的性质,当O,H,D共线,且H在O,D之外时最大,当H与点Q重合时,最大,
∵AD=4,AO=2,
∴DO==;
∴DH=DO+OQ=,
故答案为:.
15.
(1)证明:AB是⊙O的直径,
∴∠ACB=90°,
∵CE平分∠ACB,
∴∠ACE=∠BCE=45°,
∵∠ACE=∠ABE,
∴∠BCE=∠ABE即∠BCE=∠FBE,
∵∠CEB=∠BCF,
∴△BCE∽△BCF;
(2)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵OA=OC,
∴∠ACO=∠CAO,
∴∠DAC=∠ACO,
∴CO∥AD,
∵AD⊥CD,
∴OC⊥CD,
∴PC为⊙O的切线;
(3)连结AE,过B作BG⊥CE于G,
∵∠ACE=∠BCE,
∴
∴AE=CE=2
∵AB为直径,
∴∠AEB=90°,
∴AB=,
∵tan∠ABC=2
∴
∴AC=2BC,
∵AC2+BC2=AB2,
∴,
解得,AC=8,
∵BG⊥CE,∠GCB=45°,
∴∠CBG=90°-∠GCB=45°=∠GCB,
∴CG=BG=sin45°CB=,
在Rt△GBE中,GE=,
∴CE=CG+GE=,
由(1)知△BCE∽△BCF;
∴,即,
解得,
∵∠OCP=∠ACB=90°,
∴∠ACO+∠OCB=∠OCB+∠BCP,
∴∠ACO=∠BCP,
∵∠CAO=∠ACO,
∴∠CAO=∠BCP,即∠CAP=∠BCP,
∴∠APC=∠CPB,
∴△APC∽△CPB,
∴,
∵PC=PF,
∴PB=PF-BF=PC-BF=PC-,PA=PB+AB=PC-+=PC+,
∴,
整理得,
解得.
经检验满足方程并符合题意,
∴线段PC的长为.
一、选择题。
1.设P为外一点,若点P到的最短距离为3,最长距离为7,则的半径为( )
A.2 B.4 C.4或10 D.2或5
2.如图,⊙O中,弦AB⊥CD,垂足为E,F为的中点,连接AF、BF、AC,AF交CD于M,过F作FH⊥AC,垂足为G,以下结论:①;②HC=BF:③MF=FC:④,其中成立的个数是( )
A.1个 B.2个 C.3个 D.4个
3.如图,已知⊙O的直径AD=10.任一圆周角∠ACB=45°,则弦AB的长为( )
A.5 B.5 C.5 D.5
4.如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA, 垂足为D.且DC+DA=12, ⊙O的直径为20,则AB的长等于( )
A.8 B.12 C.16 D.18
5.如图,⊙O为Rt△ABC的内切圆,∠C=90°,延长AO交BC于D点,若AC=4,CD=1,则BD的长为( )
A. B.1 C. D.
6.如图,边长为的正方形的中心与半径为的的圆心重合,,分别是,的延长线与的交点,则图中阴影部分的面积为( )
A. B. C. D.
7.我国伟大的数学家刘徽于公元263年攥《九章算术注》中指出,“周三径一”不是圆周率值,实际上是圆内接正六边形周长和直径的比值(图1).刘徽发现,圆内接正多边形边数无限增加时,多边形的周长就无限逼近圆周长,从而创立“割圆术”,为计算圆周率建立起相当严密的理论和完善的算法.如图2,六边形是圆内接正六边形,把每段弧二等分,作出一个圆内接正十二边形,连结,,交于点P,,则( )
A.2 B. C. D.
8.一张圆形纸片,小芳进行了如下连续操作:将圆形纸片左右对折、折痕为AB,将圆形纸片上下折叠使A、B两点重合,折痕CD与AB相交于M,将圆形纸片沿EF折叠使B、M两点重合,折痕EF与AB相交于N.连结AE、AF,经过以上操作小芳得到了以下结论:①CDEF;②四边形MEBF是菱形;③△AEF为等边三角形④ .以上结论正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题。
9.如图,ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,ABC的周长为14,则BC的长为________.
10.如图,⊙O与正六边形OABCDE的边OA,OE分别交于点F,G,点M为劣弧FG的中点.若FM=,则点O到FM的距离是 ___.
11.如图所示,在平面直角坐标系xOy中,点P是钝角的外心,点A、B、P的坐标分别为,,,若第一象限的点C横坐标、纵坐标均为整数,则点C的坐标为______.
12.如图,一个底面半径为3的圆锥,母线,D为的中点,一只蚂蚁从点A出发,沿着圆锥的侧面爬行到D,则蚂蚁爬行的最短路程为______.
三、解答题。
13.一根横截面为圆形的下水管道的直径为1米,管内有少量的污水(如图),此时的水面宽AB为0.6米.
(1)求此时的水深(即阴影部分的弓形高);
(2)当水位上升到水面宽为0.8米时,求水面上升的高度.
14.如图,正方形ABCD的边长为4cm,点E、F分别从点D和点C出发,沿着射线DA、射线CD运动,且DE=CF,直线AF、直线BE交于H点.
(1)当点E从点D向点A运动的过程中:
①求证:AF⊥BE;
②在图中画出点H运动路径并求出点H运动的路径长;
(2)在整个运动过程中:
①线段DH长度的最小值为______.
②线段DH长度的最大值为_________ .
15.如图,AB是⊙O的直径,点C是⊙O上一点,点C是⊙O上一点,AD⊥CD于点D,且AC平分∠DAB,延长CD交AB的延长线于点P,弦CE平分∠ACB,交AB于点F,过点C作直线CP与AB的延长线相交于点P,且PC=PF,连接BE.
(1)求证:△BCE∽△FBE;
(2)求证:PC为⊙O的切线;
(3)若tan∠ABC=2,BE=2,求线段PC的长.
答案
一、选择题。
A.C.B.B.C.A.D.D.
二、填空题。
9.5.
10..
11.(1,4)或(6,5)
12.
三、解答题。
13.
解:(1)作半径,垂足为点,连接,则即为弓形的高,
∵,
∴,
∵,,
∴,
∴,
∴米,即此时的水深为0.1米.
(2)当水位上升到水面宽为0.8米时,直线与相交于点
同理可得,当与在圆心同侧时,水面上升的高度为0.1米;当在在圆心异侧时水面上升的高度为0.7米.
∴综上所述,当水位上升到水面宽为0.8米时,水面上升的高度为0.1米或0.7米.
14.
(1)①∵四边形ABCD是正方形,
∴AB=DA=CD,∠BAE=∠ADF=90°,
∵DE=CF,
∴AE=DF,
∴△ABE≌△DAF,
∴∠ABE=∠DAF,
∵∠ABE+∠AEB=90°,
∴∠DAF+∠AEB=90°,
∴∠AHE=90°,
∴AF⊥BE;
②点H运动路径画图如下,
∵∠AHB=90°,且AB是定长,
∴点H在以AB为直径的圆上,且H可以与M,B重合即运动路径是一段优弧,
设AB的中点为点O,连接BD,设BD 的中点为点M,连接OM
∴∠BOM=90°,
∵AB=4,
∴圆的半径为2,
∴弧长为=3π;
(2)①根据圆的性质,当O,H,D共线,且H在O,D之间时最短,当H与点G重合时,最短,
∵AD=4,AO=2,
∴DO==;
∴DH=DO-OG=,
故答案为:.
②根据圆的性质,当O,H,D共线,且H在O,D之外时最大,当H与点Q重合时,最大,
∵AD=4,AO=2,
∴DO==;
∴DH=DO+OQ=,
故答案为:.
15.
(1)证明:AB是⊙O的直径,
∴∠ACB=90°,
∵CE平分∠ACB,
∴∠ACE=∠BCE=45°,
∵∠ACE=∠ABE,
∴∠BCE=∠ABE即∠BCE=∠FBE,
∵∠CEB=∠BCF,
∴△BCE∽△BCF;
(2)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵OA=OC,
∴∠ACO=∠CAO,
∴∠DAC=∠ACO,
∴CO∥AD,
∵AD⊥CD,
∴OC⊥CD,
∴PC为⊙O的切线;
(3)连结AE,过B作BG⊥CE于G,
∵∠ACE=∠BCE,
∴
∴AE=CE=2
∵AB为直径,
∴∠AEB=90°,
∴AB=,
∵tan∠ABC=2
∴
∴AC=2BC,
∵AC2+BC2=AB2,
∴,
解得,AC=8,
∵BG⊥CE,∠GCB=45°,
∴∠CBG=90°-∠GCB=45°=∠GCB,
∴CG=BG=sin45°CB=,
在Rt△GBE中,GE=,
∴CE=CG+GE=,
由(1)知△BCE∽△BCF;
∴,即,
解得,
∵∠OCP=∠ACB=90°,
∴∠ACO+∠OCB=∠OCB+∠BCP,
∴∠ACO=∠BCP,
∵∠CAO=∠ACO,
∴∠CAO=∠BCP,即∠CAP=∠BCP,
∴∠APC=∠CPB,
∴△APC∽△CPB,
∴,
∵PC=PF,
∴PB=PF-BF=PC-BF=PC-,PA=PB+AB=PC-+=PC+,
∴,
整理得,
解得.
经检验满足方程并符合题意,
∴线段PC的长为.
