14.1.1 直角三角形三边的关系 课件(共15张PPT)
文档属性
| 名称 | 14.1.1 直角三角形三边的关系 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 21:50:08 | ||
图片预览




文档简介
(共15张PPT)
14.1.1 直角三角形三边的关系
教学目标
知识技能:
了解勾股定理的文化背景,体验勾股定理的探索过程.
数学思考:
在勾股定理的探索过程中,发展合情推理能力,体会数形结合的思想.
解决问题:
1.通过拼图活动,体验数学思维的严谨性,发展形象思维.
2.在探究活动中,学会与人合作并能与他人交流思维的过程和探究结果.
情感态度:
1.通过对勾股定理历史的了解,感受数学文化,激发学习热情.
2.在探究活动中,体验解决问题方法的多样性,培养学生的合作交流意识和探索精神.
教学重难点
重点:探索和证明勾股定理
难点:用拼图方法证明勾股定理
一、情境引入
在2002年的国际数学家大会上采用弦图
作为会徽,它为什么有如此大的魅力呢?它蕴涵着怎样迷人的奥妙呢?
R
Q
P
C
A
B
图14.1.1
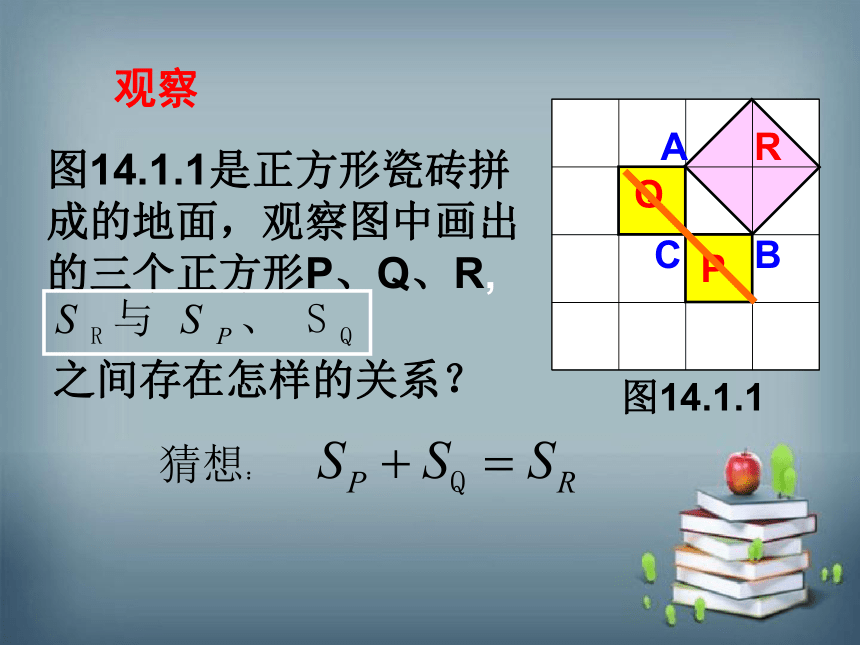
图14.1.1是正方形瓷砖拼成的地面,观察图中画出的三个正方形P、Q、R,
之间存在怎样的关系?
观察
猜想:
c
b
a
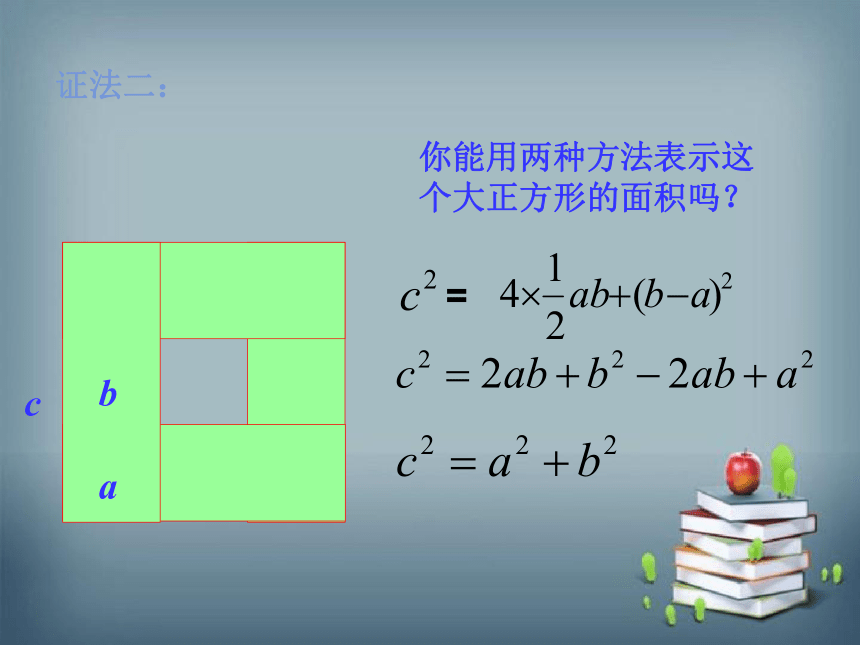
你能用两种方法表示这个大正方形的面积吗?
=
证法二:
a
b
c
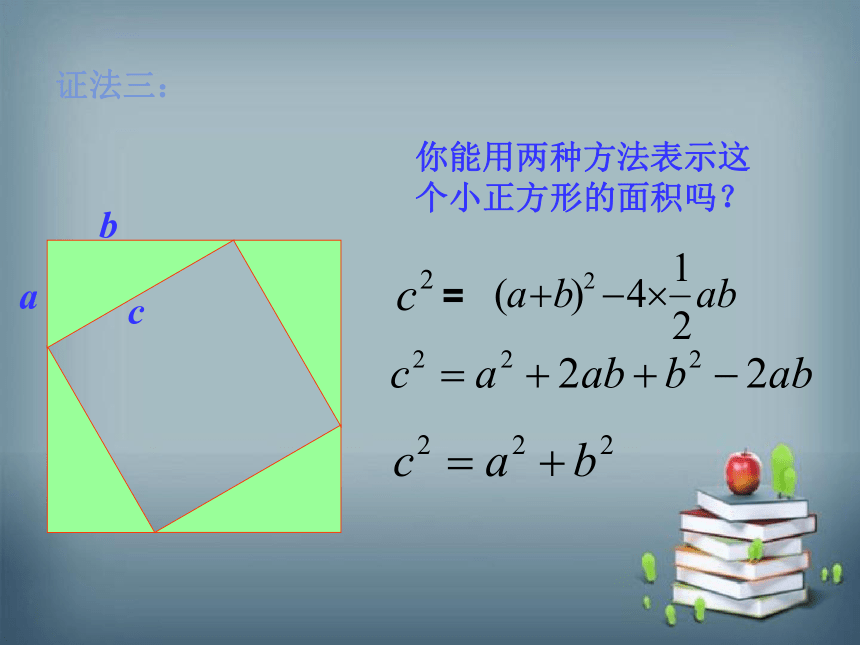
你能用两种方法表示这个小正方形的面积吗?
=
证法三:
等腰直角三角形是特殊的直角三角形,一般的直角三角形是否也具有“两直角边的平方和等于斜边的平方”呢?观察图14.1.2,如果每一小方格的面积代表单位1,那么可以得到什么结论?
勾股定理
对于任意直角三角形,如果两直角边分别为a、b,斜边为c,那么一定有
即 直角三角形两直角边的平方和等于斜边的平方.
a
b
c
如果知道了直角三角形两边的长度,那么应用勾股定理可以求出第三边的长度
勾股定理的由来:在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”。所以我国古代把上面的定理称为“勾股定理”。
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。
c
b
a
c2=a2 + b2
a2=c2-b2
b2 =c2-a2
例1 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.
例题分析
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
方法小结
随堂练习
1、 在△ABC中,∠C=90°(1)若a=6,b=10,则c= ; (2)若a=24,c=25,b= 。
2、若直角三角形中,有两边长是3和4,则第三边长的平方为( )
A 25 B 14 C 7 D 7或25
3、求下列图中未知数X,Y的值
2、隔湖有两点A、B,从与BA方向成直角 的BC方向上的点C测得CA=13米,CB=12米,则AB为 ( )
A
B
C
A.5米 B.12米 C.10米 D.13米
13
12
A
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
a
b
c
课堂小结
1、你在本堂课中主要收获了什么?
2、该定理解释了哪一类三角形中的什么元素之间的关系?
3、在探索和验证定理的过程中,我们运用了哪些方法?
14.1.1 直角三角形三边的关系
教学目标
知识技能:
了解勾股定理的文化背景,体验勾股定理的探索过程.
数学思考:
在勾股定理的探索过程中,发展合情推理能力,体会数形结合的思想.
解决问题:
1.通过拼图活动,体验数学思维的严谨性,发展形象思维.
2.在探究活动中,学会与人合作并能与他人交流思维的过程和探究结果.
情感态度:
1.通过对勾股定理历史的了解,感受数学文化,激发学习热情.
2.在探究活动中,体验解决问题方法的多样性,培养学生的合作交流意识和探索精神.
教学重难点
重点:探索和证明勾股定理
难点:用拼图方法证明勾股定理
一、情境引入
在2002年的国际数学家大会上采用弦图
作为会徽,它为什么有如此大的魅力呢?它蕴涵着怎样迷人的奥妙呢?
R
Q
P
C
A
B
图14.1.1
图14.1.1是正方形瓷砖拼成的地面,观察图中画出的三个正方形P、Q、R,
之间存在怎样的关系?
观察
猜想:
c
b
a
你能用两种方法表示这个大正方形的面积吗?
=
证法二:
a
b
c
你能用两种方法表示这个小正方形的面积吗?
=
证法三:
等腰直角三角形是特殊的直角三角形,一般的直角三角形是否也具有“两直角边的平方和等于斜边的平方”呢?观察图14.1.2,如果每一小方格的面积代表单位1,那么可以得到什么结论?
勾股定理
对于任意直角三角形,如果两直角边分别为a、b,斜边为c,那么一定有
即 直角三角形两直角边的平方和等于斜边的平方.
a
b
c
如果知道了直角三角形两边的长度,那么应用勾股定理可以求出第三边的长度
勾股定理的由来:在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”。所以我国古代把上面的定理称为“勾股定理”。
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方。
c
b
a
c2=a2 + b2
a2=c2-b2
b2 =c2-a2
例1 .在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.
例题分析
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
方法小结
随堂练习
1、 在△ABC中,∠C=90°(1)若a=6,b=10,则c= ; (2)若a=24,c=25,b= 。
2、若直角三角形中,有两边长是3和4,则第三边长的平方为( )
A 25 B 14 C 7 D 7或25
3、求下列图中未知数X,Y的值
2、隔湖有两点A、B,从与BA方向成直角 的BC方向上的点C测得CA=13米,CB=12米,则AB为 ( )
A
B
C
A.5米 B.12米 C.10米 D.13米
13
12
A
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
a
b
c
课堂小结
1、你在本堂课中主要收获了什么?
2、该定理解释了哪一类三角形中的什么元素之间的关系?
3、在探索和验证定理的过程中,我们运用了哪些方法?
