14.1.1 直角三角形三边的关系 同步练习(含答案)
文档属性
| 名称 | 14.1.1 直角三角形三边的关系 同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 439.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 00:00:00 | ||
图片预览


文档简介
14.1.1 直角三角形三边的关系
一、单选题
1.如图,在△ABC中,∠ABC=90°,AB=3,BC=1,AB在数轴上,以点A为圆心,AC长为半径作弧,交数轴的正半轴于点M,则M表示的数为( )
A.2.1 B.-1 C. D.+1
2.在勾股定理的学习过程中,我们已经学会了运用以下图形,验证著名的勾股定理:这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数,图形与几何等领域中的许多数学公式和规律,它体现的数学思想是( )
A.统计思想 B.分类思想 C.数形结合思想 D.函数思想
3.如图,点A表示的实数是( )
A.﹣ B.﹣ C.﹣ D.﹣
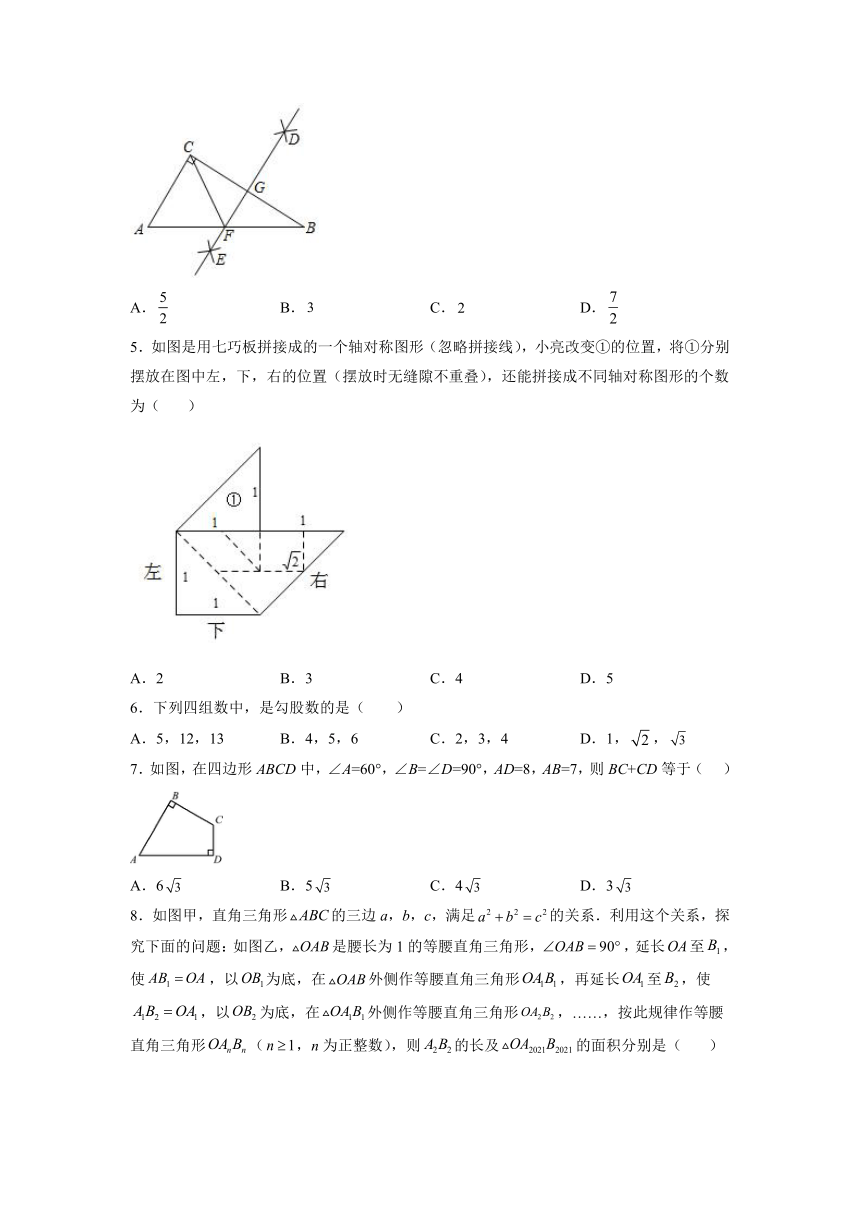
4.如图,在中,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于两点,作直线交于点,交于点,连结.若,则的长为( )
A. B. C. D.
5.如图是用七巧板拼接成的一个轴对称图形(忽略拼接线),小亮改变①的位置,将①分别摆放在图中左,下,右的位置(摆放时无缝隙不重叠),还能拼接成不同轴对称图形的个数为( )
A.2 B.3 C.4 D.5
6.下列四组数中,是勾股数的是( )
A.5,12,13 B.4,5,6 C.2,3,4 D.1,,
7.如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,AD=8,AB=7,则BC+CD等于( )
A.6 B.5 C.4 D.3
8.如图甲,直角三角形的三边a,b,c,满足的关系.利用这个关系,探究下面的问题:如图乙,是腰长为1的等腰直角三角形,,延长至,使,以为底,在外侧作等腰直角三角形,再延长至,使,以为底,在外侧作等腰直角三角形,……,按此规律作等腰直角三角形(,n为正整数),则的长及的面积分别是( )
A.2, B.4, C., D.2,
9.《九章算术》提供了许多整勾股数,如(3,4,5),(5,12,13),(7,24,25)等,并把一组勾股数中最大的数称为“弦数”.后人在此基础上进一步研究,得到如下规律:若m是大于1的奇数,把它平方后拆成相邻的两个整数,那么m与这两个整数构成组勾股数;若m是大于2的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1得到两个整数,那么m与这两个整数构成组勾股数.由上述方法得到的勾股数称为“由m生成的勾股数”.根据以上规律,“由8生成的勾股数”的“弦数”为( )
A.16 B.17 C.25 D.64
10.如图,点P是以A为圆心,AB为半径的圆弧与数轴的交点,则数轴上点P表示的实数是( )
A.-2 B.-2.2 C.- D.-+1
11.如图,在△ABC中,AB=2,∠ABC=60°,∠ACB=45°,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为( )
A. B.2 C.2 D.3
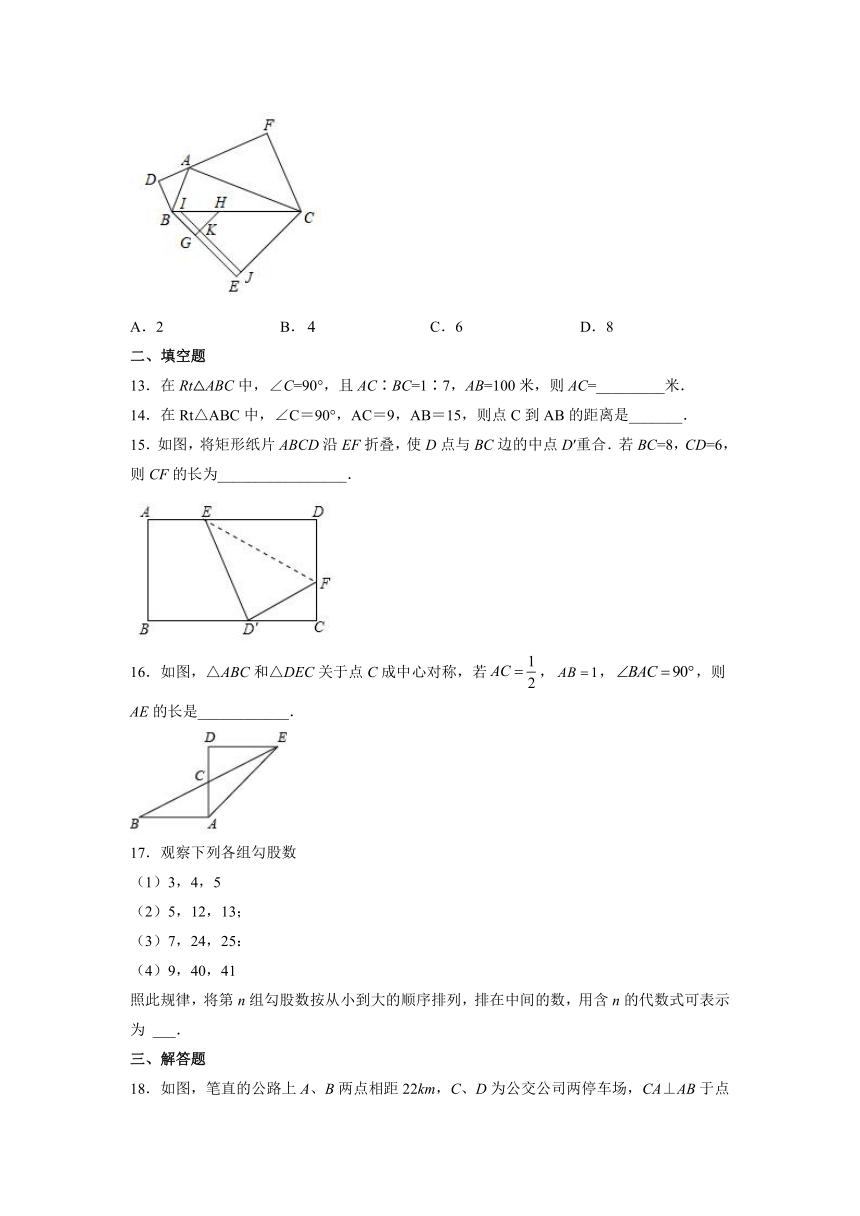
12.如图,在中,,以各边为斜边分别向外作等腰、等腰、等腰,将等腰和等腰按如图方式叠放到等腰中,已知,,则长为( )
A.2 B. C.6 D.8
二、填空题
13.在Rt△ABC中,∠C=90°,且AC∶BC=1∶7,AB=100米,则AC=_________米.
14.在Rt△ABC中,∠C=90°,AC=9,AB=15,则点C到AB的距离是_______.
15.如图,将矩形纸片ABCD沿EF折叠,使D点与BC边的中点D′重合.若BC=8,CD=6,则CF的长为_________________.
16.如图,△ABC和△DEC关于点C成中心对称,若,,,则AE的长是____________.
17.观察下列各组勾股数
(1)3,4,5
(2)5,12,13;
(3)7,24,25:
(4)9,40,41
照此规律,将第n组勾股数按从小到大的顺序排列,排在中间的数,用含n的代数式可表示为 ___.
三、解答题
18.如图,笔直的公路上A、B两点相距22km,C、D为公交公司两停车场,CA⊥AB于点A,DB⊥AB于点B,已知CA=6km,DB=16km,现在要在公路的AB段上建一个加油站M,使得C、D公交公司两停车场到加油站M的距离CM=DM,则加油站M应建在离B点多远处?
19.如图和都是等腰直角三角形,,,顶点在的斜边上,求证:.
20.中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展,现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°.AC=b,BC=a,AB=c,请你利用这个图形解决下列问题:
(1)试说明:a2+b2=c2;
(2)如果大正方形的面积是13,小正方形的面积是3,求(a+b)2的值.
参考答案
1--10BCBAB ABABD 11--12AD
13.
14.
15.
16.
17.
18.解:∵使得C、D公交公司两停车场到加油站M的距离相等,
∴CM=DM,
∵CA⊥AB于点A,DB⊥AB于点B,
∴∠A =∠B=90°,
∴AC2+AM2=CM2,BM2+BD2=MD2,
∴AC2+AM2=BM2+BD2,
设BM=xkm,AM=(22-x)km,CA=6km,DB=16km,
∴,
解得,
加油站M应建在离B点6km远.
19.证明:如图,连结BD ,
∵,
∴.
∴在△EAC和△DBC中,,
∴.
∴ .
又∵,
∴ .
∴ 在中,,
∴.
∵ 在中,,
∴ .
20.解:(1)∵大正方形面积为c2,直角三角形面积为ab,小正方形面积为(b﹣a)2,
∴c2=4×ab+(a﹣b)2=2ab+a2﹣2ab+b2即c2=a2+b2;
(2)由图可知:
(b﹣a)2=3,4×ab=13﹣3=10,
∴2ab=10,
∴(a+b)2=(b﹣a)2+4ab=3+2×10=23.
一、单选题
1.如图,在△ABC中,∠ABC=90°,AB=3,BC=1,AB在数轴上,以点A为圆心,AC长为半径作弧,交数轴的正半轴于点M,则M表示的数为( )
A.2.1 B.-1 C. D.+1
2.在勾股定理的学习过程中,我们已经学会了运用以下图形,验证著名的勾股定理:这种根据图形直观推论或验证数学规律和公式的方法,简称为“无字证明”.实际上它也可用于验证数与代数,图形与几何等领域中的许多数学公式和规律,它体现的数学思想是( )
A.统计思想 B.分类思想 C.数形结合思想 D.函数思想
3.如图,点A表示的实数是( )
A.﹣ B.﹣ C.﹣ D.﹣
4.如图,在中,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于两点,作直线交于点,交于点,连结.若,则的长为( )
A. B. C. D.
5.如图是用七巧板拼接成的一个轴对称图形(忽略拼接线),小亮改变①的位置,将①分别摆放在图中左,下,右的位置(摆放时无缝隙不重叠),还能拼接成不同轴对称图形的个数为( )
A.2 B.3 C.4 D.5
6.下列四组数中,是勾股数的是( )
A.5,12,13 B.4,5,6 C.2,3,4 D.1,,
7.如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,AD=8,AB=7,则BC+CD等于( )
A.6 B.5 C.4 D.3
8.如图甲,直角三角形的三边a,b,c,满足的关系.利用这个关系,探究下面的问题:如图乙,是腰长为1的等腰直角三角形,,延长至,使,以为底,在外侧作等腰直角三角形,再延长至,使,以为底,在外侧作等腰直角三角形,……,按此规律作等腰直角三角形(,n为正整数),则的长及的面积分别是( )
A.2, B.4, C., D.2,
9.《九章算术》提供了许多整勾股数,如(3,4,5),(5,12,13),(7,24,25)等,并把一组勾股数中最大的数称为“弦数”.后人在此基础上进一步研究,得到如下规律:若m是大于1的奇数,把它平方后拆成相邻的两个整数,那么m与这两个整数构成组勾股数;若m是大于2的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1得到两个整数,那么m与这两个整数构成组勾股数.由上述方法得到的勾股数称为“由m生成的勾股数”.根据以上规律,“由8生成的勾股数”的“弦数”为( )
A.16 B.17 C.25 D.64
10.如图,点P是以A为圆心,AB为半径的圆弧与数轴的交点,则数轴上点P表示的实数是( )
A.-2 B.-2.2 C.- D.-+1
11.如图,在△ABC中,AB=2,∠ABC=60°,∠ACB=45°,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为( )
A. B.2 C.2 D.3
12.如图,在中,,以各边为斜边分别向外作等腰、等腰、等腰,将等腰和等腰按如图方式叠放到等腰中,已知,,则长为( )
A.2 B. C.6 D.8
二、填空题
13.在Rt△ABC中,∠C=90°,且AC∶BC=1∶7,AB=100米,则AC=_________米.
14.在Rt△ABC中,∠C=90°,AC=9,AB=15,则点C到AB的距离是_______.
15.如图,将矩形纸片ABCD沿EF折叠,使D点与BC边的中点D′重合.若BC=8,CD=6,则CF的长为_________________.
16.如图,△ABC和△DEC关于点C成中心对称,若,,,则AE的长是____________.
17.观察下列各组勾股数
(1)3,4,5
(2)5,12,13;
(3)7,24,25:
(4)9,40,41
照此规律,将第n组勾股数按从小到大的顺序排列,排在中间的数,用含n的代数式可表示为 ___.
三、解答题
18.如图,笔直的公路上A、B两点相距22km,C、D为公交公司两停车场,CA⊥AB于点A,DB⊥AB于点B,已知CA=6km,DB=16km,现在要在公路的AB段上建一个加油站M,使得C、D公交公司两停车场到加油站M的距离CM=DM,则加油站M应建在离B点多远处?
19.如图和都是等腰直角三角形,,,顶点在的斜边上,求证:.
20.中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展,现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°.AC=b,BC=a,AB=c,请你利用这个图形解决下列问题:
(1)试说明:a2+b2=c2;
(2)如果大正方形的面积是13,小正方形的面积是3,求(a+b)2的值.
参考答案
1--10BCBAB ABABD 11--12AD
13.
14.
15.
16.
17.
18.解:∵使得C、D公交公司两停车场到加油站M的距离相等,
∴CM=DM,
∵CA⊥AB于点A,DB⊥AB于点B,
∴∠A =∠B=90°,
∴AC2+AM2=CM2,BM2+BD2=MD2,
∴AC2+AM2=BM2+BD2,
设BM=xkm,AM=(22-x)km,CA=6km,DB=16km,
∴,
解得,
加油站M应建在离B点6km远.
19.证明:如图,连结BD ,
∵,
∴.
∴在△EAC和△DBC中,,
∴.
∴ .
又∵,
∴ .
∴ 在中,,
∴.
∵ 在中,,
∴ .
20.解:(1)∵大正方形面积为c2,直角三角形面积为ab,小正方形面积为(b﹣a)2,
∴c2=4×ab+(a﹣b)2=2ab+a2﹣2ab+b2即c2=a2+b2;
(2)由图可知:
(b﹣a)2=3,4×ab=13﹣3=10,
∴2ab=10,
∴(a+b)2=(b﹣a)2+4ab=3+2×10=23.
