14.1.3 反证法 课件(共12张PPT)
文档属性
| 名称 | 14.1.3 反证法 课件(共12张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 281.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 22:01:08 | ||
图片预览




文档简介
(共12张PPT)
14.1.3 反证法
教学目标
(1)1.通过实例,体会反证法的含义.
2.了解反证法的基本步骤,会用反证法证明简单的命题.
(2)通过利用反证法证明命题,体会逆向思维.
(3)在观察、操作、推理等探索过程中,体验数学活动充满探索性和创造性;渗透事物之间的相互对立、相互矛盾、相互转化的辩证唯物主义思想.
教学重难点
教学重点:运用反证法进行推理论证.
教学难点:理解“反证法”证明得出“矛盾的所在”.
一、问题情境
小华睡觉前,地上是干的,早晨起来,看见地上全湿了。小华对婷婷说:“昨天晚上下雨了。”
你能对小华的判断说出理由吗?
假设昨天晚上没有下雨,那么地上应是干的,这与早晨地上全湿了相矛盾,所以说昨晚下雨是正确的。
小华的理由:
我们可以把这种说理方法应用到数学问题上。
情景导入
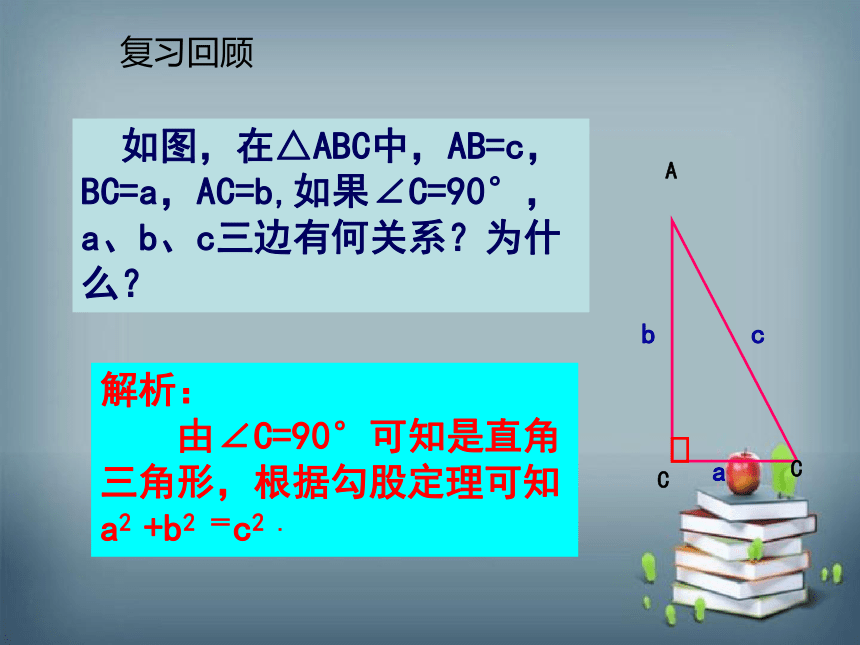
解析:
由∠C=90°可知是直角三角形,根据勾股定理可知
a2 +b2 =c2 .
如图,在△ABC中,AB=c,BC=a,AC=b,如果∠C=90°,a、b、c三边有何关系?为什么?
A
C
C
a
b
c
复习回顾
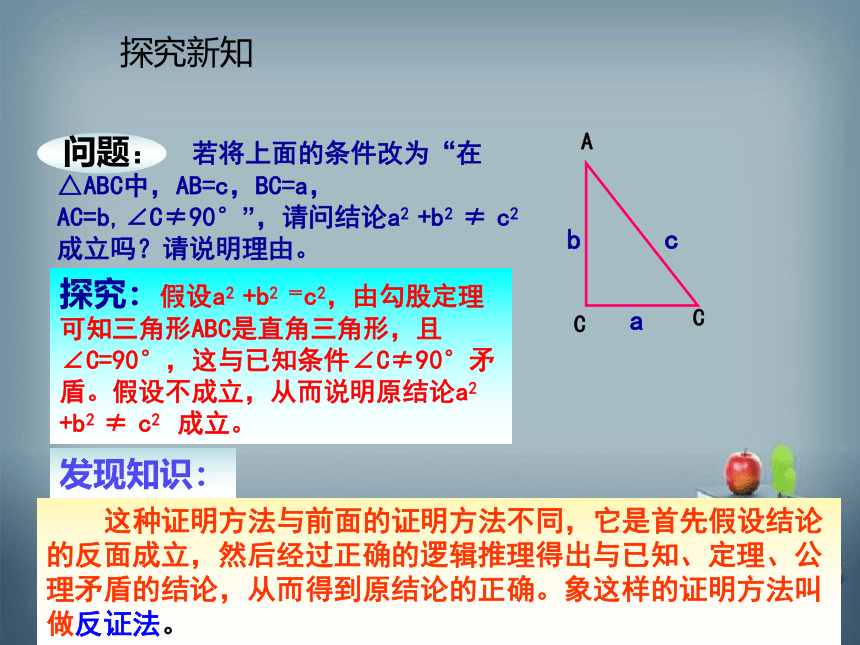
探究:假设a2 +b2 =c2,由勾股定理可知三角形ABC是直角三角形,且∠C=90°,这与已知条件∠C≠90°矛盾。假设不成立,从而说明原结论a2 +b2 ≠ c2 成立。
A
C
C
若将上面的条件改为“在△ABC中,AB=c,BC=a, AC=b,∠C≠90°”,请问结论a2 +b2 ≠ c2 成立吗?请说明理由。
a
b
c
这种证明方法与前面的证明方法不同,它是首先假设结论的反面成立,然后经过正确的逻辑推理得出与已知、定理、公理矛盾的结论,从而得到原结论的正确。象这样的证明方法叫做反证法。
问题:
发现知识:
探究新知
1、试说出下列命题的反面:
(1)a是实数。 (2)a大于2。
(3)a小于2。 (4)至少有2个
(5)最多有一个 (6)两条直线平行。
2、用反证法证明“若a2≠ b2,则a ≠ b”的第一步是 。
3、用反证法证明“如果一个三角形没有两个相等的角,那么这个三角形不是等腰三角形”的第一步
。
a不是实数
a小于或等于2
a大于或等于2
没有两个
一个也没有
两直线相交
假设a=b
假设这个三角形是等腰三角形
学力训练
4、在△ABC中,AB≠AC,求证:∠B ≠ ∠ C
A
B
C
证明:假设 ,
则 ( )
这与 矛盾.
假设不成立.
∴ .
∠B = ∠ C
AB=AC
等角对等边
已知AB≠AC
∠B ≠ ∠ C
小结:
反证法的步骤:假设结论的反面成立→逻辑推理得出矛盾→肯定原结论正确
感受反证法:
证明:假设a与b不止一个交点,不妨假设有两个交点A和A’。
因为两点确定一条直线,即经过点A和A’的直线有且只有一条,这与与已知两条直线矛盾,假设不成立。
所以两条直线相交只有一个交点。
小结:根据假设推出结论除了可以与已知条件矛盾以外,还可以与我们学过的定理、公理矛盾
5、求证:两条直线相交只有一个交点。
已知:如图两条相交直线a、b。
求证:a与b只有一个交点。
a
b
A
●
A,
●
1、求证:在一个三角形中,至少有一个内角小于或等于60°。
已知:△ABC
求证:△ABC中至少有一个内角小于或等于60°.
证明:假设 ,
则 。
∴ ,
即 。
这与 矛盾.假设不成立.
∴ .
△ABC中没有一个内角小于或等于60°
∠A>60°,∠B>60°,∠C>60°
∠A+∠B+∠C>180°
三角形的内角和为180度
△ABC中至少有一个内角小于或等于60°.
点拨:至少的反面是没有!
∠A+∠B+∠C>60°+60°+60°=180°
能力提升
2、求证:在同一平面内,如果一条直线和两条平行线中的一条相交,那么和另一条也相交.
已知:
直线l1, l2, l3在同一平面内,且l1∥l2, l3与l1相交于点P.
求证:
l3与l2相交.
证明:
假设____________,那么_________.
因为已知_________,
这与“_______________________ _____________”矛盾.
所以假设不成立,即求证的命题正确.
l1
l2
l3
P
l3与l2 不相交.
l3∥l2
l1∥l2
经过直线外一点,有且只有一条直线平行于已知直线
所以过直线l2外一点P,有两条直线和l2平行,
反证法的一般步骤:
假设命题结论不成立
假设不成立
假设命题结论反面成立
与已知条件矛盾
假设
推理得出的结论
与定理,定义,公理矛盾
所证命题成立
什么时候运用反证法呢?
课堂小结
14.1.3 反证法
教学目标
(1)1.通过实例,体会反证法的含义.
2.了解反证法的基本步骤,会用反证法证明简单的命题.
(2)通过利用反证法证明命题,体会逆向思维.
(3)在观察、操作、推理等探索过程中,体验数学活动充满探索性和创造性;渗透事物之间的相互对立、相互矛盾、相互转化的辩证唯物主义思想.
教学重难点
教学重点:运用反证法进行推理论证.
教学难点:理解“反证法”证明得出“矛盾的所在”.
一、问题情境
小华睡觉前,地上是干的,早晨起来,看见地上全湿了。小华对婷婷说:“昨天晚上下雨了。”
你能对小华的判断说出理由吗?
假设昨天晚上没有下雨,那么地上应是干的,这与早晨地上全湿了相矛盾,所以说昨晚下雨是正确的。
小华的理由:
我们可以把这种说理方法应用到数学问题上。
情景导入
解析:
由∠C=90°可知是直角三角形,根据勾股定理可知
a2 +b2 =c2 .
如图,在△ABC中,AB=c,BC=a,AC=b,如果∠C=90°,a、b、c三边有何关系?为什么?
A
C
C
a
b
c
复习回顾
探究:假设a2 +b2 =c2,由勾股定理可知三角形ABC是直角三角形,且∠C=90°,这与已知条件∠C≠90°矛盾。假设不成立,从而说明原结论a2 +b2 ≠ c2 成立。
A
C
C
若将上面的条件改为“在△ABC中,AB=c,BC=a, AC=b,∠C≠90°”,请问结论a2 +b2 ≠ c2 成立吗?请说明理由。
a
b
c
这种证明方法与前面的证明方法不同,它是首先假设结论的反面成立,然后经过正确的逻辑推理得出与已知、定理、公理矛盾的结论,从而得到原结论的正确。象这样的证明方法叫做反证法。
问题:
发现知识:
探究新知
1、试说出下列命题的反面:
(1)a是实数。 (2)a大于2。
(3)a小于2。 (4)至少有2个
(5)最多有一个 (6)两条直线平行。
2、用反证法证明“若a2≠ b2,则a ≠ b”的第一步是 。
3、用反证法证明“如果一个三角形没有两个相等的角,那么这个三角形不是等腰三角形”的第一步
。
a不是实数
a小于或等于2
a大于或等于2
没有两个
一个也没有
两直线相交
假设a=b
假设这个三角形是等腰三角形
学力训练
4、在△ABC中,AB≠AC,求证:∠B ≠ ∠ C
A
B
C
证明:假设 ,
则 ( )
这与 矛盾.
假设不成立.
∴ .
∠B = ∠ C
AB=AC
等角对等边
已知AB≠AC
∠B ≠ ∠ C
小结:
反证法的步骤:假设结论的反面成立→逻辑推理得出矛盾→肯定原结论正确
感受反证法:
证明:假设a与b不止一个交点,不妨假设有两个交点A和A’。
因为两点确定一条直线,即经过点A和A’的直线有且只有一条,这与与已知两条直线矛盾,假设不成立。
所以两条直线相交只有一个交点。
小结:根据假设推出结论除了可以与已知条件矛盾以外,还可以与我们学过的定理、公理矛盾
5、求证:两条直线相交只有一个交点。
已知:如图两条相交直线a、b。
求证:a与b只有一个交点。
a
b
A
●
A,
●
1、求证:在一个三角形中,至少有一个内角小于或等于60°。
已知:△ABC
求证:△ABC中至少有一个内角小于或等于60°.
证明:假设 ,
则 。
∴ ,
即 。
这与 矛盾.假设不成立.
∴ .
△ABC中没有一个内角小于或等于60°
∠A>60°,∠B>60°,∠C>60°
∠A+∠B+∠C>180°
三角形的内角和为180度
△ABC中至少有一个内角小于或等于60°.
点拨:至少的反面是没有!
∠A+∠B+∠C>60°+60°+60°=180°
能力提升
2、求证:在同一平面内,如果一条直线和两条平行线中的一条相交,那么和另一条也相交.
已知:
直线l1, l2, l3在同一平面内,且l1∥l2, l3与l1相交于点P.
求证:
l3与l2相交.
证明:
假设____________,那么_________.
因为已知_________,
这与“_______________________ _____________”矛盾.
所以假设不成立,即求证的命题正确.
l1
l2
l3
P
l3与l2 不相交.
l3∥l2
l1∥l2
经过直线外一点,有且只有一条直线平行于已知直线
所以过直线l2外一点P,有两条直线和l2平行,
反证法的一般步骤:
假设命题结论不成立
假设不成立
假设命题结论反面成立
与已知条件矛盾
假设
推理得出的结论
与定理,定义,公理矛盾
所证命题成立
什么时候运用反证法呢?
课堂小结
