14.2 勾股定理的应用 同步练习(含答案)
文档属性
| 名称 | 14.2 勾股定理的应用 同步练习(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 458.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 00:00:00 | ||
图片预览




文档简介
14.2 勾股定理的应用
一、单选题
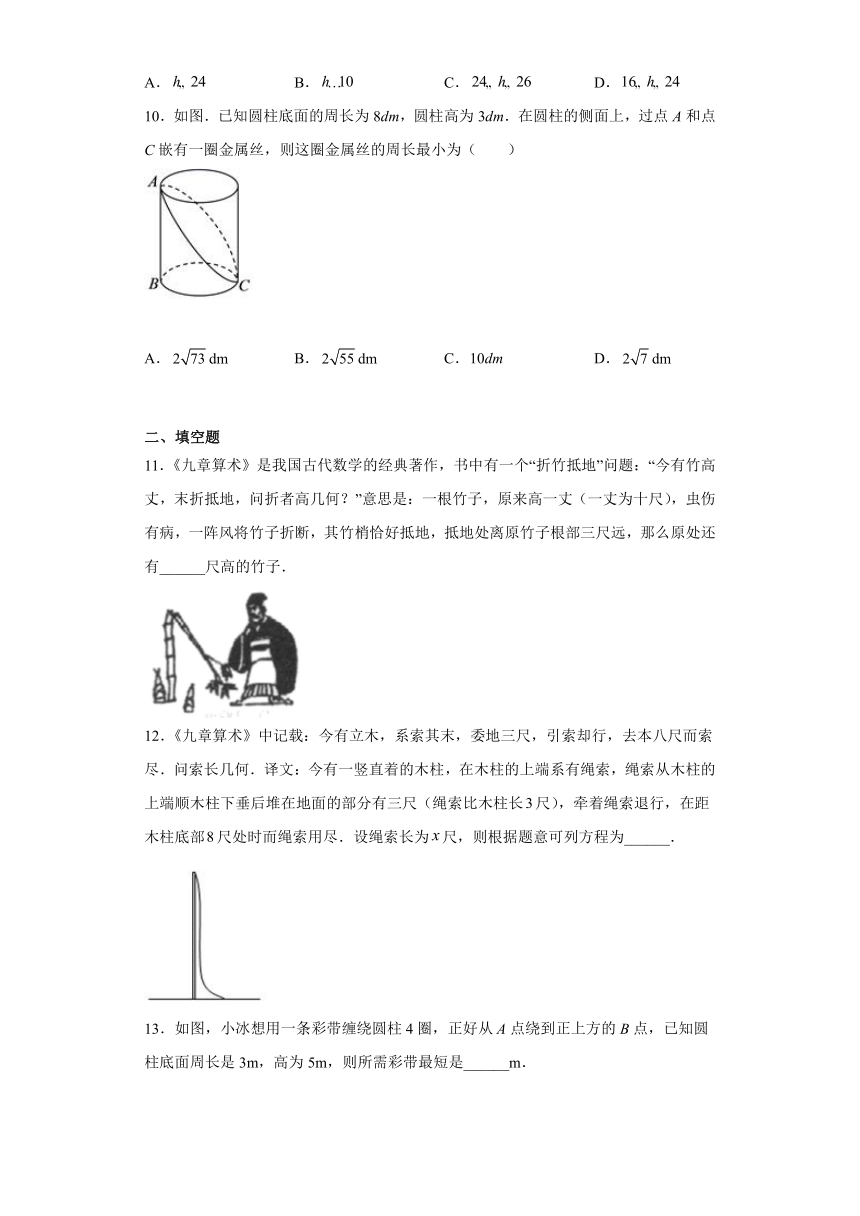
1.如图在Rt中,,,,在上截取,在上截取,在数轴上,为原点,则点对应的实数是( )
A. B. C. D.
2.如图,牧童在处放牛,牧童家在处,,处距河岸的距离、的长分别为5km和10km,且,两点的距离为8km,天黑前牧童从处将牛牵到河边饮水再回家,那么牧童最少要走的距离为( ).
A.15km B.16km C.17km D.18km
3.如图,在长方体透明容器(无盖)内的点处有一滴糖浆,容器外点处的蚂蚁想沿容器壁爬到容器内吃糖浆,已知容器长为,宽为,高为,点距底部,请问蚂蚁需爬行的最短距离是(容器壁厚度不计)( )
A. B. C. D.
4.如图,已知1号、4号两个正方形的面积和为10,2号、3号两个正方形的面积和为8,则a,b,c三个正方形的面积和为( )
A.18 B.26 C.28 D.34
5.一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端7米,消防车的云梯最大升长为25米,则云梯可以达该建筑物的最大高度是( )
A.16米 B.20米 C.24米 D.25米
6.如图有一个圆柱,它的高等于12cm,底面上圆的周长等于10cm,在圆柱下底面的点A有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱侧面爬行的最短路程是( )
A.2cm B.2cm C.10cm D.13cm
7.如图,长方体的长、宽、高分别是6,3,5,现一只蚂蚁从A点爬行到B点,设爬行的最短路线长为a,则的值是( )
A.130 B.106 C.100 D.86
8.如图,有一个水池,水面是一个边长为14尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.则水的深度是( )
A.15尺 B.24尺 C.25尺 D.28尺
9.如图,将一根长30cm的筷子,置于底面直径为10cm,高24cm的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为hcm,则h的取值范围是( )
A. B. C. D.
10.如图.已知圆柱底面的周长为8dm,圆柱高为3dm.在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为( )
A. B. C.10dm D.
二、填空题
11.《九章算术》是我国古代数学的经典著作,书中有一个“折竹抵地”问题:“今有竹高丈,末折抵地,问折者高几何?”意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,那么原处还有______尺高的竹子.
12.《九章算术》中记载:今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽.问索长几何.译文:今有一竖直着的木柱,在木柱的上端系有绳索,绳索从木柱的上端顺木柱下垂后堆在地面的部分有三尺(绳索比木柱长尺),牵着绳索退行,在距木柱底部尺处时而绳索用尽.设绳索长为尺,则根据题意可列方程为______.
13.如图,小冰想用一条彩带缠绕圆柱4圈,正好从A点绕到正上方的B点,已知圆柱底面周长是3m,高为5m,则所需彩带最短是______m.
14.一架云梯长25米,如图靠在墙上,云梯底端离墙15米,现把云梯顶端向上移4米,那么它的底端离墙________ 米.
15.如图,圆柱形玻璃杯高为5cm,底面周长为12cm,在杯内壁底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离是(杯壁厚度不计)_______.
三、解答题
16.如图,货船和快艇分别从码头A同时出发.其中,货船沿着北偏西54°方向以15海里/小时的速度匀速航行,快艇沿着北偏东36°方向以36海里/小时的速度航行,1小时后.两船分别到达B、C点.求B、C两点之间的距离.
17.笔直的河流一侧有一营地C,河边有两个漂流点A,B、其中AB=AC,由于周边施工,由C到A的路现在已经不通,为方便游客,在河边新建一个漂流点H(A,H,B在同一直线上),并新修一条路CH,测得BC=10千米,CH=8千米,BH=6千米.
(1)判断△BCH的形状,并说明理由;
(2)求原路线AC的长.
18.如图,AB、BC、CD、DE是四条长度均为5的线段,A,C,E共线,若AC=2,BC⊥CD,求线段CE的长度.
19.如图,铁路上A、D两点相距28km,B,C为两村庄,AB⊥AD于A,CD⊥AD于D,已知AB=16km,CD=12km,现在要在铁路AD上建一个土特产品收购站P,使得B、C两村到P站的距离相等,则P站应建在距点A多少千米处?
20.如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 多少cm?
21.如图,一个长为15m的梯子AB斜靠在墙上,梯子的顶端距地面的距离为12m,若梯子的顶端下滑的距离与梯子的底端向后滑动的距离相等,求梯子顶端下滑的距离是多少m?
22.吴老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题,请你根据下列所给的条件分别求出蚂蚁需要爬行的最短路径长.
(1)如图1,正方体的棱长为5cm,一只蚂蚁欲从正方体底面上的点A沿正方体表面爬到点C1处;
(2)如图2,长方体底面是边长为5cm的正方形,高为6cm,一只蚂蚁欲从长方体底面上的点A沿长方体表而爬到点C1处;
(3)如图3,是一个底面周长为10cm,高为5cm的圆柱体,一只蚂蚁欲从圆柱体底面上的点A沿圆柱体侧面爬到点C处.
23.在中,,,点为直线上一动点,连接,将线段绕点逆时针旋转,得到线段,连接.
(1)如图1,当时,请直接写出线段和线段之间的数量关系;
(2)如图2,当时,其它条件不变,试判断线段、、的数量关系,并证明;
参考答案
1.A
2.C
3.D
4.B
5.C
6.D
7.C
8.B
9.C
10.C
11.
12.
13.13
14.7
15.10
16.B、C两点之间的距离为海里
17.(1)△HBC是直角三角形,理由见解析;(2)原来的路线AC的长为千米.
18.
19.站应建在距点千米处.
20.15cm
21.梯子顶端下滑的距离是3米.
22.(1)蚂蚁需要爬行的最短路径长为cm;(2)蚂蚁需要爬行的最短路径长为cm;(3)蚂蚁需要爬行的最短路径长为cm.
23.(1);(2)
一、单选题
1.如图在Rt中,,,,在上截取,在上截取,在数轴上,为原点,则点对应的实数是( )
A. B. C. D.
2.如图,牧童在处放牛,牧童家在处,,处距河岸的距离、的长分别为5km和10km,且,两点的距离为8km,天黑前牧童从处将牛牵到河边饮水再回家,那么牧童最少要走的距离为( ).
A.15km B.16km C.17km D.18km
3.如图,在长方体透明容器(无盖)内的点处有一滴糖浆,容器外点处的蚂蚁想沿容器壁爬到容器内吃糖浆,已知容器长为,宽为,高为,点距底部,请问蚂蚁需爬行的最短距离是(容器壁厚度不计)( )
A. B. C. D.
4.如图,已知1号、4号两个正方形的面积和为10,2号、3号两个正方形的面积和为8,则a,b,c三个正方形的面积和为( )
A.18 B.26 C.28 D.34
5.一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端7米,消防车的云梯最大升长为25米,则云梯可以达该建筑物的最大高度是( )
A.16米 B.20米 C.24米 D.25米
6.如图有一个圆柱,它的高等于12cm,底面上圆的周长等于10cm,在圆柱下底面的点A有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱侧面爬行的最短路程是( )
A.2cm B.2cm C.10cm D.13cm
7.如图,长方体的长、宽、高分别是6,3,5,现一只蚂蚁从A点爬行到B点,设爬行的最短路线长为a,则的值是( )
A.130 B.106 C.100 D.86
8.如图,有一个水池,水面是一个边长为14尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.则水的深度是( )
A.15尺 B.24尺 C.25尺 D.28尺
9.如图,将一根长30cm的筷子,置于底面直径为10cm,高24cm的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为hcm,则h的取值范围是( )
A. B. C. D.
10.如图.已知圆柱底面的周长为8dm,圆柱高为3dm.在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为( )
A. B. C.10dm D.
二、填空题
11.《九章算术》是我国古代数学的经典著作,书中有一个“折竹抵地”问题:“今有竹高丈,末折抵地,问折者高几何?”意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,那么原处还有______尺高的竹子.
12.《九章算术》中记载:今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽.问索长几何.译文:今有一竖直着的木柱,在木柱的上端系有绳索,绳索从木柱的上端顺木柱下垂后堆在地面的部分有三尺(绳索比木柱长尺),牵着绳索退行,在距木柱底部尺处时而绳索用尽.设绳索长为尺,则根据题意可列方程为______.
13.如图,小冰想用一条彩带缠绕圆柱4圈,正好从A点绕到正上方的B点,已知圆柱底面周长是3m,高为5m,则所需彩带最短是______m.
14.一架云梯长25米,如图靠在墙上,云梯底端离墙15米,现把云梯顶端向上移4米,那么它的底端离墙________ 米.
15.如图,圆柱形玻璃杯高为5cm,底面周长为12cm,在杯内壁底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离是(杯壁厚度不计)_______.
三、解答题
16.如图,货船和快艇分别从码头A同时出发.其中,货船沿着北偏西54°方向以15海里/小时的速度匀速航行,快艇沿着北偏东36°方向以36海里/小时的速度航行,1小时后.两船分别到达B、C点.求B、C两点之间的距离.
17.笔直的河流一侧有一营地C,河边有两个漂流点A,B、其中AB=AC,由于周边施工,由C到A的路现在已经不通,为方便游客,在河边新建一个漂流点H(A,H,B在同一直线上),并新修一条路CH,测得BC=10千米,CH=8千米,BH=6千米.
(1)判断△BCH的形状,并说明理由;
(2)求原路线AC的长.
18.如图,AB、BC、CD、DE是四条长度均为5的线段,A,C,E共线,若AC=2,BC⊥CD,求线段CE的长度.
19.如图,铁路上A、D两点相距28km,B,C为两村庄,AB⊥AD于A,CD⊥AD于D,已知AB=16km,CD=12km,现在要在铁路AD上建一个土特产品收购站P,使得B、C两村到P站的距离相等,则P站应建在距点A多少千米处?
20.如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 多少cm?
21.如图,一个长为15m的梯子AB斜靠在墙上,梯子的顶端距地面的距离为12m,若梯子的顶端下滑的距离与梯子的底端向后滑动的距离相等,求梯子顶端下滑的距离是多少m?
22.吴老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题,请你根据下列所给的条件分别求出蚂蚁需要爬行的最短路径长.
(1)如图1,正方体的棱长为5cm,一只蚂蚁欲从正方体底面上的点A沿正方体表面爬到点C1处;
(2)如图2,长方体底面是边长为5cm的正方形,高为6cm,一只蚂蚁欲从长方体底面上的点A沿长方体表而爬到点C1处;
(3)如图3,是一个底面周长为10cm,高为5cm的圆柱体,一只蚂蚁欲从圆柱体底面上的点A沿圆柱体侧面爬到点C处.
23.在中,,,点为直线上一动点,连接,将线段绕点逆时针旋转,得到线段,连接.
(1)如图1,当时,请直接写出线段和线段之间的数量关系;
(2)如图2,当时,其它条件不变,试判断线段、、的数量关系,并证明;
参考答案
1.A
2.C
3.D
4.B
5.C
6.D
7.C
8.B
9.C
10.C
11.
12.
13.13
14.7
15.10
16.B、C两点之间的距离为海里
17.(1)△HBC是直角三角形,理由见解析;(2)原来的路线AC的长为千米.
18.
19.站应建在距点千米处.
20.15cm
21.梯子顶端下滑的距离是3米.
22.(1)蚂蚁需要爬行的最短路径长为cm;(2)蚂蚁需要爬行的最短路径长为cm;(3)蚂蚁需要爬行的最短路径长为cm.
23.(1);(2)
