3.1.2 函数的表示法 练习-2022-2023学年高一上学期数学人教A版(2019)必修第一册(含答案)
文档属性
| 名称 | 3.1.2 函数的表示法 练习-2022-2023学年高一上学期数学人教A版(2019)必修第一册(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 541.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-24 00:00:00 | ||
图片预览




文档简介
3.1.2函数的表示法
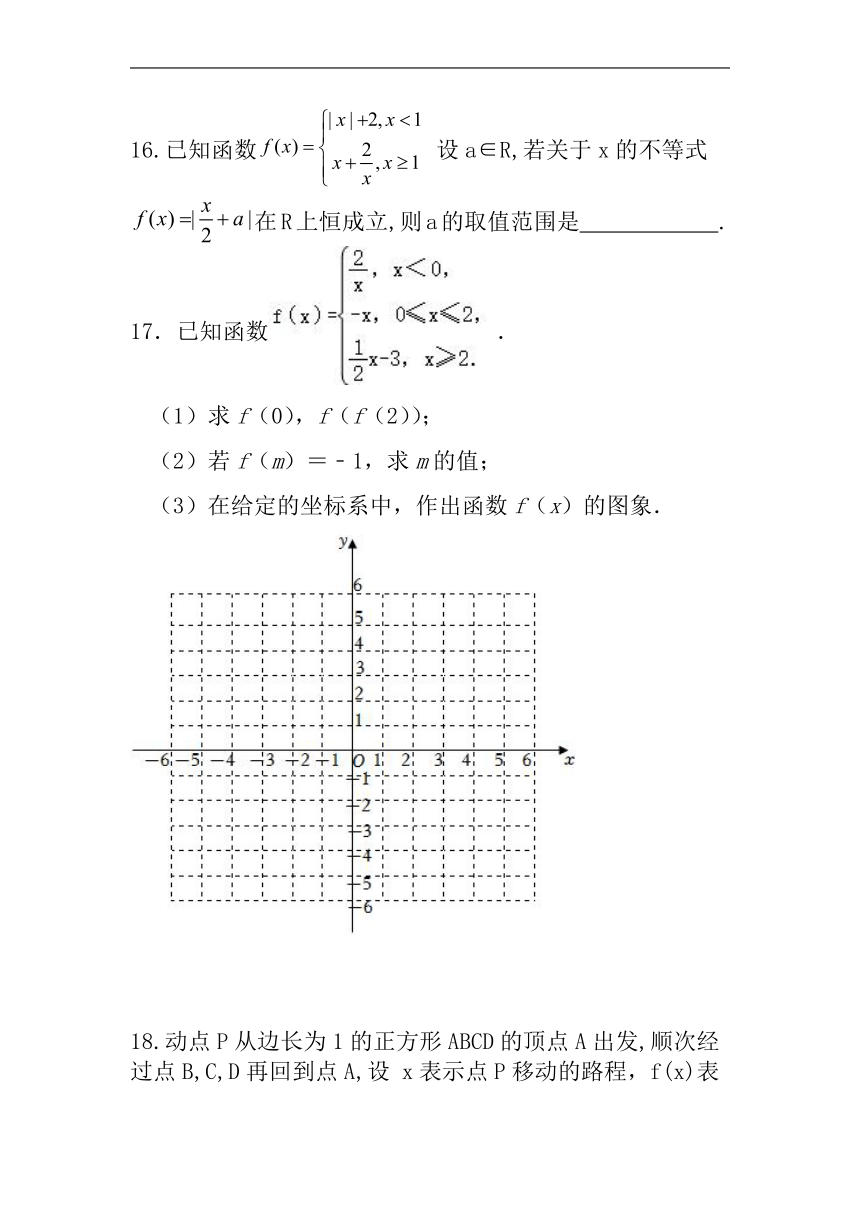
1.函数的图像是( )
A. B.
C. D.
2.已知函数,则的值为( )
A. B. C. D.
3.设f(x)=则使得f(m)=1成立的m值是( )
A.10 B.0或10 C.0或﹣2或10 D.1或﹣1或11
4.已知函数f(x)和g(x)分别由表给出,则满足f(g(x))>g(f(x))的x的取值范围是( )
x 1 2 3
f(x) 1 3 2
x 1 2 3
g(x) 2 1 3
{1,2,3} B.{1,2} C.{1,3} D.{1}
5.已知函数,则函数f(x)的图像是( )
已知函数f(x)=3x-1,若f(g(x))=2x+3,则函数g(x)的解析式为( )
7.设函数f(x)的定义域为R,满足f(x+1)=2f(x),且当x∈(0,1]时,f(x)=x(x-1).若对任意x∈(-∞,m],都有f(x)≥-,则m的取值范围是( )
A. B. C. D.
8.已知,则不等式xf(x)+x≤2的解集为( )
A. [0,1] B. [0,2] C.(-∞,1] D.(-∞,2]
9.(多选题)已知函数y=f(x)用列表法表示如表,若f(f(x))=x﹣1,则x可取( )
x 1 2 3 4 5
f(x) 2 3 4 2 3
A.2 B.3 C.4 D.5
10.(多选题)下列给出的函数是分段函数的是( )
A. B.
C. D.
11.(多选题)高斯是十八世纪德国著名数学家、物理学家、天文学家,是近代数学奠基者之一,享有“数学王子”之称.,[x]表示不超过x的最大整数.函数y=[x]称为高斯函数,人们更习惯称为“取整函数”,则下列命题中的真命题是( )
A.
B.
C.函数y=x-[x] (x∈R)的值域为[0,1)
12.(多选题)设函数y=f(x)的定义域为R,对于任一给定的正数p,定义函数,则称函数fp(x)为f(x)的“p界函数”若给定函数f(x)=x2-2x-1,p=2,则下列结论成立的是( )
fp(f(0))=f(fp(0)) B.fp(f(1))=f(fp(1))
f(f(2))=fp(fp(2)) D.f(f(3))=fp(fp(3))
13.已知函数 的值域为[0,+∞),则m的取值范围是_____.
14.已知函数f(x)的图象如图所示,其中y轴的左侧为一条线段,
右侧为某抛物线的一段.则函数f(x)= .
15.若方程 x2-4|x|+3=m有四个互不相等的实数根,则 m的取值范围是 .
16.已知函数 设a∈R,若关于x的不等式在R上恒成立,则a的取值范围是 .
17.已知函数.
(1)求f(0),f(f(2));
(2)若f(m)=﹣1,求m的值;
(3)在给定的坐标系中,作出函数f(x)的图象.
18.动点P从边长为1的正方形ABCD的顶点A出发,顺次经过点B,C,D再回到点A,设 x表示点P移动的路程,f(x)表示线段PA的长,g(x)表示△ABP的面积,求f(x)和 g(x),并作出g(x)的简图.
19.(1)已知一次函数f(x)满足f(f(x))=9x+7 求f(x)的解析式。
(2)已知二次函数f(x)满足f(0)=1,f(1)=2,f(2)=5, 求该二次函数的解析式 。
(3)已知,求f(x)的解析式。
(4)已知函数 f(x+1)= x -2x,求f(x)的解析式。
(5)已知函数f(x)满足,求函数f(x)的解析式。
(6)已知af(x) +f(-x)=bx,其中a≠±1,求函数f(x)的解析式。
20.某公司共有60位员工,为提高员工的业务技术水平,公司拟聘请专业培训机构对其进行培训.培训的总费用由两部分组成:一部分是给每位参加培训的员工支付400元的培训材料费;另一部分是给培训机构交纳的培训费.若参加培训的员工人数不超过30,则每人收取培训费1000元;若参加培训的员工人数超过30,则每超过1人,人均培训费减少20元.设公司参加培训的员工人数为x,此次培训的总费用为y元.
(1)求y与x之间的函数关系式;
(2)当参加培训的员工人数是50时,所需的总费用是多少元
已知对于一切正整数n,都有,存在实数a使f3(a)=f6(a),求f28(a).
3.1.2函数的表示法答案
1~5 CBCCA 6~8 ABC 9 BCD 10 AD 11 BCD 12 ACD
13 [4,+∞) 14 f(x)=
(-1,3) 16 [-2,2]
【解析】
1.C 【解答】解:函数
作出函数图象为:
故选:C.
2.B【解答】解:∵已知函数,
∴ 故选:B.
3.C【解答】解:当m<1时,f(m)=(m+1)2=1
∴m=﹣2或m=0
当m≥1时,f(m)=4﹣=1 ∴m=10
综上:m的取值为:﹣2,0,10 故选:C.
4.C【解答】解:根据题意,函数的定义域为{1,2,3},
当x=1时,f(g(1))=f(2)=3,g(f(1))=g(1)=2,f(g(x))>g(f(x))成立;
当x=2时,f(g(2))=f(1)=1,g(f(2))=g(3)=3,f(g(x))>g(f(x))不成立;
当x=3时,f(g(3))=f(3)=2,g(f(3))=g(2)=1,f(g(x))>g(f(x))成立;
故满足f(g(x))>g(f(x))的x的取值范围是{1,3};故选:C.
5.A【解答】解:因为
x=-1时,y=0,即图像过(-1,0)D错
当x=0时,y=1,即图像过(0,1)C错
当x=1时,y=2,即图像过(1,2)B错;故选A
6.A【解答】解:因为f(g(x))=3g(x)-1=2x+3,所以3g(x)=2x+4,则
B【解答】解:当-1当1当2由此可得
作出函数f(x)的图像并画出y= -,如图所示
由图可知当2C【解答】解: 当x≥0时,x×1+x≤2,解得0≤x≤1;
当x<0时,x≤2,所以x<0.所以不等式 xf(x) +x≤2 的解集为(-∞,1],故选C
BCD 【解答】解:结合表格可知,
当x=1时,f(1)=2,则f(f(1))=f(2)=3≠1﹣1=0,
当x=2时,f(2)=3,f(f(2)=f(3)=4≠2﹣1;
当x=3时,f(3)=4,f(f(3))=f(4)=2=3﹣1,此时满足题意;
当x=4时,f(4)=2,f(f(4))=f(2)=3=4﹣1,此时满足题意;
当x=5时,f(5)=3,f(f(5))=f(3)=4=5﹣1,此时满足题意.
故选:BCD.
10.AD 【解答】解:是分段函数的解析式,正确;
因为不满足函数的定义,不是函数的解析式,所以B不正确;
不满足函数的定义,不是函数的解析式,所以C不正确;
满足函数的定义,是分段函数的解析式,所以D正确;故选:AD.
11.BCD 【解答】解:[x]是整数,若x≥[x] +1,[x] +1是数,∴[x]≥[x]+1,矛盾,∴A错误
x,y∈R, [x]≤x, [y]≤y,∴[x]+[y]≤x+y,∴[x]+[y]≤[x+y],B正确;
由定义知,x-1<[x]≤x,∴0≤x-[x]<1,∴函数f(x) =x-[x]的值域是[0,1),C正确;
若使得[t3]=1, [t4]=2 ,[t5] =3,…, [tn]=n-2同时成立,则, , , 同时成立,,当n≥6时,则不存在t同时满足,, 只有n≤5时,存在满足题意,D正确.故选 BCD.
ACD 【解答】解: 由题意知,
当f(x)=x2-2x-1,p=2时,有
作y=f(x)及y=fp(x)的图象,如
由图可知,f(0)= -1, fp(f(0))=fp(-1)=2, fp(0)= -1, J,(0))=f(-1)=2, f(fp(0))=f(-1)=2故A成立.
同理fp(f(1))=fp(-2)=2, f(fp(1))=f(-2)=7,故B不成立.
f(f(2))=f(-1)=2, fp(fp(2))=fp(-1)=2,故C成立.
f(f(3))=f(2)=-1, fp(fp(3))=fp(2)=-1,故D成立.
[4,+∞ )【解答】解: 当m=0时,f(x)=1不符合题意;当m≠0时,令 g(x)=mx2+mx+1则g(x)的图象需开口向上且与x轴有交点,所以解得m≥4,则m的取值范围是[4,+∞ )
14.【解答】解:当x∈[﹣2,0]时,设f(x)=kx+b(k≠0),
将(﹣2,0),(0,2)代入可得,解得k=1,b=2,
即f(x)=x+2,
当x∈(0,3]时,设f(x)=a(x﹣2)2﹣2,将点(3,﹣1)代入可得
﹣1=a(3﹣2)2﹣2,解得a=1,
∴f(x)=(x﹣2)2﹣2=x2﹣4x+2,
∴f(x)=.故答案为:
15. (-1,3) 【详解】解:作出 的函数图象如图所示:
方程x2-4|x|+3=m有四个互不相等的实数根,
所以,直线y=m与y=x2-4|x|+3的函数图象有4个交点,当x=2时,y=-1; x=0时,y=3, -116. [-2,2] 【详解】解:首先画出函数f(x)的图像,当的图像经过(0,2)时,可知,当 的图像与的图像相切时,由,得x2-2ax+4=0,由,并结合图像可得a=2,要使恒成立,当a≤0时,需满足-a≤2,即-2≤a≤0,当a>0时,需满足a≤2,所以-2≤a≤2
17.【解答】解:(1)∵函数,
∴f(0)=0,f(2)=×2﹣3=﹣2,则f(f(2))=f(﹣2)==﹣1;
(2)当m<0时,f(m)==﹣1,解得m=﹣2;
当0≤m≤2时,f(m)=﹣m=﹣1,解得m=1;
当m≥2时,f(m)=m﹣3=﹣1,解得m=4,
综上所述,m的值为﹣2或1或4;
(3)函数f(x)的图象,如图所示:
【解答】解:如图18.1所示,当P在AB上运动时,PA=x;当点P在BC上运动时,由RtABP可得;当点P在CD上运动时,由RtΔADP 易得 ;当点P在DA上运动时,PA=4-x,故f(x)的表达式为:
图18.1
由于点P在正方形ABCD上不同位置时,△ABP的面积也不同,因此必须对点P的位置进行分类讨论:
如图18.1,当点P在AB上,即0≤x≤1时,△ABP的面积;当点P在BC上,即1故
图18.2
g(x)的简图如图 18.2所示.
19.【解答】解:(1)设f(x) =ax +b(a≠0),则f(f(x)) = f(ax +6) =a(ax +6) +b =a2x +ab +b =9x +7,于是有解得,所以
f(x) =3x + 或f(x) = -2x -.
设该二次函数的解析式为f(x) =ax2+bx+c(a≠0),由题意得 解得,故f(x) =x2 +1.
方法一(换元法) 令,则x=(t-1) ,所以f(t) =(t-1) +2(t-1) =t2-1(t≥1),所以函数f(x)的解析式为f(x) =x2-1(x≥1).
方法二(配凑法)
因为所以函数f(x)的解析式为f(x) = x -1(x≥1).
方法一(换元法) 令x+1=t,则x=t-1,t∈R,所以f(t)=(t-1)2-2(t-1)=t2-4t +3,即f(x) =x -4x +3.
方法二(配凑法) 因为x2-2x=(x2+2x+1)-(4x+4)+3=(x+1)2-4(x+1)+3,所以f(x+1)=(x+1)2-4(x+1)+3,即f(x) =x2-4x +3.
在已知等式中,将x换成,得,与已知方程联立,得消去f(),得
在原式中以 -x 替换 x,得 af(-x) + f(x)=-bx,于是得,
消去f(-x)得.
故函数f(x)的解析式。
20.【解答】解:(1)当0≤x≤30,x∈N时,y=400x+1000x =1 400x;
当30故
(2)当x=50时y=-20×502+2000×50=50000
所以当参加培训的员工人数是50时,所需的总费用是50000元 .
21.【解答】解:得所以对于一切正整数n,当n为奇数时,当n为偶数时.
所以.
由,解得
所以
1.函数的图像是( )
A. B.
C. D.
2.已知函数,则的值为( )
A. B. C. D.
3.设f(x)=则使得f(m)=1成立的m值是( )
A.10 B.0或10 C.0或﹣2或10 D.1或﹣1或11
4.已知函数f(x)和g(x)分别由表给出,则满足f(g(x))>g(f(x))的x的取值范围是( )
x 1 2 3
f(x) 1 3 2
x 1 2 3
g(x) 2 1 3
{1,2,3} B.{1,2} C.{1,3} D.{1}
5.已知函数,则函数f(x)的图像是( )
已知函数f(x)=3x-1,若f(g(x))=2x+3,则函数g(x)的解析式为( )
7.设函数f(x)的定义域为R,满足f(x+1)=2f(x),且当x∈(0,1]时,f(x)=x(x-1).若对任意x∈(-∞,m],都有f(x)≥-,则m的取值范围是( )
A. B. C. D.
8.已知,则不等式xf(x)+x≤2的解集为( )
A. [0,1] B. [0,2] C.(-∞,1] D.(-∞,2]
9.(多选题)已知函数y=f(x)用列表法表示如表,若f(f(x))=x﹣1,则x可取( )
x 1 2 3 4 5
f(x) 2 3 4 2 3
A.2 B.3 C.4 D.5
10.(多选题)下列给出的函数是分段函数的是( )
A. B.
C. D.
11.(多选题)高斯是十八世纪德国著名数学家、物理学家、天文学家,是近代数学奠基者之一,享有“数学王子”之称.,[x]表示不超过x的最大整数.函数y=[x]称为高斯函数,人们更习惯称为“取整函数”,则下列命题中的真命题是( )
A.
B.
C.函数y=x-[x] (x∈R)的值域为[0,1)
12.(多选题)设函数y=f(x)的定义域为R,对于任一给定的正数p,定义函数,则称函数fp(x)为f(x)的“p界函数”若给定函数f(x)=x2-2x-1,p=2,则下列结论成立的是( )
fp(f(0))=f(fp(0)) B.fp(f(1))=f(fp(1))
f(f(2))=fp(fp(2)) D.f(f(3))=fp(fp(3))
13.已知函数 的值域为[0,+∞),则m的取值范围是_____.
14.已知函数f(x)的图象如图所示,其中y轴的左侧为一条线段,
右侧为某抛物线的一段.则函数f(x)= .
15.若方程 x2-4|x|+3=m有四个互不相等的实数根,则 m的取值范围是 .
16.已知函数 设a∈R,若关于x的不等式在R上恒成立,则a的取值范围是 .
17.已知函数.
(1)求f(0),f(f(2));
(2)若f(m)=﹣1,求m的值;
(3)在给定的坐标系中,作出函数f(x)的图象.
18.动点P从边长为1的正方形ABCD的顶点A出发,顺次经过点B,C,D再回到点A,设 x表示点P移动的路程,f(x)表示线段PA的长,g(x)表示△ABP的面积,求f(x)和 g(x),并作出g(x)的简图.
19.(1)已知一次函数f(x)满足f(f(x))=9x+7 求f(x)的解析式。
(2)已知二次函数f(x)满足f(0)=1,f(1)=2,f(2)=5, 求该二次函数的解析式 。
(3)已知,求f(x)的解析式。
(4)已知函数 f(x+1)= x -2x,求f(x)的解析式。
(5)已知函数f(x)满足,求函数f(x)的解析式。
(6)已知af(x) +f(-x)=bx,其中a≠±1,求函数f(x)的解析式。
20.某公司共有60位员工,为提高员工的业务技术水平,公司拟聘请专业培训机构对其进行培训.培训的总费用由两部分组成:一部分是给每位参加培训的员工支付400元的培训材料费;另一部分是给培训机构交纳的培训费.若参加培训的员工人数不超过30,则每人收取培训费1000元;若参加培训的员工人数超过30,则每超过1人,人均培训费减少20元.设公司参加培训的员工人数为x,此次培训的总费用为y元.
(1)求y与x之间的函数关系式;
(2)当参加培训的员工人数是50时,所需的总费用是多少元
已知对于一切正整数n,都有,存在实数a使f3(a)=f6(a),求f28(a).
3.1.2函数的表示法答案
1~5 CBCCA 6~8 ABC 9 BCD 10 AD 11 BCD 12 ACD
13 [4,+∞) 14 f(x)=
(-1,3) 16 [-2,2]
【解析】
1.C 【解答】解:函数
作出函数图象为:
故选:C.
2.B【解答】解:∵已知函数,
∴ 故选:B.
3.C【解答】解:当m<1时,f(m)=(m+1)2=1
∴m=﹣2或m=0
当m≥1时,f(m)=4﹣=1 ∴m=10
综上:m的取值为:﹣2,0,10 故选:C.
4.C【解答】解:根据题意,函数的定义域为{1,2,3},
当x=1时,f(g(1))=f(2)=3,g(f(1))=g(1)=2,f(g(x))>g(f(x))成立;
当x=2时,f(g(2))=f(1)=1,g(f(2))=g(3)=3,f(g(x))>g(f(x))不成立;
当x=3时,f(g(3))=f(3)=2,g(f(3))=g(2)=1,f(g(x))>g(f(x))成立;
故满足f(g(x))>g(f(x))的x的取值范围是{1,3};故选:C.
5.A【解答】解:因为
x=-1时,y=0,即图像过(-1,0)D错
当x=0时,y=1,即图像过(0,1)C错
当x=1时,y=2,即图像过(1,2)B错;故选A
6.A【解答】解:因为f(g(x))=3g(x)-1=2x+3,所以3g(x)=2x+4,则
B【解答】解:当-1
作出函数f(x)的图像并画出y= -,如图所示
由图可知当2
当x<0时,x≤2,所以x<0.所以不等式 xf(x) +x≤2 的解集为(-∞,1],故选C
BCD 【解答】解:结合表格可知,
当x=1时,f(1)=2,则f(f(1))=f(2)=3≠1﹣1=0,
当x=2时,f(2)=3,f(f(2)=f(3)=4≠2﹣1;
当x=3时,f(3)=4,f(f(3))=f(4)=2=3﹣1,此时满足题意;
当x=4时,f(4)=2,f(f(4))=f(2)=3=4﹣1,此时满足题意;
当x=5时,f(5)=3,f(f(5))=f(3)=4=5﹣1,此时满足题意.
故选:BCD.
10.AD 【解答】解:是分段函数的解析式,正确;
因为不满足函数的定义,不是函数的解析式,所以B不正确;
不满足函数的定义,不是函数的解析式,所以C不正确;
满足函数的定义,是分段函数的解析式,所以D正确;故选:AD.
11.BCD 【解答】解:[x]是整数,若x≥[x] +1,[x] +1是数,∴[x]≥[x]+1,矛盾,∴A错误
x,y∈R, [x]≤x, [y]≤y,∴[x]+[y]≤x+y,∴[x]+[y]≤[x+y],B正确;
由定义知,x-1<[x]≤x,∴0≤x-[x]<1,∴函数f(x) =x-[x]的值域是[0,1),C正确;
若使得[t3]=1, [t4]=2 ,[t5] =3,…, [tn]=n-2同时成立,则, , , 同时成立,,当n≥6时,则不存在t同时满足,, 只有n≤5时,存在满足题意,D正确.故选 BCD.
ACD 【解答】解: 由题意知,
当f(x)=x2-2x-1,p=2时,有
作y=f(x)及y=fp(x)的图象,如
由图可知,f(0)= -1, fp(f(0))=fp(-1)=2, fp(0)= -1, J,(0))=f(-1)=2, f(fp(0))=f(-1)=2故A成立.
同理fp(f(1))=fp(-2)=2, f(fp(1))=f(-2)=7,故B不成立.
f(f(2))=f(-1)=2, fp(fp(2))=fp(-1)=2,故C成立.
f(f(3))=f(2)=-1, fp(fp(3))=fp(2)=-1,故D成立.
[4,+∞ )【解答】解: 当m=0时,f(x)=1不符合题意;当m≠0时,令 g(x)=mx2+mx+1则g(x)的图象需开口向上且与x轴有交点,所以解得m≥4,则m的取值范围是[4,+∞ )
14.【解答】解:当x∈[﹣2,0]时,设f(x)=kx+b(k≠0),
将(﹣2,0),(0,2)代入可得,解得k=1,b=2,
即f(x)=x+2,
当x∈(0,3]时,设f(x)=a(x﹣2)2﹣2,将点(3,﹣1)代入可得
﹣1=a(3﹣2)2﹣2,解得a=1,
∴f(x)=(x﹣2)2﹣2=x2﹣4x+2,
∴f(x)=.故答案为:
15. (-1,3) 【详解】解:作出 的函数图象如图所示:
方程x2-4|x|+3=m有四个互不相等的实数根,
所以,直线y=m与y=x2-4|x|+3的函数图象有4个交点,当x=2时,y=-1; x=0时,y=3, -1
17.【解答】解:(1)∵函数,
∴f(0)=0,f(2)=×2﹣3=﹣2,则f(f(2))=f(﹣2)==﹣1;
(2)当m<0时,f(m)==﹣1,解得m=﹣2;
当0≤m≤2时,f(m)=﹣m=﹣1,解得m=1;
当m≥2时,f(m)=m﹣3=﹣1,解得m=4,
综上所述,m的值为﹣2或1或4;
(3)函数f(x)的图象,如图所示:
【解答】解:如图18.1所示,当P在AB上运动时,PA=x;当点P在BC上运动时,由RtABP可得;当点P在CD上运动时,由RtΔADP 易得 ;当点P在DA上运动时,PA=4-x,故f(x)的表达式为:
图18.1
由于点P在正方形ABCD上不同位置时,△ABP的面积也不同,因此必须对点P的位置进行分类讨论:
如图18.1,当点P在AB上,即0≤x≤1时,△ABP的面积;当点P在BC上,即1
图18.2
g(x)的简图如图 18.2所示.
19.【解答】解:(1)设f(x) =ax +b(a≠0),则f(f(x)) = f(ax +6) =a(ax +6) +b =a2x +ab +b =9x +7,于是有解得,所以
f(x) =3x + 或f(x) = -2x -.
设该二次函数的解析式为f(x) =ax2+bx+c(a≠0),由题意得 解得,故f(x) =x2 +1.
方法一(换元法) 令,则x=(t-1) ,所以f(t) =(t-1) +2(t-1) =t2-1(t≥1),所以函数f(x)的解析式为f(x) =x2-1(x≥1).
方法二(配凑法)
因为所以函数f(x)的解析式为f(x) = x -1(x≥1).
方法一(换元法) 令x+1=t,则x=t-1,t∈R,所以f(t)=(t-1)2-2(t-1)=t2-4t +3,即f(x) =x -4x +3.
方法二(配凑法) 因为x2-2x=(x2+2x+1)-(4x+4)+3=(x+1)2-4(x+1)+3,所以f(x+1)=(x+1)2-4(x+1)+3,即f(x) =x2-4x +3.
在已知等式中,将x换成,得,与已知方程联立,得消去f(),得
在原式中以 -x 替换 x,得 af(-x) + f(x)=-bx,于是得,
消去f(-x)得.
故函数f(x)的解析式。
20.【解答】解:(1)当0≤x≤30,x∈N时,y=400x+1000x =1 400x;
当30
(2)当x=50时y=-20×502+2000×50=50000
所以当参加培训的员工人数是50时,所需的总费用是50000元 .
21.【解答】解:得所以对于一切正整数n,当n为奇数时,当n为偶数时.
所以.
由,解得
所以
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
