2022-2023学年华师大版数学八年级上册 13.2.2 全等三角形的判定条件 课件(共13张PPT)
文档属性
| 名称 | 2022-2023学年华师大版数学八年级上册 13.2.2 全等三角形的判定条件 课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 116.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-24 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
13.2.2 全等三角形的判定条件
教学目标
1.理解全等三角形及相关概念,能够从图形中寻找全等三角形,探索并掌握全等三角形的性质,能够利用性质解决简单的问题,以及对两个三角形全等的条件的探索
2.在探索全等三角形性质与三角形全等的条件的过程中,体会研究问题的方法,感受图形变化.
3.培养学生的分类讨论、归纳总结能力和应用意识.培养学生仔细认真的学习态度。
新课引入
1、请同学们观察下面的图形,看你有什么发现没有?
发现这两个图形可以完全重合。
像这样可以互相重合的两个图形,我们把他叫做——全等形。
那么这两个五角星我们就叫做全等五角星。
全等图形既包括规则图形,也包括不规则图形。
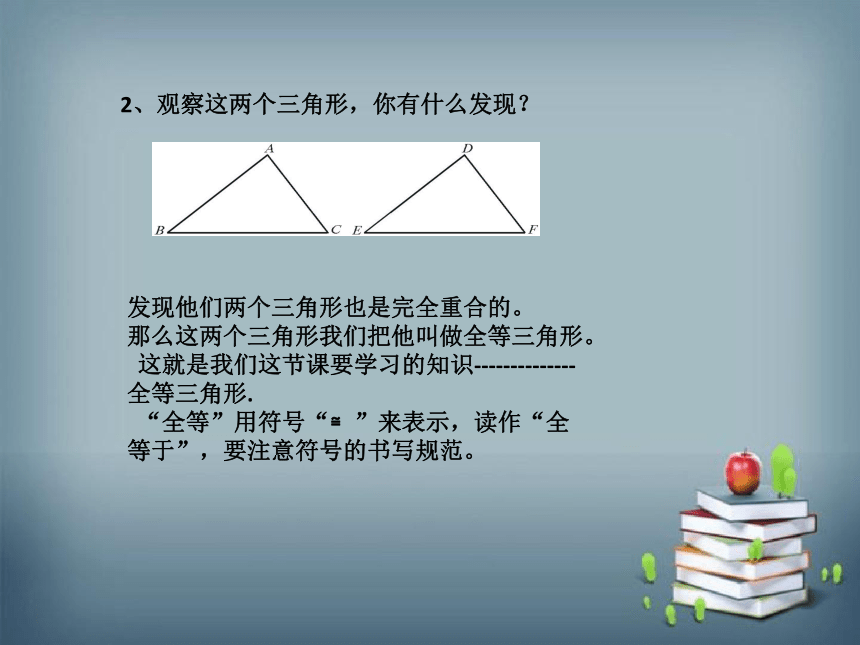
2、观察这两个三角形,你有什么发现?
发现他们两个三角形也是完全重合的。
那么这两个三角形我们把他叫做全等三角形。
这就是我们这节课要学习的知识--------------全等三角形.
“全等”用符号“≌”来表示,读作“全等于”,要注意符号的书写规范。
那么怎么用数学语言来表示这两个三角形全等呢?
△ABC ≌ △DEF
这时,点A与点D重合.点B与点E重合.我们把这样互相重合的一对点叫做对应顶点;AB边与DE边重合,这样互相重合的边就叫做对应边;∠A与∠D重合,它们就是对应角.△ABC与△DEF全等,我们把它记作:“△ABC≌△DEF”.读作“△ABC全等于△DEF”.
由此,我们可以得出全等三角形的性质:全等三角形的对应边相等,对应角相等。
如图,以直线l为对称轴,画出△ABC的对称图形,并指出它们的对应顶点、对应边和对应角.
若已知∠A=60°,∠B=80°,那么△DEF的各个角的大小:
∠D=60° ,∠E=80°,∠F=40°.
对应边:AB=DE,AC=DF,BC=EF
一标一练
1.(1)若AB=AC,则添加什么条件可得ΔABD≌ΔACD
(2)若∠BAD= ∠CAD,则添加什么条件可使ΔABD≌ΔACD
D
B
C
A
A
B
D
C
如图,已知线段AC、BD相交于点E,AE=DE,BE=CE。
求证:△ABE≌△DCE
四、例题示范 规范步骤
(对顶角相等)
(S.A.S.)
证明:在△ABE和△DCE中,
(已知)
(已知)
五、针对训练 巩固新知
如图A、E、B、D在同一直线上,AB=DE,AC=DF,AC//DF,求证:△ACB≌△DFE。
1、今天我们学习哪种方法可以判定两个三角形全等?
边角边(S.A.S)
2、通过这节课我们知道,当两个三角形有两边和一角对应相等时,三角形一定全等么?
不一定全等.
六、课堂小结 总结得失
3、本节课你掌握了哪些数学思想方法?
分类讨论与数形结合。
七、达标检测 分层落实
2.如图,D、E分别是AB、AC上的点,且AB=AC,AD=AE,求证:∠B=∠C
3、如图在△ABC中,AB=AC,
AD平分∠BAC,求证:(1)BD=CD
(2)AD⊥BC
1、如图,已知AM=CN,AC=BD,添加一
个条件使△ABM≌△CDN,则添加的条件
为
第2题
第3题
第1题
如图:已知AB=AD,AC=AE,∠1=∠2,试说明△ABC≌△ADE
能力提升
Goodbye
13.2.2 全等三角形的判定条件
教学目标
1.理解全等三角形及相关概念,能够从图形中寻找全等三角形,探索并掌握全等三角形的性质,能够利用性质解决简单的问题,以及对两个三角形全等的条件的探索
2.在探索全等三角形性质与三角形全等的条件的过程中,体会研究问题的方法,感受图形变化.
3.培养学生的分类讨论、归纳总结能力和应用意识.培养学生仔细认真的学习态度。
新课引入
1、请同学们观察下面的图形,看你有什么发现没有?
发现这两个图形可以完全重合。
像这样可以互相重合的两个图形,我们把他叫做——全等形。
那么这两个五角星我们就叫做全等五角星。
全等图形既包括规则图形,也包括不规则图形。
2、观察这两个三角形,你有什么发现?
发现他们两个三角形也是完全重合的。
那么这两个三角形我们把他叫做全等三角形。
这就是我们这节课要学习的知识--------------全等三角形.
“全等”用符号“≌”来表示,读作“全等于”,要注意符号的书写规范。
那么怎么用数学语言来表示这两个三角形全等呢?
△ABC ≌ △DEF
这时,点A与点D重合.点B与点E重合.我们把这样互相重合的一对点叫做对应顶点;AB边与DE边重合,这样互相重合的边就叫做对应边;∠A与∠D重合,它们就是对应角.△ABC与△DEF全等,我们把它记作:“△ABC≌△DEF”.读作“△ABC全等于△DEF”.
由此,我们可以得出全等三角形的性质:全等三角形的对应边相等,对应角相等。
如图,以直线l为对称轴,画出△ABC的对称图形,并指出它们的对应顶点、对应边和对应角.
若已知∠A=60°,∠B=80°,那么△DEF的各个角的大小:
∠D=60° ,∠E=80°,∠F=40°.
对应边:AB=DE,AC=DF,BC=EF
一标一练
1.(1)若AB=AC,则添加什么条件可得ΔABD≌ΔACD
(2)若∠BAD= ∠CAD,则添加什么条件可使ΔABD≌ΔACD
D
B
C
A
A
B
D
C
如图,已知线段AC、BD相交于点E,AE=DE,BE=CE。
求证:△ABE≌△DCE
四、例题示范 规范步骤
(对顶角相等)
(S.A.S.)
证明:在△ABE和△DCE中,
(已知)
(已知)
五、针对训练 巩固新知
如图A、E、B、D在同一直线上,AB=DE,AC=DF,AC//DF,求证:△ACB≌△DFE。
1、今天我们学习哪种方法可以判定两个三角形全等?
边角边(S.A.S)
2、通过这节课我们知道,当两个三角形有两边和一角对应相等时,三角形一定全等么?
不一定全等.
六、课堂小结 总结得失
3、本节课你掌握了哪些数学思想方法?
分类讨论与数形结合。
七、达标检测 分层落实
2.如图,D、E分别是AB、AC上的点,且AB=AC,AD=AE,求证:∠B=∠C
3、如图在△ABC中,AB=AC,
AD平分∠BAC,求证:(1)BD=CD
(2)AD⊥BC
1、如图,已知AM=CN,AC=BD,添加一
个条件使△ABM≌△CDN,则添加的条件
为
第2题
第3题
第1题
如图:已知AB=AD,AC=AE,∠1=∠2,试说明△ABC≌△ADE
能力提升
Goodbye
