2022-2023学年华师大版数学八年级上册 13.2.4 角边角 课件(共22张ppt)
文档属性
| 名称 | 2022-2023学年华师大版数学八年级上册 13.2.4 角边角 课件(共22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 251.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-24 15:15:54 | ||
图片预览





文档简介
13.2.4 角边角
教学目标
1.使学生理解A.S.A.与A.A.S.的内容,能运用A.S.A.和A.A.S.证明三角形全等进而说明线段或角相等; 2.使学生体会探索发现问题的过程,经历自己探索出A.A.S.的三角形全等的判定方法及其应用. 3.通过画图、实验、发现、应用的过程教学,树立学生知识于实践用于实践的观念.
教学重难点
重点:理解A.S.A.与A.A.S.定理,并能用它们证明三角形全等. 难点:利用A.S.A.与A.A.S.定理间接说明角相等或线段相等.
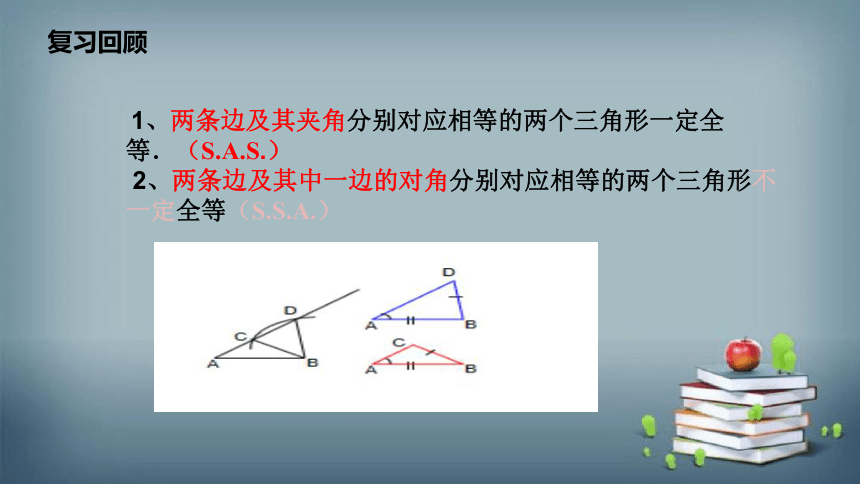
复习回顾
1、两条边及其夹角分别对应相等的两个三角形一定全等.(S.A.S.) 2、两条边及其中一边的对角分别对应相等的两个三角形不一定全等(S.S.A.)
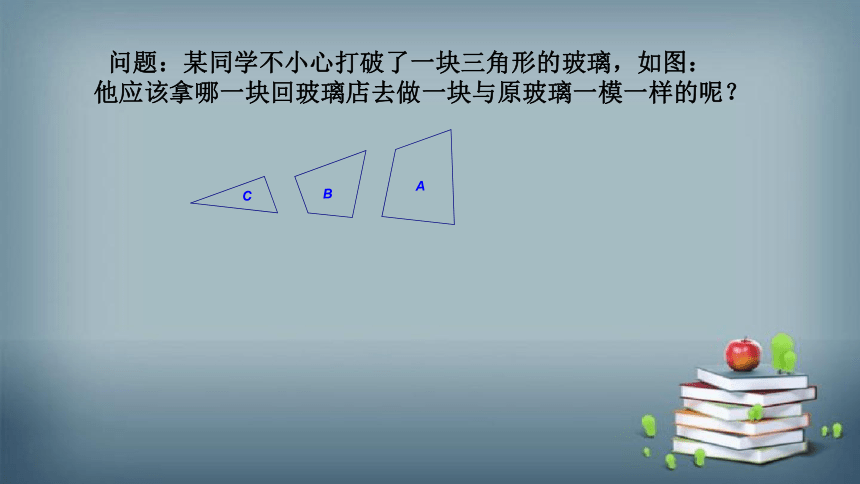
问题:某同学不小心打破了一块三角形的玻璃,如图:他应该拿哪一块回玻璃店去做一块与原玻璃一模一样的呢?
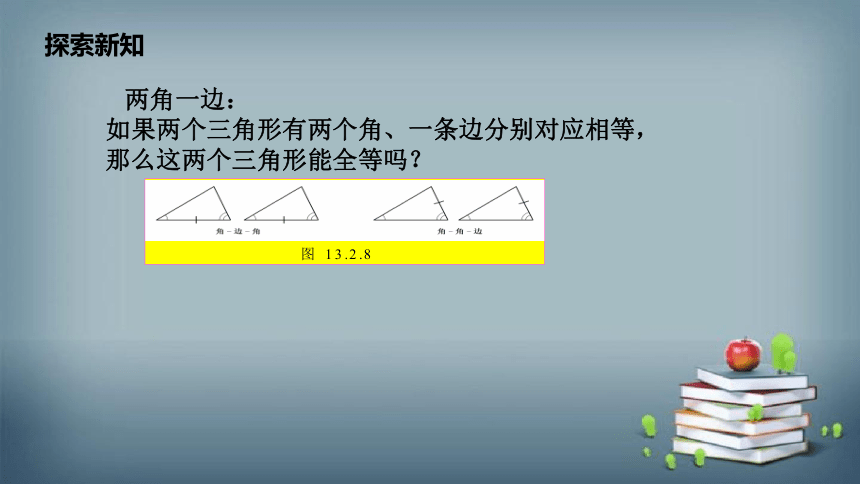
探索新知
两角一边: 如果两个三角形有两个角、一条边分别对应相等,那么这两个三角形能全等吗?
画一画:: 1、动手探究:已知两个角60°,40°和一条线段4cm,以这两个角为内角,以这条线段为两个角的夹边,画一个三角形。把你所画的三角形与其他同学画的进行比较,看一看它们是否都是完全重合的?
画法:
把你所画的三角形与其他同学所画的三角形比较,可以发现什么事实?
做一做:
学生活动:按照下面的步骤画三角形,使它的两个内角分别为60°和 40°,并且这两个角的夹边的长为3cm。
(1)画一条线段AB,使AB=3cm;
(2)画∠MAB=60°,∠NBA= 40°,MA与NB交与点C,△ABC即为所求。
60°
40°
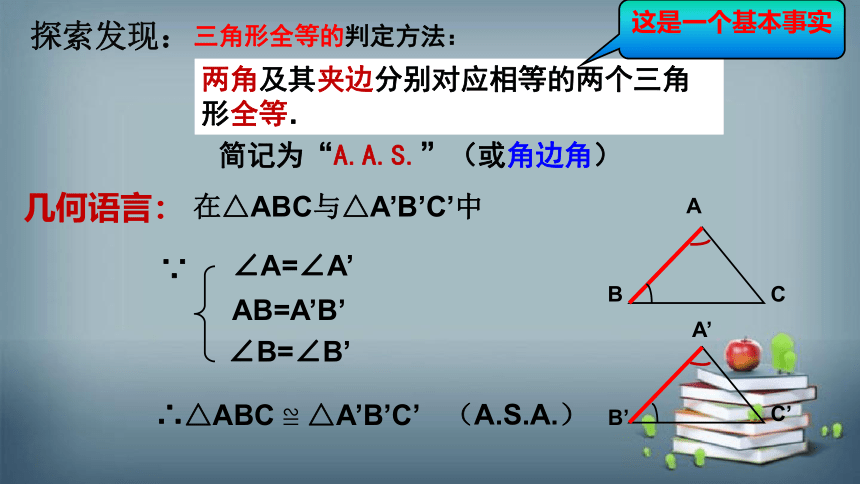
如果两个三角形有两角及其夹边分别对应相等,那么这两个三角形全等.
三角形全等的判定方法:
几何语言:
在△ABC与△A’B’C’中
A
B
C
A’
B’
C’
∵
∴△ABC ≌ △A’B’C’
(A.S.A.)
AB=A’B’
∠B=∠B’
两角及其夹边分别对应相等的两个三角形全等.
简记为“A.A.S.”(或角边角)
探索发现:
这是一个基本事实
∠A=∠A’
例题讲解:
已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C。求证:△ABE≌△ACD
例1.
思考
如下图,在△ABC和△DEF中,∠A =∠D ∠ B=∠E, BC=EF, △ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?
E
F
D
B
A
C
两个角和其中一个角的对边对应相等的两个三角形全等 (简写成“角角边”或“A.A.S.”)
数学符号语言表达:
在ΔABC和ΔDEF中
小结归纳
B
A
C
E
F
D
如果已知两个三角形有两角一边对应相等时,应分为几种情形讨论?
角-边-角
角-角-边
A'
B'
C'
A
B
C
新知引入:
A'
B'
C'
A
B
C
两个三角形全等
两角一边对应相等
例2.已知,如图,∠1=∠2,∠C=∠D.
求证:AC=AD
在△ABD和△ABC中
∠1=∠2 (已知)
∠D=∠C(已知)
AB=AB(公共边)
∴△ABD≌△ABC (A.A.S.)
∴AC=AD (全等三角形对应边相等)
证明:
1
2
例题讲解:
1.如图,应填什么就有 △AOC≌ △BOD
∠A=∠B (已知)
(已知)
∠C=∠D (已知)
∴△AOC≌△BOD(A.S.A.)
课堂训练:
AC=BD
证明:在△ACD和△ABE中,
∠A=∠A(公共角)
AC=AB (已知)
∠C=∠B(已知)
∴ △ACD≌ △ABE(A.S.A.)
∴ AD=AE(全等三角形的性质)
课堂训练:
已知,如图,D在AB上,E在AC上,AB=AC,∠B=∠C,求证:AD=AE
∵
已知:如图,∠1= ∠2, ∠3 = ∠4。
求证: AC=AD。
1
2
3
4
A
B
C
D
课堂训练:
如图,AB⊥BC,AD⊥DC,∠1=∠2,求证:AB=AD
证明:∵AB⊥BC,AD⊥DC(已知)
∴ ∠B=∠D=900
在⊿ABC和⊿ADC中
∠1=∠2
∠B=∠D
AC=AC(公共边)
∴⊿ABC≌⊿ADC(AAS)
∴ AB=AD
拓展训练
已知:AB∥CD,AB=CD,点B、E、F、D在同一直线上,∠A=∠C,求证:AE=CF
证明:∵ AB∥CD (已知)
∴ ∠B=∠D(两直线平行,内错角相等)
在⊿ABE和⊿CDF中
∠B=∠D(已证)
AB=CD(已知)
∠A=∠C (已知)
∴⊿ABE≌⊿CDF(ASA)
∴ AE=CF
拓展训练
如图:已知△ABC≌△A1B1C1,AD、A1D1分别是∠BAC和∠B1 A1 C1的角平分线。求证:AD= A1D1
证明:∵ △ABC≌△A1B1C1
∴AB=A1B1,∠B=∠B1, ∠BAC=∠B1A1C1
(全等三角形的性质)
又∵ AD、A1D1分别是∠BAC和∠B1 A1 C1的角平分线
∴∠BAD=∠B1A1C1
在在⊿BAD和⊿B1A1D1中
∠B=∠B1
AB=A1B1
∠BAD=∠B1A1C1
∴ ⊿BAD≌⊿B1A1D1(ASA)
∴ AD= A1D1
提高训练
知识应用
如图,要测量河两岸相对的两点A,B
的距离,可以在AB的垂线BF上取两点
C,D,使BC=CD,再定出BF的垂线
DE,使A, C,E在一条直线上,这时
测得DE的长就是AB的长。为什么?
A
B
C
D
E
F
(1)学习了ASA和AAS。
(2)由实践证明角边角是真命题。
(3)要根据题意选择适当的方法。
(4)证明线段或角相等,就是证明
它们所在的两个三角形全等。
课堂总结
教学目标
1.使学生理解A.S.A.与A.A.S.的内容,能运用A.S.A.和A.A.S.证明三角形全等进而说明线段或角相等; 2.使学生体会探索发现问题的过程,经历自己探索出A.A.S.的三角形全等的判定方法及其应用. 3.通过画图、实验、发现、应用的过程教学,树立学生知识于实践用于实践的观念.
教学重难点
重点:理解A.S.A.与A.A.S.定理,并能用它们证明三角形全等. 难点:利用A.S.A.与A.A.S.定理间接说明角相等或线段相等.
复习回顾
1、两条边及其夹角分别对应相等的两个三角形一定全等.(S.A.S.) 2、两条边及其中一边的对角分别对应相等的两个三角形不一定全等(S.S.A.)
问题:某同学不小心打破了一块三角形的玻璃,如图:他应该拿哪一块回玻璃店去做一块与原玻璃一模一样的呢?
探索新知
两角一边: 如果两个三角形有两个角、一条边分别对应相等,那么这两个三角形能全等吗?
画一画:: 1、动手探究:已知两个角60°,40°和一条线段4cm,以这两个角为内角,以这条线段为两个角的夹边,画一个三角形。把你所画的三角形与其他同学画的进行比较,看一看它们是否都是完全重合的?
画法:
把你所画的三角形与其他同学所画的三角形比较,可以发现什么事实?
做一做:
学生活动:按照下面的步骤画三角形,使它的两个内角分别为60°和 40°,并且这两个角的夹边的长为3cm。
(1)画一条线段AB,使AB=3cm;
(2)画∠MAB=60°,∠NBA= 40°,MA与NB交与点C,△ABC即为所求。
60°
40°
如果两个三角形有两角及其夹边分别对应相等,那么这两个三角形全等.
三角形全等的判定方法:
几何语言:
在△ABC与△A’B’C’中
A
B
C
A’
B’
C’
∵
∴△ABC ≌ △A’B’C’
(A.S.A.)
AB=A’B’
∠B=∠B’
两角及其夹边分别对应相等的两个三角形全等.
简记为“A.A.S.”(或角边角)
探索发现:
这是一个基本事实
∠A=∠A’
例题讲解:
已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C。求证:△ABE≌△ACD
例1.
思考
如下图,在△ABC和△DEF中,∠A =∠D ∠ B=∠E, BC=EF, △ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?
E
F
D
B
A
C
两个角和其中一个角的对边对应相等的两个三角形全等 (简写成“角角边”或“A.A.S.”)
数学符号语言表达:
在ΔABC和ΔDEF中
小结归纳
B
A
C
E
F
D
如果已知两个三角形有两角一边对应相等时,应分为几种情形讨论?
角-边-角
角-角-边
A'
B'
C'
A
B
C
新知引入:
A'
B'
C'
A
B
C
两个三角形全等
两角一边对应相等
例2.已知,如图,∠1=∠2,∠C=∠D.
求证:AC=AD
在△ABD和△ABC中
∠1=∠2 (已知)
∠D=∠C(已知)
AB=AB(公共边)
∴△ABD≌△ABC (A.A.S.)
∴AC=AD (全等三角形对应边相等)
证明:
1
2
例题讲解:
1.如图,应填什么就有 △AOC≌ △BOD
∠A=∠B (已知)
(已知)
∠C=∠D (已知)
∴△AOC≌△BOD(A.S.A.)
课堂训练:
AC=BD
证明:在△ACD和△ABE中,
∠A=∠A(公共角)
AC=AB (已知)
∠C=∠B(已知)
∴ △ACD≌ △ABE(A.S.A.)
∴ AD=AE(全等三角形的性质)
课堂训练:
已知,如图,D在AB上,E在AC上,AB=AC,∠B=∠C,求证:AD=AE
∵
已知:如图,∠1= ∠2, ∠3 = ∠4。
求证: AC=AD。
1
2
3
4
A
B
C
D
课堂训练:
如图,AB⊥BC,AD⊥DC,∠1=∠2,求证:AB=AD
证明:∵AB⊥BC,AD⊥DC(已知)
∴ ∠B=∠D=900
在⊿ABC和⊿ADC中
∠1=∠2
∠B=∠D
AC=AC(公共边)
∴⊿ABC≌⊿ADC(AAS)
∴ AB=AD
拓展训练
已知:AB∥CD,AB=CD,点B、E、F、D在同一直线上,∠A=∠C,求证:AE=CF
证明:∵ AB∥CD (已知)
∴ ∠B=∠D(两直线平行,内错角相等)
在⊿ABE和⊿CDF中
∠B=∠D(已证)
AB=CD(已知)
∠A=∠C (已知)
∴⊿ABE≌⊿CDF(ASA)
∴ AE=CF
拓展训练
如图:已知△ABC≌△A1B1C1,AD、A1D1分别是∠BAC和∠B1 A1 C1的角平分线。求证:AD= A1D1
证明:∵ △ABC≌△A1B1C1
∴AB=A1B1,∠B=∠B1, ∠BAC=∠B1A1C1
(全等三角形的性质)
又∵ AD、A1D1分别是∠BAC和∠B1 A1 C1的角平分线
∴∠BAD=∠B1A1C1
在在⊿BAD和⊿B1A1D1中
∠B=∠B1
AB=A1B1
∠BAD=∠B1A1C1
∴ ⊿BAD≌⊿B1A1D1(ASA)
∴ AD= A1D1
提高训练
知识应用
如图,要测量河两岸相对的两点A,B
的距离,可以在AB的垂线BF上取两点
C,D,使BC=CD,再定出BF的垂线
DE,使A, C,E在一条直线上,这时
测得DE的长就是AB的长。为什么?
A
B
C
D
E
F
(1)学习了ASA和AAS。
(2)由实践证明角边角是真命题。
(3)要根据题意选择适当的方法。
(4)证明线段或角相等,就是证明
它们所在的两个三角形全等。
课堂总结
