13.2.5 边边边 课件(共21张PPT)
文档属性
| 名称 | 13.2.5 边边边 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 462.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-24 15:04:30 | ||
图片预览







文档简介
(共21张PPT)
13.2.5 边边边
教学目标
1、能自己试验探索出判定三角形全等的SSS判定定理。
2 、会应用判定定理SSS进行简单的推理判定两个三角形全等。
教学重难点
【重点】:探索过程,应用SSS.
【难点】:数学归纳法之猜想验证
1、 全等三角形的定义
2、 全等三角形有什么性质?已知△ABC≌△DEF:
问题1:其中相等的边有:
问题2:其中相等的角有:
问题3:如果两个三角形的三条边对应相等,那么这两个三角形全等吗?
满足下列条件的两个三角形是一定否全等:
3、尺规作图,对比两个三边相等的三角形是否全等
先任意画出一个△ABC,再画一个△ A’B’C’,使
A’B’= AB ,B’C’ =BC,C’ A’= CA,把画好的△ A’B’C’
剪下,放到出的△ABC上,它们全等吗? 全等
到目前为止,我们学习了哪几种判定三角形全等的方法?
1.根据定义;
2.基本事实:S.A.S.,A.S.A.;
3.定理:A.A.S.
如图,已知AD平分∠BAC,要使△ABD≌△ACD,
(1)根据“S.A.S.”需添加条件 ;
(2)根据“A.S.A.”需添加条件 ;
(3)根据“A.A.S.”需添加条件 .
A
B
C
D
AB=AC
∠BDA=∠CDA
∠B=∠C
知识回顾
若两个三角形有三个角对应相等,那么这两个三角形是否全等?
获取新知
画△ABC,其中∠A=50°,∠B=60°, ∠C=70°.
50°
50°
60°
60°
A
B
C
A
B
C
A
B
C
70°
70°
三个角对应相等的两个三角形不一定全等.
可能性1
可能性2
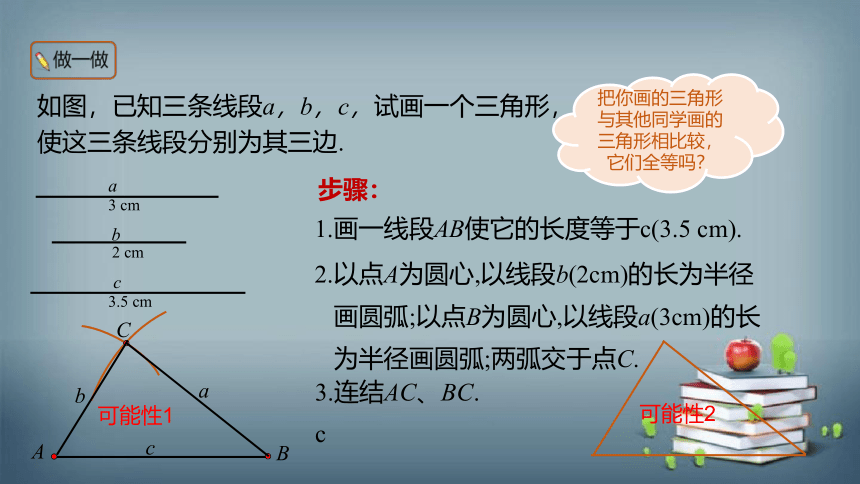
如图,已知三条线段a,b,c,试画一个三角形,使这三条线段分别为其三边.
3 cm
a
2 cm
b
3.5 cm
c
a
b
c
A
B
C
步骤:
1.画一线段AB使它的长度等于c(3.5 cm).
2.以点A为圆心,以线段b(2cm)的长为半径
画圆弧;以点B为圆心,以线段a(3cm)的长
为半径画圆弧;两弧交于点C.
3.连结AC、BC.
c
把你画的三角形与其他同学画的三角形相比较,它们全等吗?
可能性1
可能性2
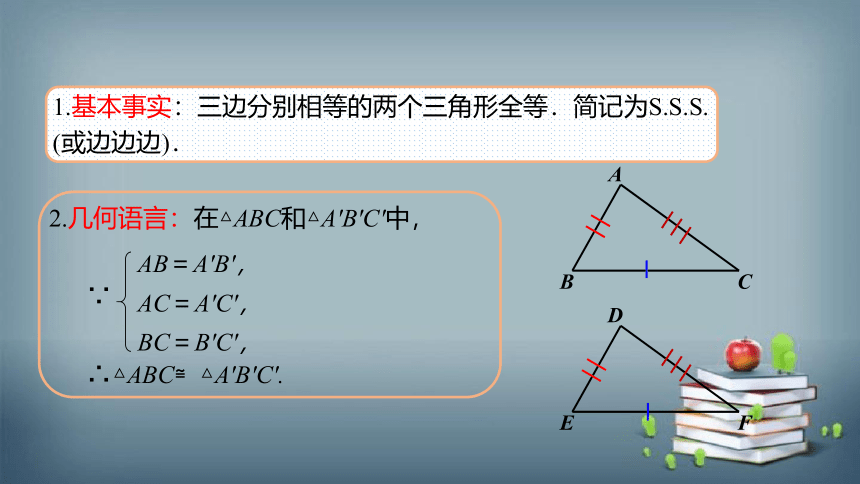
2.几何语言:在△ABC和△A′B′C′中,
∵
∴△ABC≌△A′B′C′.
AB=A′B′,
AC=A′C′,
BC=B′C′,
A
B
C
D
E
F
1.基本事实:三边分别相等的两个三角形全等.简记为S.S.S. (或边边边).
全等三角形的三个基本事实(静态), 其本质与动态的全等三角形定义(轴对称、平移与旋转)是一致的,
例1 如图,有一个三角形钢架,AB =AC ,AD 是连接点A 与BC 中点D 的支架.求证:△ABD ≌△ACD .
解题思路:
先找隐含条件
公共边AD
再找现有条件
AB=AC
最后找准备条件
BD=CD
D是BC的中点
C
B
D
A
例题讲解
证明:∵D 是BC中点,
∴BD =DC.
在△ABD 与△ACD 中,
AB =AC (已知)
BD =CD (已证)
AD =AD (公共边)
指明范围
摆齐根据
写出结论
∴ △ABD ≌ △ACD(S.S.S. ).
准备条件
C
B
D
A
①准备条件:证全等时要用的条件要先证好;
②指明范围:写出在哪两个三角形中;
③摆齐根据:摆出三个条件用大括号括起来;
④写出结论:写出全等结论.
证明的书写步骤:
例2 如图, 在四边形ABCD中,AD= CB,AB= CD.
求证:∠B= ∠D.
证明:在△ABC和△ CDA 中,
∵CB=AD, AB=CD (已知),
AC=CA(公共边),
∴△ ABC≌△ CDA(S.S.S.).
∴ ∠B=∠D(全等三角形的对应角相等).
A
B
C
D
分析:由于∠B 和∠D分别属于△ABC和△ CDA,所以只需证明这两个三角形全等即可
综合法:利用某些已经证明过的结论和性质及已知条件,推导出所要证明的结论成立的方法叫综合法.其思维特点是:由因索果,即从已知条件出发,利用已知的数学定理、性质和公式,推出结论.本书的证明基本上都是用综合法.
本题运用了综合法,根据条件用“S.S.S.”可得到全等的三角形,从全等三角形出发可找到与结论有关的相等的角.
方法指导
关于全等三角形判定的探索得到的结论归纳成下表
对应相等 的元素 两边一角 两角一边 三角
三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中 一角的对边 三角形是否 一定全等 一定 (S. A. S.) 不一定 一定 (A.S. A.) 一定 (A. A.S.) 不一定
一定
(S.S.S)
1. 如图,△ABC中,AB=AC,EB=EC,则由“S.S.S.”可以判定( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上答案都不对
B
随堂演练
2. 如图,已知AC=FE,BC=DE,点A,D,B,F在同一条直线上,要利用“S.S.S.”证明△ABC≌△FDE,还可以添加的一个条件是( )
A.AD=FB B.DE=BD
C.BF=DB D.以上都不对
A
3. 如图,AB=AC,AE=AD,BD=CE,
求证:△AEB ≌△ ADC。
C
A
B
D
E
证明:∵BD=CE
∴ BD-ED=CE-ED,即BE=CD。
在△AEB和△ADC中,
∴ △AEB ≌△ ADC
∵
AB=AC
AE=AD
BE=CD
4.如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?
H
D
C
B
A
解:有三组
在△ABH和△ACH中 ∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);
在△ABH和△ACH中
∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);
在△ABH和△ACH中
∵BD=CD,BH=CH,DH=DH
∴△DBH≌△DCH(SSS)
边边边
内容
有三边对应相等的两个三角形全等(简写成 “SSS”)
应用
思路分析
书写步骤
结合图形找隐含条件和现有条件,证准备条件
注意
四步骤
1. 说明两三角形全等所需的条件应按对应边的顺序书写.
2. 结论中所出现的边必须在所证明的两个三角形中.
课堂小结
13.2.5 边边边
教学目标
1、能自己试验探索出判定三角形全等的SSS判定定理。
2 、会应用判定定理SSS进行简单的推理判定两个三角形全等。
教学重难点
【重点】:探索过程,应用SSS.
【难点】:数学归纳法之猜想验证
1、 全等三角形的定义
2、 全等三角形有什么性质?已知△ABC≌△DEF:
问题1:其中相等的边有:
问题2:其中相等的角有:
问题3:如果两个三角形的三条边对应相等,那么这两个三角形全等吗?
满足下列条件的两个三角形是一定否全等:
3、尺规作图,对比两个三边相等的三角形是否全等
先任意画出一个△ABC,再画一个△ A’B’C’,使
A’B’= AB ,B’C’ =BC,C’ A’= CA,把画好的△ A’B’C’
剪下,放到出的△ABC上,它们全等吗? 全等
到目前为止,我们学习了哪几种判定三角形全等的方法?
1.根据定义;
2.基本事实:S.A.S.,A.S.A.;
3.定理:A.A.S.
如图,已知AD平分∠BAC,要使△ABD≌△ACD,
(1)根据“S.A.S.”需添加条件 ;
(2)根据“A.S.A.”需添加条件 ;
(3)根据“A.A.S.”需添加条件 .
A
B
C
D
AB=AC
∠BDA=∠CDA
∠B=∠C
知识回顾
若两个三角形有三个角对应相等,那么这两个三角形是否全等?
获取新知
画△ABC,其中∠A=50°,∠B=60°, ∠C=70°.
50°
50°
60°
60°
A
B
C
A
B
C
A
B
C
70°
70°
三个角对应相等的两个三角形不一定全等.
可能性1
可能性2
如图,已知三条线段a,b,c,试画一个三角形,使这三条线段分别为其三边.
3 cm
a
2 cm
b
3.5 cm
c
a
b
c
A
B
C
步骤:
1.画一线段AB使它的长度等于c(3.5 cm).
2.以点A为圆心,以线段b(2cm)的长为半径
画圆弧;以点B为圆心,以线段a(3cm)的长
为半径画圆弧;两弧交于点C.
3.连结AC、BC.
c
把你画的三角形与其他同学画的三角形相比较,它们全等吗?
可能性1
可能性2
2.几何语言:在△ABC和△A′B′C′中,
∵
∴△ABC≌△A′B′C′.
AB=A′B′,
AC=A′C′,
BC=B′C′,
A
B
C
D
E
F
1.基本事实:三边分别相等的两个三角形全等.简记为S.S.S. (或边边边).
全等三角形的三个基本事实(静态), 其本质与动态的全等三角形定义(轴对称、平移与旋转)是一致的,
例1 如图,有一个三角形钢架,AB =AC ,AD 是连接点A 与BC 中点D 的支架.求证:△ABD ≌△ACD .
解题思路:
先找隐含条件
公共边AD
再找现有条件
AB=AC
最后找准备条件
BD=CD
D是BC的中点
C
B
D
A
例题讲解
证明:∵D 是BC中点,
∴BD =DC.
在△ABD 与△ACD 中,
AB =AC (已知)
BD =CD (已证)
AD =AD (公共边)
指明范围
摆齐根据
写出结论
∴ △ABD ≌ △ACD(S.S.S. ).
准备条件
C
B
D
A
①准备条件:证全等时要用的条件要先证好;
②指明范围:写出在哪两个三角形中;
③摆齐根据:摆出三个条件用大括号括起来;
④写出结论:写出全等结论.
证明的书写步骤:
例2 如图, 在四边形ABCD中,AD= CB,AB= CD.
求证:∠B= ∠D.
证明:在△ABC和△ CDA 中,
∵CB=AD, AB=CD (已知),
AC=CA(公共边),
∴△ ABC≌△ CDA(S.S.S.).
∴ ∠B=∠D(全等三角形的对应角相等).
A
B
C
D
分析:由于∠B 和∠D分别属于△ABC和△ CDA,所以只需证明这两个三角形全等即可
综合法:利用某些已经证明过的结论和性质及已知条件,推导出所要证明的结论成立的方法叫综合法.其思维特点是:由因索果,即从已知条件出发,利用已知的数学定理、性质和公式,推出结论.本书的证明基本上都是用综合法.
本题运用了综合法,根据条件用“S.S.S.”可得到全等的三角形,从全等三角形出发可找到与结论有关的相等的角.
方法指导
关于全等三角形判定的探索得到的结论归纳成下表
对应相等 的元素 两边一角 两角一边 三角
三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中 一角的对边 三角形是否 一定全等 一定 (S. A. S.) 不一定 一定 (A.S. A.) 一定 (A. A.S.) 不一定
一定
(S.S.S)
1. 如图,△ABC中,AB=AC,EB=EC,则由“S.S.S.”可以判定( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上答案都不对
B
随堂演练
2. 如图,已知AC=FE,BC=DE,点A,D,B,F在同一条直线上,要利用“S.S.S.”证明△ABC≌△FDE,还可以添加的一个条件是( )
A.AD=FB B.DE=BD
C.BF=DB D.以上都不对
A
3. 如图,AB=AC,AE=AD,BD=CE,
求证:△AEB ≌△ ADC。
C
A
B
D
E
证明:∵BD=CE
∴ BD-ED=CE-ED,即BE=CD。
在△AEB和△ADC中,
∴ △AEB ≌△ ADC
∵
AB=AC
AE=AD
BE=CD
4.如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?
H
D
C
B
A
解:有三组
在△ABH和△ACH中 ∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);
在△ABH和△ACH中
∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);
在△ABH和△ACH中
∵BD=CD,BH=CH,DH=DH
∴△DBH≌△DCH(SSS)
边边边
内容
有三边对应相等的两个三角形全等(简写成 “SSS”)
应用
思路分析
书写步骤
结合图形找隐含条件和现有条件,证准备条件
注意
四步骤
1. 说明两三角形全等所需的条件应按对应边的顺序书写.
2. 结论中所出现的边必须在所证明的两个三角形中.
课堂小结
