13.2.5 边边边 同步练习(含解析)
文档属性
| 名称 | 13.2.5 边边边 同步练习(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 417.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-24 00:00:00 | ||
图片预览


文档简介
13.2.5边边边
一、单选题
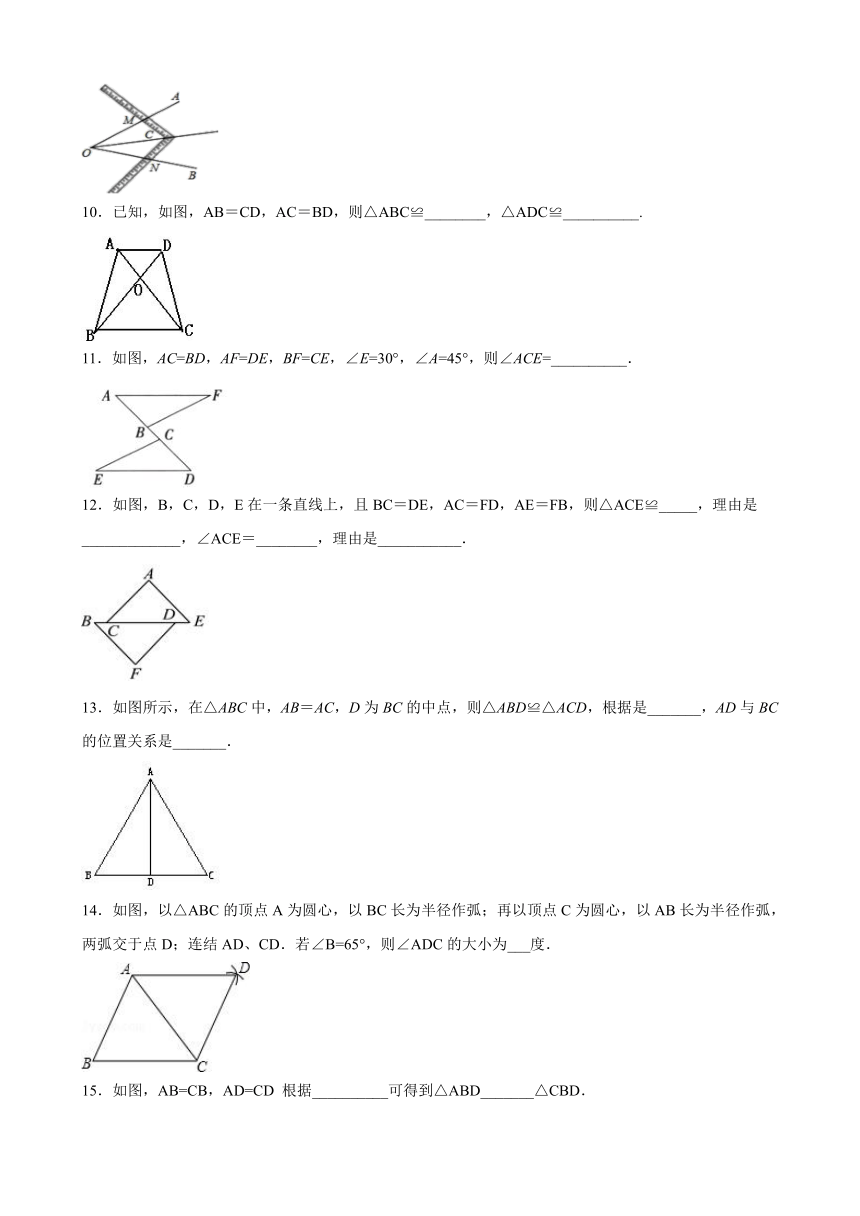
1.如图,交于点O,则下列结论不正确的是( )
A. B. C. D.
2.我国的纸伞工艺十分巧妙.如图,伞不论张开还是缩拢,伞柄始终平分同一平面内两条伞骨所成的角,从而保证伞圈能沿着伞柄滑动.为了证明这个结论,我们的依据是( )
A. B. C. D.
3.如图,在中,,中线和相交于点F,,则图中可用证出的全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
4.如图,由若干个正方形拼成的图形,其中与△ABC全等的三角形是( )
A.△AEG B.△ADF C.△CEG D.△FDG
5.图中的小正方形边长都相等,若,则点Q可能是图中的( )
A.点D B.点C C.点B D.点A
6.如图,在△ABC中,AB=AC,D为BC的中点,则下列结论中:①△ABD≌△ACD;②∠B=∠C;③AD平分∠BAC;④AD⊥BC,其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
7.小明用四根竹棒扎成如图所示的风筝框架,已知AB=CD,AD=CB,下列判断不正确的是( )
A.∠A=∠C B.∠ABC=∠CDA
C.∠ABD=∠CDB D.∠ABC=∠C
8.如图,小明用五根竹棒扎成如图所示的风筝框架,已知AB=CD,AD=CB,下列判断不正确的是( )
A. B. C. D.
二、填空题
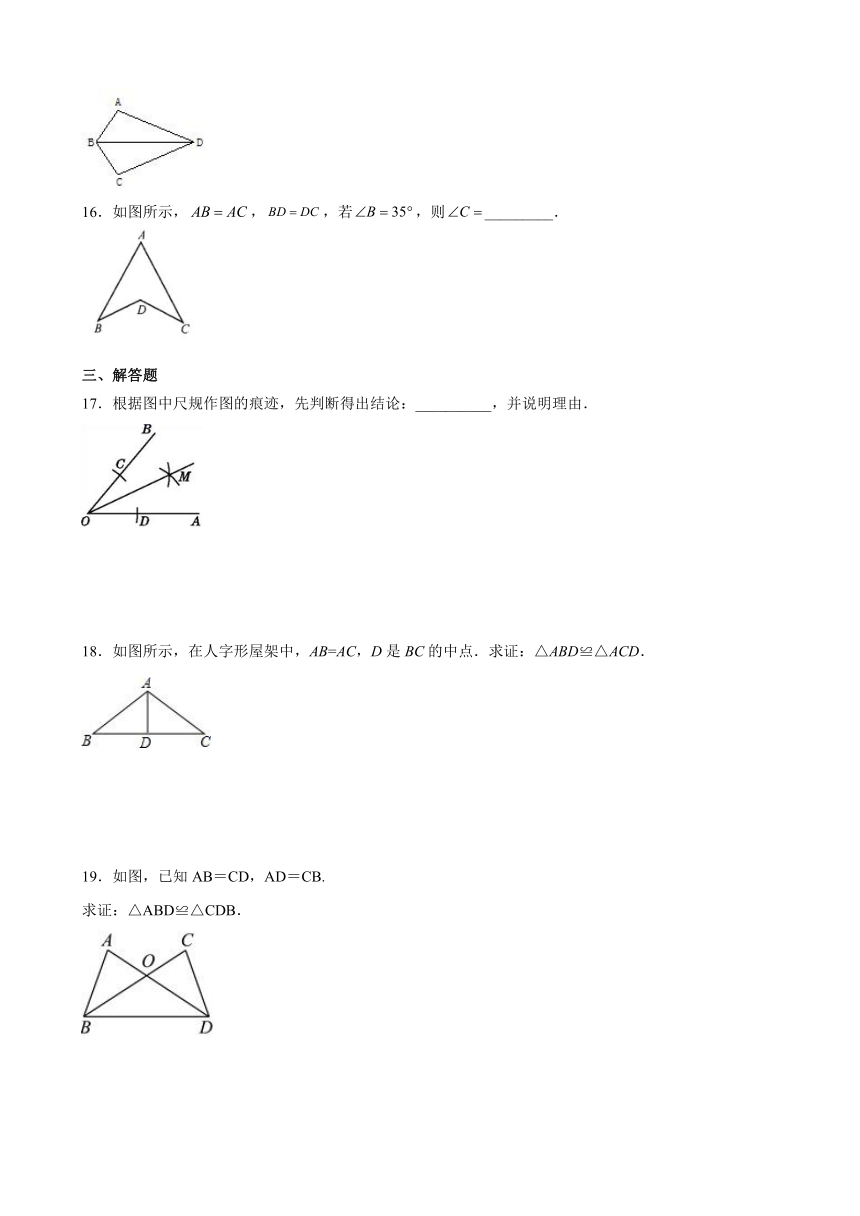
9.工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合.则过角尺顶点C的射线OC便是∠AOB的平分线。这样做的依据是_______.
10.已知,如图,AB=CD,AC=BD,则△ABC≌________,△ADC≌__________.
11.如图,AC=BD,AF=DE,BF=CE,∠E=30°,∠A=45°,则∠ACE=__________.
12.如图,B,C,D,E在一条直线上,且BC=DE,AC=FD,AE=FB,则△ACE≌_____,理由是_____________,∠ACE=________,理由是___________.
13.如图所示,在△ABC中,AB=AC,D为BC的中点,则△ABD≌△ACD,根据是_______,AD与BC的位置关系是_______.
14.如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点D;连结AD、CD.若∠B=65°,则∠ADC的大小为___度.
15.如图,AB=CB,AD=CD 根据__________可得到△ABD_______△CBD.
16.如图所示,,,若,则_________.
三、解答题
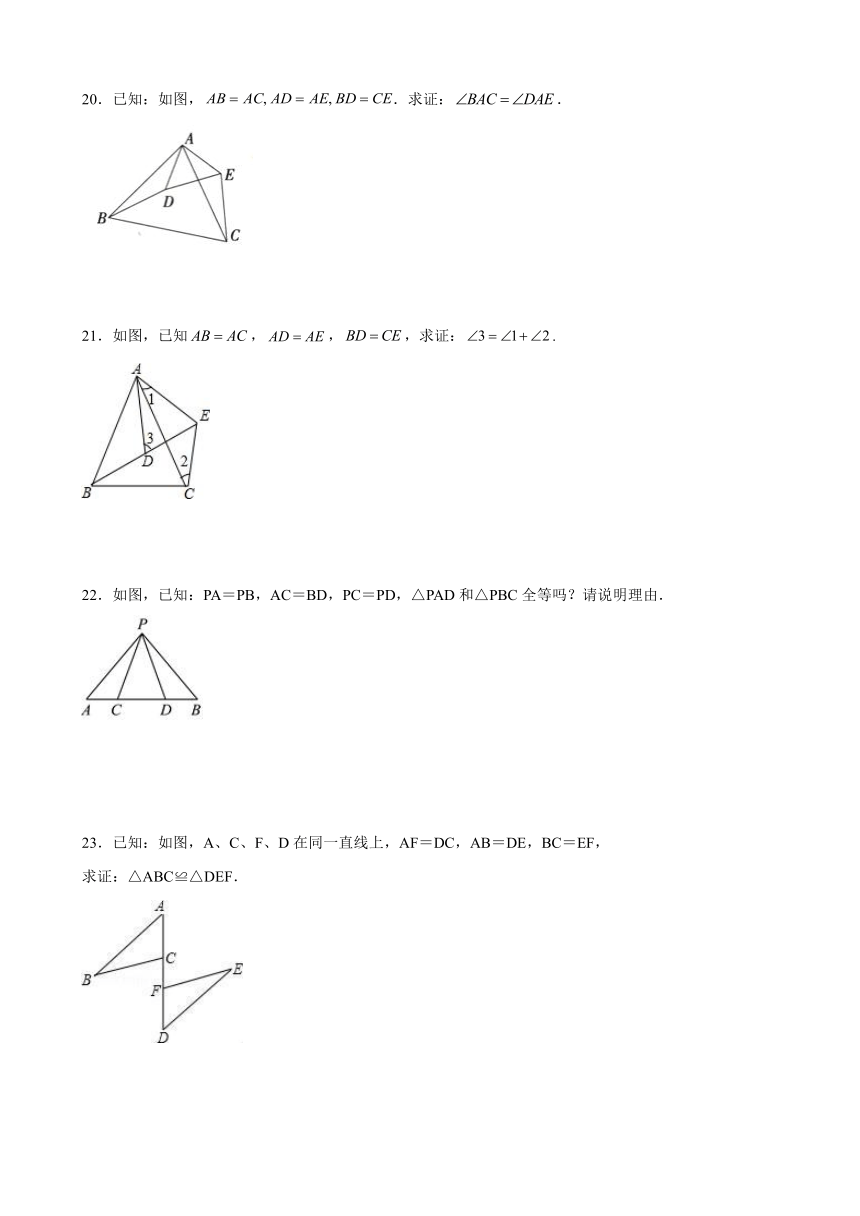
17.根据图中尺规作图的痕迹,先判断得出结论:__________,并说明理由.
18.如图所示,在人字形屋架中,AB=AC,D是BC的中点.求证:△ABD≌△ACD.
19.如图,已知AB=CD,AD=CB.
求证:△ABD≌△CDB.
20.已知:如图,.求证:.
21.如图,已知,,,求证:.
22.如图,已知:PA=PB,AC=BD,PC=PD,△PAD和△PBC全等吗?请说明理由.
23.已知:如图,A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF,
求证:△ABC≌△DEF.
24.如图所示,已知AB=DC,DB=AC.
(1)求证:∠ABD=∠DCA;
(2)在(1)的证明过程中需要作辅助线,它的意图是什么?
参考答案
1.C
【解析】解:A、因为,所以,选项正确;
B、因为,所以正确;
C、由,可以得到,选项错误;
D、由,可得,选项正确.
故选:C
2.A
【解析】根据伞的结构,,伞骨,是公共边,
在和中,
,
,
,
即平分.
故选:.
3.C
【解析】解:∵分别是中线,
∴,
∵,
∴.
在和中,
∵
∴;
在和中,
∵
∴
∴∠DBC=∠ECB,
∴FB=FC,
∴EF=EC-FC=BD-FB=FD,
在和中,
∵
∴≌(SSS)
故可由证出3对全等三角形.
故选择C.
4.D
【解析】解:
在△ABC中,BC=,AC=,AB=3,
在△AEG中,EG=,AG=2,AE=,
在△ADF中,AD=,DF=3,AF=,
在△CEG中,EG=,CG=CE=,
在△FDG中,DG=,FG=,DF=3,
所以BC=DG,AC=FG,AB=DF,
所以△ABC≌△FDG(SSS).
故选D.
5.A
【解析】解:观察图象可知△MNP≌△MFD.
故选:A.
6.D
【解析】∵D为BC的中点,
∴BD=CD,
又∵AB=AC,AD为公共边
∴△ABD≌△ACD(SSS),故①正确,
∴∠B=∠C,∠BAD=∠CAD,∠ADB=∠ADC,
∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,即AD⊥BC,故②③④正确.
综上所述:正确的结论有①②③④共4个,
故选D.
7.D
【解析】∵AB=CD,AD=CB,BD=DB
∴△ABD≌△CDB(SSS),
∴∠A=∠C,∠ABD=∠CDB;故A、C选项正确,
∵∠ABD=∠CDB,∠CBD=∠ADB,
∴∠ABD-∠CBD=∠CDB-∠ADB,即∠ABC=∠CDA,故B选项正确,
∵∠ABC与∠C不是对应角,
∴∠ABC与∠C不相等.故D选项不正确,
故选D.
8.D
【解析】解:∵AB=CD,AD=CB
又BD=DB
∴△ABD≌△CDB
∴∠A=∠C,∠ABD=∠CDB;
又∠ABD=∠CDB,∠CBD=∠ADB
∴∠ABC=∠CDA,
∠ABD与∠C不是对应角不相等.
故选D.
9.SSS证明△COM≌△CON,全等三角形对应角相等
【解析】由图可知,CM=CN,又OM=ON,OC为公共边,
∴△COM≌△CON,
∴∠AOC=∠BOC,
即OC即是∠AOB的平分线.
故答案为:SSS证明△COM≌△CON,全等三角形对应角相等.
10.△DCB, △DAB.
【解析】∵AB=CD,AC=BD,BC=CB,
∴△ABC≌△DCB(SSS),
∵AB=CD,AC=BD,AD=AD,
∴△ADC≌△DAB.
11.
【解析】解:∵AC=BD,
∴AC BC=BD BC,
∴AB=DC,
又∵AF=DE,BF=CE,
∴△ABF≌△DCE(SSS),
∴∠D=∠A=45°,
∴∠ACE=∠D+∠E=45°+30°=75°.
故答案为:75°.
12.△FDB SSS ∠FDB 全等三角形的对应角相等
【解析】∵BC=DE,
∴BC+CD=DE+CD,即BD=CE,
又∵AC=FD,AE=FB,
∴△ACE≌△FDB,(SSS)
∵全等三角形对应角相等,
∴∠ACE=∠FDB,
故答案为△FDB;SSS;∠FDB;全等三角形的对应角相等
13.“边边边公理(SSS)” , AD⊥BC
【解析】∵D为BC的中点
∴BD=CD
又∵AB=AC,AD=AD(公共边)
∴△ABD≌△ACD(SSS)
∴∠ADB=∠ADC=90°
∴AD⊥BC
14.65
【解析】解:∵以点A为圆心,以BC长为半径作弧;以顶点C为圆心,以AB长为半径作弧,两弧交于点D,
∴AB=CD,BC=AD.
又∵AC=CA,∴△ABC≌△CDA(SSS).
∴∠ADC=∠B=65°.
故答案为:65.
15.SSS ≌
【解析】解:在△ABD与△CBD中,
∴△ABD≌△CBD(SSS),
16.
【解析】如图所示:连接AD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴,
又∵,
∴.
故答案为:.
17.OM平分∠BOA,理由见解析
【解析】解:如图所示,连接CM,DM,
由作图的痕迹可知,OC=OD,CM=DM,
又因为OM=OM,
所以△COM≌△DOM,
所以∠COM=∠DOM,
所以OM平分∠BOA,
故答案为:OM平分∠BOA.
18.见解析
【解析】证明:∵D是的中点,
∴,
在和中,
∵,
∴.
19.详见解析
【解析】∵AB=CD,AD=CB,BD=BD,
∴△ABD≌△CDB(SSS)
20.见解析
【解析】证明:在和中,
∴
∴,
∴,
即.
21.证明见解析.
【解析】在△ABD和△ACE中,,
∴△ABD≌△ACE,
∴∠BAD=∠1,∠ABD=∠2,
∵∠3=∠BAD+∠ABD,
∴∠3=∠1+∠2.
22.详见解析
【解析】∵AC=BD,
∴AC+CD=BD+CD,即AD=BC,
又∵PA=PB,PC=PD,
∴△PAD≌△PBC(SSS)
23.证明见解析
【解析】∵AF=DC,
∴AF﹣CF=DC﹣CF,即AC=DF;
在△ABC和△DEF中
∴△ABC≌△DEF(SSS)
24.(1)证明见解析; (2)作辅助线的意图是通过作两个三角形的公共边构造全等三角形.
【解析】(1)如图所示,连结AD,
在△BAD和△CDA中,
∵ ,
∴△BAD≌△CDA(SSS),
∴∠ABD=∠DCA(全等三角形的对应角相等);
(2)作辅助线的意图是通过作两个三角形的公共边构造全等三角形.
一、单选题
1.如图,交于点O,则下列结论不正确的是( )
A. B. C. D.
2.我国的纸伞工艺十分巧妙.如图,伞不论张开还是缩拢,伞柄始终平分同一平面内两条伞骨所成的角,从而保证伞圈能沿着伞柄滑动.为了证明这个结论,我们的依据是( )
A. B. C. D.
3.如图,在中,,中线和相交于点F,,则图中可用证出的全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
4.如图,由若干个正方形拼成的图形,其中与△ABC全等的三角形是( )
A.△AEG B.△ADF C.△CEG D.△FDG
5.图中的小正方形边长都相等,若,则点Q可能是图中的( )
A.点D B.点C C.点B D.点A
6.如图,在△ABC中,AB=AC,D为BC的中点,则下列结论中:①△ABD≌△ACD;②∠B=∠C;③AD平分∠BAC;④AD⊥BC,其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
7.小明用四根竹棒扎成如图所示的风筝框架,已知AB=CD,AD=CB,下列判断不正确的是( )
A.∠A=∠C B.∠ABC=∠CDA
C.∠ABD=∠CDB D.∠ABC=∠C
8.如图,小明用五根竹棒扎成如图所示的风筝框架,已知AB=CD,AD=CB,下列判断不正确的是( )
A. B. C. D.
二、填空题
9.工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合.则过角尺顶点C的射线OC便是∠AOB的平分线。这样做的依据是_______.
10.已知,如图,AB=CD,AC=BD,则△ABC≌________,△ADC≌__________.
11.如图,AC=BD,AF=DE,BF=CE,∠E=30°,∠A=45°,则∠ACE=__________.
12.如图,B,C,D,E在一条直线上,且BC=DE,AC=FD,AE=FB,则△ACE≌_____,理由是_____________,∠ACE=________,理由是___________.
13.如图所示,在△ABC中,AB=AC,D为BC的中点,则△ABD≌△ACD,根据是_______,AD与BC的位置关系是_______.
14.如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点D;连结AD、CD.若∠B=65°,则∠ADC的大小为___度.
15.如图,AB=CB,AD=CD 根据__________可得到△ABD_______△CBD.
16.如图所示,,,若,则_________.
三、解答题
17.根据图中尺规作图的痕迹,先判断得出结论:__________,并说明理由.
18.如图所示,在人字形屋架中,AB=AC,D是BC的中点.求证:△ABD≌△ACD.
19.如图,已知AB=CD,AD=CB.
求证:△ABD≌△CDB.
20.已知:如图,.求证:.
21.如图,已知,,,求证:.
22.如图,已知:PA=PB,AC=BD,PC=PD,△PAD和△PBC全等吗?请说明理由.
23.已知:如图,A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF,
求证:△ABC≌△DEF.
24.如图所示,已知AB=DC,DB=AC.
(1)求证:∠ABD=∠DCA;
(2)在(1)的证明过程中需要作辅助线,它的意图是什么?
参考答案
1.C
【解析】解:A、因为,所以,选项正确;
B、因为,所以正确;
C、由,可以得到,选项错误;
D、由,可得,选项正确.
故选:C
2.A
【解析】根据伞的结构,,伞骨,是公共边,
在和中,
,
,
,
即平分.
故选:.
3.C
【解析】解:∵分别是中线,
∴,
∵,
∴.
在和中,
∵
∴;
在和中,
∵
∴
∴∠DBC=∠ECB,
∴FB=FC,
∴EF=EC-FC=BD-FB=FD,
在和中,
∵
∴≌(SSS)
故可由证出3对全等三角形.
故选择C.
4.D
【解析】解:
在△ABC中,BC=,AC=,AB=3,
在△AEG中,EG=,AG=2,AE=,
在△ADF中,AD=,DF=3,AF=,
在△CEG中,EG=,CG=CE=,
在△FDG中,DG=,FG=,DF=3,
所以BC=DG,AC=FG,AB=DF,
所以△ABC≌△FDG(SSS).
故选D.
5.A
【解析】解:观察图象可知△MNP≌△MFD.
故选:A.
6.D
【解析】∵D为BC的中点,
∴BD=CD,
又∵AB=AC,AD为公共边
∴△ABD≌△ACD(SSS),故①正确,
∴∠B=∠C,∠BAD=∠CAD,∠ADB=∠ADC,
∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,即AD⊥BC,故②③④正确.
综上所述:正确的结论有①②③④共4个,
故选D.
7.D
【解析】∵AB=CD,AD=CB,BD=DB
∴△ABD≌△CDB(SSS),
∴∠A=∠C,∠ABD=∠CDB;故A、C选项正确,
∵∠ABD=∠CDB,∠CBD=∠ADB,
∴∠ABD-∠CBD=∠CDB-∠ADB,即∠ABC=∠CDA,故B选项正确,
∵∠ABC与∠C不是对应角,
∴∠ABC与∠C不相等.故D选项不正确,
故选D.
8.D
【解析】解:∵AB=CD,AD=CB
又BD=DB
∴△ABD≌△CDB
∴∠A=∠C,∠ABD=∠CDB;
又∠ABD=∠CDB,∠CBD=∠ADB
∴∠ABC=∠CDA,
∠ABD与∠C不是对应角不相等.
故选D.
9.SSS证明△COM≌△CON,全等三角形对应角相等
【解析】由图可知,CM=CN,又OM=ON,OC为公共边,
∴△COM≌△CON,
∴∠AOC=∠BOC,
即OC即是∠AOB的平分线.
故答案为:SSS证明△COM≌△CON,全等三角形对应角相等.
10.△DCB, △DAB.
【解析】∵AB=CD,AC=BD,BC=CB,
∴△ABC≌△DCB(SSS),
∵AB=CD,AC=BD,AD=AD,
∴△ADC≌△DAB.
11.
【解析】解:∵AC=BD,
∴AC BC=BD BC,
∴AB=DC,
又∵AF=DE,BF=CE,
∴△ABF≌△DCE(SSS),
∴∠D=∠A=45°,
∴∠ACE=∠D+∠E=45°+30°=75°.
故答案为:75°.
12.△FDB SSS ∠FDB 全等三角形的对应角相等
【解析】∵BC=DE,
∴BC+CD=DE+CD,即BD=CE,
又∵AC=FD,AE=FB,
∴△ACE≌△FDB,(SSS)
∵全等三角形对应角相等,
∴∠ACE=∠FDB,
故答案为△FDB;SSS;∠FDB;全等三角形的对应角相等
13.“边边边公理(SSS)” , AD⊥BC
【解析】∵D为BC的中点
∴BD=CD
又∵AB=AC,AD=AD(公共边)
∴△ABD≌△ACD(SSS)
∴∠ADB=∠ADC=90°
∴AD⊥BC
14.65
【解析】解:∵以点A为圆心,以BC长为半径作弧;以顶点C为圆心,以AB长为半径作弧,两弧交于点D,
∴AB=CD,BC=AD.
又∵AC=CA,∴△ABC≌△CDA(SSS).
∴∠ADC=∠B=65°.
故答案为:65.
15.SSS ≌
【解析】解:在△ABD与△CBD中,
∴△ABD≌△CBD(SSS),
16.
【解析】如图所示:连接AD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴,
又∵,
∴.
故答案为:.
17.OM平分∠BOA,理由见解析
【解析】解:如图所示,连接CM,DM,
由作图的痕迹可知,OC=OD,CM=DM,
又因为OM=OM,
所以△COM≌△DOM,
所以∠COM=∠DOM,
所以OM平分∠BOA,
故答案为:OM平分∠BOA.
18.见解析
【解析】证明:∵D是的中点,
∴,
在和中,
∵,
∴.
19.详见解析
【解析】∵AB=CD,AD=CB,BD=BD,
∴△ABD≌△CDB(SSS)
20.见解析
【解析】证明:在和中,
∴
∴,
∴,
即.
21.证明见解析.
【解析】在△ABD和△ACE中,,
∴△ABD≌△ACE,
∴∠BAD=∠1,∠ABD=∠2,
∵∠3=∠BAD+∠ABD,
∴∠3=∠1+∠2.
22.详见解析
【解析】∵AC=BD,
∴AC+CD=BD+CD,即AD=BC,
又∵PA=PB,PC=PD,
∴△PAD≌△PBC(SSS)
23.证明见解析
【解析】∵AF=DC,
∴AF﹣CF=DC﹣CF,即AC=DF;
在△ABC和△DEF中
∴△ABC≌△DEF(SSS)
24.(1)证明见解析; (2)作辅助线的意图是通过作两个三角形的公共边构造全等三角形.
【解析】(1)如图所示,连结AD,
在△BAD和△CDA中,
∵ ,
∴△BAD≌△CDA(SSS),
∴∠ABD=∠DCA(全等三角形的对应角相等);
(2)作辅助线的意图是通过作两个三角形的公共边构造全等三角形.
