13.2.6 斜边直角边 课件(共20张PPT)
文档属性
| 名称 | 13.2.6 斜边直角边 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 581.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-24 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
13.2.6 斜边直角边
教学目标
1. 探索并掌握两个直角三角形全等的条件:H.L.,并能应用它判别两个直角三角形是否全等;
2. 经历作图、比较、证明等探究过程,提高分析、作图、归纳、表达、逻辑推理等能力;并通过对知识方法的总结,培养反思的习惯,培养理性思维;
3. 经历如何总结出全等三角形识别方法,体会如何探讨、实践、总结,培养学生的合作能力.
教学重难点
直角三角形全等条件的探索过程,培养合情合理的推理能力,能有条理地、清晰地思考并阐述自己的观点,正确灵活运用.
情景导入
舞台背景的形状是两个直角三角形.工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.但工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”,你相信他的结论吗?
新知探究
问题1: 我们知道如果有“边边角”分别对应相等,不能保证这两个三角形全等.那么在两个直角三角形中,当斜边和一条直角边分别对应相等时,也具有“边边角”对应相等的条件,这时这两个直角三角形能否全等呢?
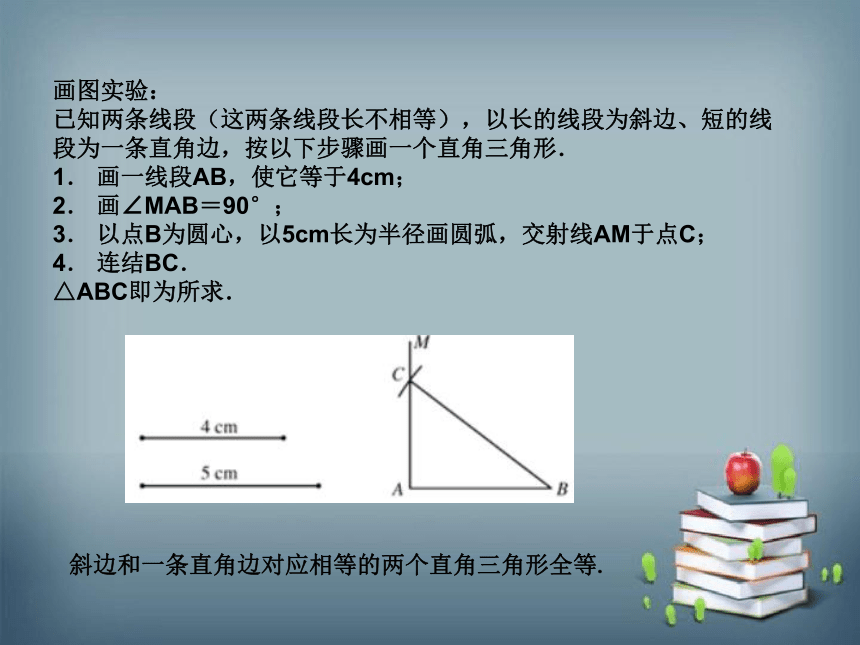
画图实验:
已知两条线段(这两条线段长不相等),以长的线段为斜边、短的线段为一条直角边,按以下步骤画一个直角三角形.
1. 画一线段AB,使它等于4cm;
2. 画∠MAB=90°;
3. 以点B为圆心,以5cm长为半径画圆弧,交射线AM于点C;
4. 连结BC.
△ABC即为所求.
斜边和一条直角边对应相等的两个直角三角形全等.
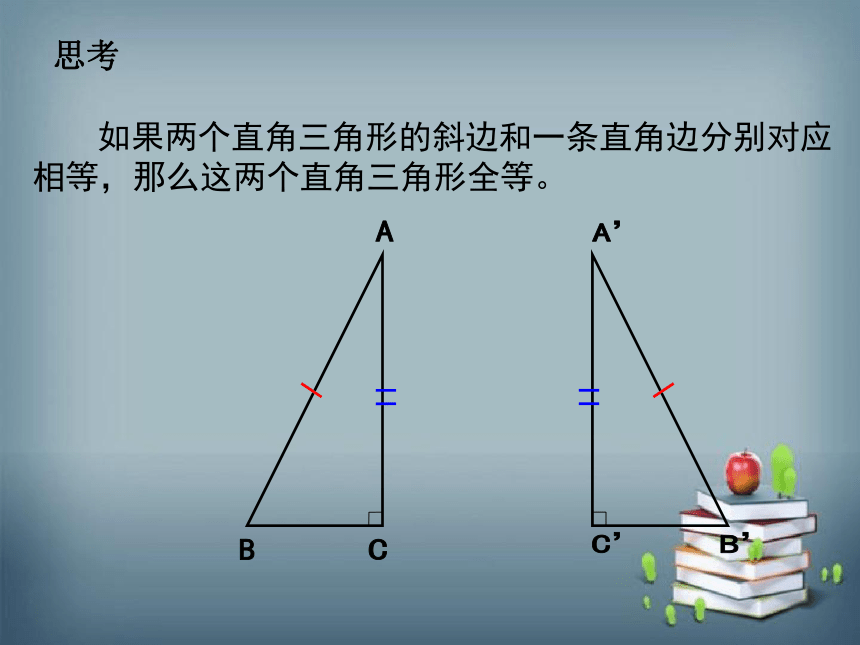
如果两个直角三角形的斜边和一条直角边分别对应
相等,那么这两个直角三角形全等。
思考
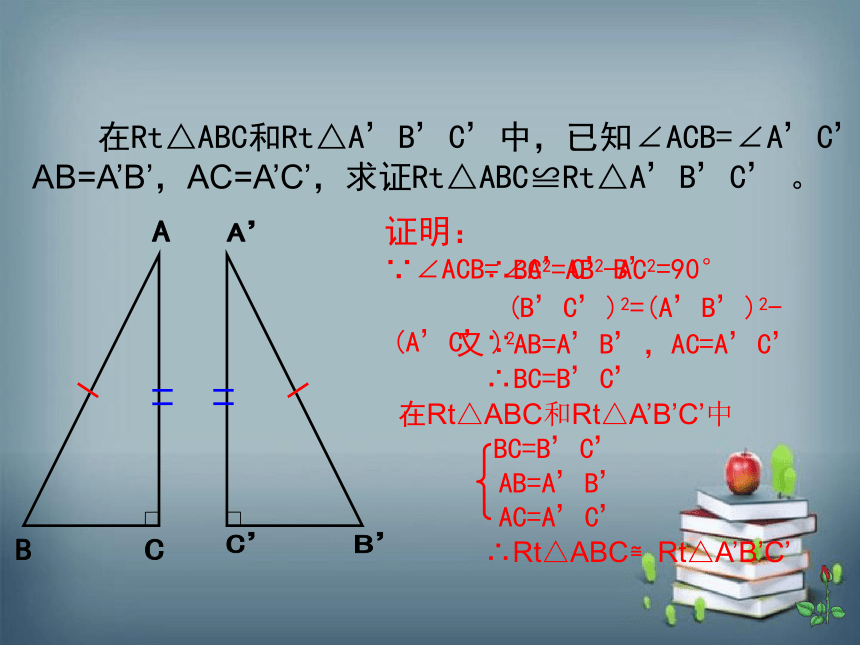
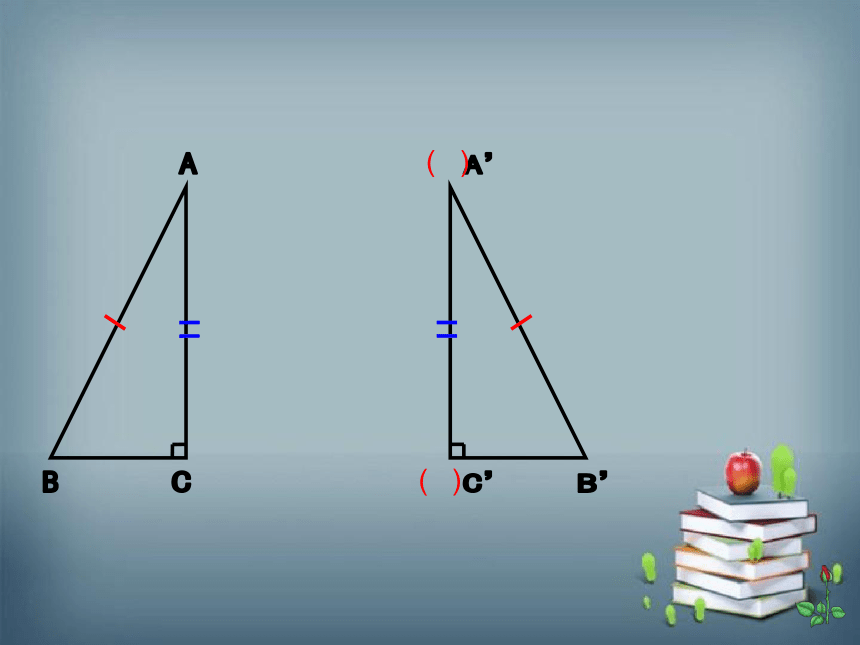
在Rt△ABC和Rt△A’B’C’中,已知∠ACB=∠A’C’B’=90°
AB=A’B’,AC=A’C’,求证Rt△ABC≌Rt△A’B’C’ 。
证明:∵∠ACB=∠A’C’B’=90°
∴BC2=AB2-AC2
(B’C’)2=(A’B’)2-(A’C’)2
又∵AB=A’B’,AC=A’C’
∴BC=B’C’
在Rt△ABC和Rt△A’B’C’中
BC=B’C’
AB=A’B’
AC=A’C’
∴Rt△ABC≌Rt△A’B’C’
( )
( )
斜边直角边定理
如果两个直角三角形的斜边和一条直角边分别对应相等,
那么这两个直角三角形全等。
简记为H.L.
或“斜边直角边”
hypotonuse leg of right triangle
2、判断:甲、乙、丙、丁四个直角三角形中全等的是( )
甲 乙 丙 丁
1、如图:AB⊥CD于O,OA=OB,
添加条件( ),
△AOC≌△BOD
3、如图,AC=AD,∠C=∠D=90°,
BD=3cm,则BC=( )cm
共有几种判断直角三角形全等的方法?
有两条边分别相等的两个直角三角形是否全等?
证明:∵∠C=∠D=90°
∴在Rt△ABC和Rt△BAD中
AC=BD
AB=BA
∴Rt△ABC≌Rt△BAD
(1)求证:AD=BC
(2)求证:∠DBA=∠CAB
例:如图,已知AC=BD,∠C=∠D=90°求证:Rt△ABC≌Rt△BAD。
(3)你还能找到哪些相等的线段和相等的角?
如图,已知AC=BD,∠C=∠D=90°
变式一:作DM⊥AB于M,CN⊥AB于N,DM与CN相等吗?为什么?
如图,已知AC=BD,∠ACB=∠BDA=90°
变式二:求证:AD=BC
如图,已知AC=BD,∠ACB=∠BDA=90°
变式二:求证:AD=BC
春天是放风筝的季节,如图是一个风筝骨
架,为使风筝平衡,须使∠AME=∠BME。
已知:BD⊥AM于D,AC⊥BM于C,AC=BD,
风筝飞行时能平衡吗?为什么?
(不考虑其它原因)
春天是放风筝的季节,如图是一个风筝骨
架,为使风筝平衡,须使∠AME=∠BME。
已知:BD⊥AM于D,AC⊥BM于C,AC=BD,
风筝飞行时能平衡吗?为什么?
(不考虑其它原因)
春天是放风筝的季节,如图是一个风筝骨
架,为使风筝平衡,须使∠AME=∠BME。
已知:BD⊥AM于D,AC⊥BM于C,AC=BD,
风筝飞行时能平衡吗?为什么?
(不考虑其它原因)
答:风筝飞行时能平衡。
证明:∵ BD⊥AM,AC⊥BM,∠MCA=∠MDB=90°
在△MCA和△MBD中
∠MCA=∠MDB
∠AMC=∠BMD
AC=BD
∴△MCA≌△MDB ∴MC=MD
在Rt△MDE和Rt△MCE中
ME=ME
MD=MC
∴Rt△MDE≌Rt△MCE ∴ ∠AME=∠BME
春天是放风筝的季节,如图是一个风筝骨
架,为使风筝平衡,须使∠AME=∠BME。
已知:BD⊥AM于D,AC⊥BM于C,AC=BD,
风筝飞行时能平衡吗?为什么?
(不考虑其它原因)
Rt△ABC≌Rt△BAD
∠CAB=∠DBA
AE=BE
ED=EC
必做题:
1、优化练习册P50 11题、13题、14题
P51 15题、16题
2、数学练习册P34 1题、2题、3题
选做题:
1、优化练习册P52 22题
13.2.6 斜边直角边
教学目标
1. 探索并掌握两个直角三角形全等的条件:H.L.,并能应用它判别两个直角三角形是否全等;
2. 经历作图、比较、证明等探究过程,提高分析、作图、归纳、表达、逻辑推理等能力;并通过对知识方法的总结,培养反思的习惯,培养理性思维;
3. 经历如何总结出全等三角形识别方法,体会如何探讨、实践、总结,培养学生的合作能力.
教学重难点
直角三角形全等条件的探索过程,培养合情合理的推理能力,能有条理地、清晰地思考并阐述自己的观点,正确灵活运用.
情景导入
舞台背景的形状是两个直角三角形.工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.但工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”,你相信他的结论吗?
新知探究
问题1: 我们知道如果有“边边角”分别对应相等,不能保证这两个三角形全等.那么在两个直角三角形中,当斜边和一条直角边分别对应相等时,也具有“边边角”对应相等的条件,这时这两个直角三角形能否全等呢?
画图实验:
已知两条线段(这两条线段长不相等),以长的线段为斜边、短的线段为一条直角边,按以下步骤画一个直角三角形.
1. 画一线段AB,使它等于4cm;
2. 画∠MAB=90°;
3. 以点B为圆心,以5cm长为半径画圆弧,交射线AM于点C;
4. 连结BC.
△ABC即为所求.
斜边和一条直角边对应相等的两个直角三角形全等.
如果两个直角三角形的斜边和一条直角边分别对应
相等,那么这两个直角三角形全等。
思考
在Rt△ABC和Rt△A’B’C’中,已知∠ACB=∠A’C’B’=90°
AB=A’B’,AC=A’C’,求证Rt△ABC≌Rt△A’B’C’ 。
证明:∵∠ACB=∠A’C’B’=90°
∴BC2=AB2-AC2
(B’C’)2=(A’B’)2-(A’C’)2
又∵AB=A’B’,AC=A’C’
∴BC=B’C’
在Rt△ABC和Rt△A’B’C’中
BC=B’C’
AB=A’B’
AC=A’C’
∴Rt△ABC≌Rt△A’B’C’
( )
( )
斜边直角边定理
如果两个直角三角形的斜边和一条直角边分别对应相等,
那么这两个直角三角形全等。
简记为H.L.
或“斜边直角边”
hypotonuse leg of right triangle
2、判断:甲、乙、丙、丁四个直角三角形中全等的是( )
甲 乙 丙 丁
1、如图:AB⊥CD于O,OA=OB,
添加条件( ),
△AOC≌△BOD
3、如图,AC=AD,∠C=∠D=90°,
BD=3cm,则BC=( )cm
共有几种判断直角三角形全等的方法?
有两条边分别相等的两个直角三角形是否全等?
证明:∵∠C=∠D=90°
∴在Rt△ABC和Rt△BAD中
AC=BD
AB=BA
∴Rt△ABC≌Rt△BAD
(1)求证:AD=BC
(2)求证:∠DBA=∠CAB
例:如图,已知AC=BD,∠C=∠D=90°求证:Rt△ABC≌Rt△BAD。
(3)你还能找到哪些相等的线段和相等的角?
如图,已知AC=BD,∠C=∠D=90°
变式一:作DM⊥AB于M,CN⊥AB于N,DM与CN相等吗?为什么?
如图,已知AC=BD,∠ACB=∠BDA=90°
变式二:求证:AD=BC
如图,已知AC=BD,∠ACB=∠BDA=90°
变式二:求证:AD=BC
春天是放风筝的季节,如图是一个风筝骨
架,为使风筝平衡,须使∠AME=∠BME。
已知:BD⊥AM于D,AC⊥BM于C,AC=BD,
风筝飞行时能平衡吗?为什么?
(不考虑其它原因)
春天是放风筝的季节,如图是一个风筝骨
架,为使风筝平衡,须使∠AME=∠BME。
已知:BD⊥AM于D,AC⊥BM于C,AC=BD,
风筝飞行时能平衡吗?为什么?
(不考虑其它原因)
春天是放风筝的季节,如图是一个风筝骨
架,为使风筝平衡,须使∠AME=∠BME。
已知:BD⊥AM于D,AC⊥BM于C,AC=BD,
风筝飞行时能平衡吗?为什么?
(不考虑其它原因)
答:风筝飞行时能平衡。
证明:∵ BD⊥AM,AC⊥BM,∠MCA=∠MDB=90°
在△MCA和△MBD中
∠MCA=∠MDB
∠AMC=∠BMD
AC=BD
∴△MCA≌△MDB ∴MC=MD
在Rt△MDE和Rt△MCE中
ME=ME
MD=MC
∴Rt△MDE≌Rt△MCE ∴ ∠AME=∠BME
春天是放风筝的季节,如图是一个风筝骨
架,为使风筝平衡,须使∠AME=∠BME。
已知:BD⊥AM于D,AC⊥BM于C,AC=BD,
风筝飞行时能平衡吗?为什么?
(不考虑其它原因)
Rt△ABC≌Rt△BAD
∠CAB=∠DBA
AE=BE
ED=EC
必做题:
1、优化练习册P50 11题、13题、14题
P51 15题、16题
2、数学练习册P34 1题、2题、3题
选做题:
1、优化练习册P52 22题
