13.3.2 等腰三角形的判定 学案(无答案)
文档属性
| 名称 | 13.3.2 等腰三角形的判定 学案(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 125.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-24 15:15:32 | ||
图片预览

文档简介
13.3.2 等腰三角形的判定
课标要求 探索并掌握等腰三角形的判定定理;探索等边三角形的判定定理。
学习目标 1.探索并掌握等腰三角形的判定定理,知道等边三角形的判定定理;2.会运用等腰三角形的判定及等边三角形的判定定理进行简单证明
评价任务 1、通过引导探究部分,使学生掌握等腰三角形的判定定理和等边三角形的判定定理(检测目标1)2、通过典例解析、应用练习来落实(检测目标3)
学法建议 1.等腰三角形的判定是华师版八年级上册数学第13章第3节第2课时的内容2.本节内容是在学生已有的平行线性质与判定、命题、全等三角形、等腰三角形的性质等知识基础上进一步研究的问题。特点之一是它揭示了同一个三角形的边、角关系;特点之二是它与等腰三角形的性质定理互为逆定理;特点三是它为我们提供了证明两条线段相等的新方法,为以后的学习提供了证明和计算依据,有助于培养学生思维的灵活性和广阔性。所以本节教材承上又启下、至关重要。3.本节的重点是等腰三角形的判定定理和等边三角形的判定定理①学生通过根据条件(三角形中有两角相等)作图,对比相等两角所对的两边,发现这两边相等的结论;②通过构造全等三角形并利用全等三角形的性质得到两边相等的结论,进一步验证上面的猜想是正确的。③通过例题学习和针对练习达到巩固等腰三角形判定定理的效果,而等边三角形的判定定理则是在等腰三角形的练习中形成的。4、本节课课中学习按以下流程进行:知识预备→引导探究→得出判定定理→典例解析→应用练习→课堂小结→达标检测。5、本节课后达标检测均为合格标准.
【学习过程】
知识预备 1.如图所示,在等腰△ABC中,AB=AC,AD平分∠BAC,(1)若∠1=20°,则∠BAC= ∠B= ∠C= (2)若AB=5,BD=3,则AC、BC的长分别为 。2.画一个等腰三角形
引导探究 1.画一画如图,已知线段BC,∠α;求作△ABC.作法:(1)分别以点B、点C为顶点在线段BC的同侧作角,使∠ABC =∠ACB =∠α,两角的另一边相交于点A;(2)△ABC即为所求. 2.想一想:试动手折一折,说明你的猜想:在△ABC中,线段AB与线段AC有什么关系,以及△ABC的形状。3.说一说通过上面的操作,说说你的发现?将你的发现写出已知求证的形式4.试一试如图,在△ABC中,∠B=∠C.求证:AB=AC 思考:(1)还有其他添加辅助线的方法吗?如果有,试写出证明过程。(2)你能说出等腰三角形的判定定理与性质定理有什么区别与联系吗?
定理归纳 等腰三角形的判定定理
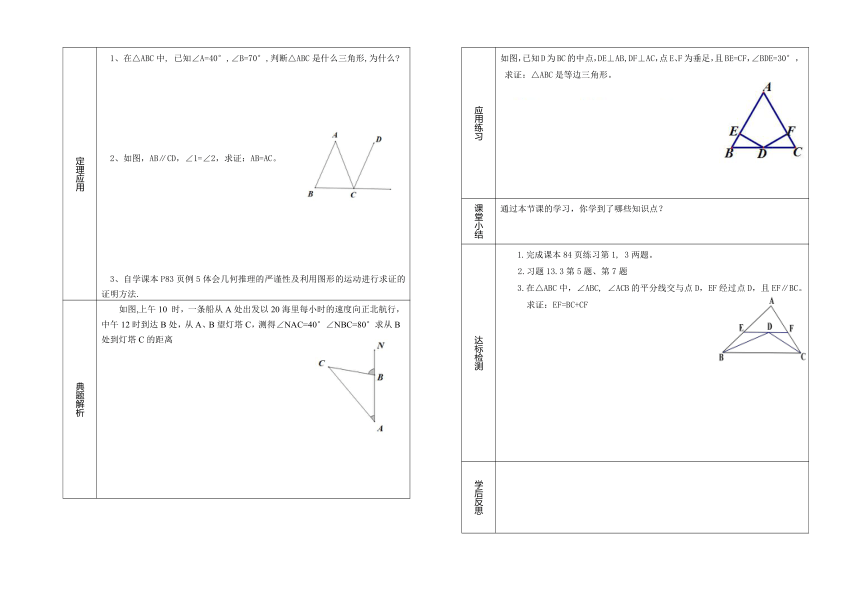
定理应用 在△ABC中, 已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么 2、如图,AB∥CD,∠1=∠2,求证:AB=AC。 3、自学课本P83页例5体会几何推理的严谨性及利用图形的运动进行求证的证明方法.
典题解析 如图,上午10 时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°∠NBC=80°求从B处到灯塔C的距离
应用练习 如图,已知D为BC的中点,DE⊥AB,DF⊥AC,点E、F为垂足,且BE=CF,∠BDE=30°, 求证:△ABC是等边三角形。
课堂小结 通过本节课的学习,你学到了哪些知识点?
达标检测 1.完成课本84页练习第1, 3两题。2.习题13.3第5题、第7题3.在△ABC中,∠ABC, ∠ACB的平分线交与点D,EF经过点D,且EF∥BC。 求证:EF=BC+CF
学后反思
课题:等腰三角形的判定(八年级)
审签:_________ 班级:______ 姓名:_________
基础题知识点1 等角对等边在△ABC中,其两个内角如下,则能判定△ABC为等腰三角形的是( )∠A=40°,∠B=50° B、∠A=40°,∠B=60°∠A=20°,∠B=80° D、∠A=40°,∠B=80°△ABC中,∠A=65°,∠B=50°,则△ABC的形状是 .如图,AC和BD相交于点O,且AB∥DC,OC=OD,求证:△AOB是等腰三角形.4、如图,△ABC中,AB=AC,AD⊥BC,DE∥AC,求证:△BDE和△AED都是等腰三角形.知识点2 等边三角形的判定5、在△ABC中,∠A=60°,AB=AC=3,则△ABC的周长为 .6、如图,在△ABC中,点D是AB上的一点,且AD=DC=DB,∠B=30°,求证:△ADC是等边三角形.7、如图,在△ABC中,AB=AC,∠B=30°,D,E在BC上,且AD=BD,AE=EC。求证:△ADE是等边三角形.中档题8、如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角形的个数为( )A、3个 B 、4个 C、5个 D、6个 9、在△ABC中,BD平分∠ABC,ED∥BC,已知AB=3,AD=1,则△AED的周长为( )A、2 B、3 C、4 D、510、如图,在△ABC中,点D、E分别边AC、AB上,BD与CE交于点O,给出下列三个条件:1.∠EBO=∠DCO;2.BE=CD;3.OB=OC上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形?(用序号写出所有成立的情形)请选择(1)中的一种情形,写出证明过程.11、如图,已知:等边△ABC中,点P,Q,R分别在AB,BC,AC上,且PQ⊥BC于点Q,QR⊥AC于点R,RP⊥AB于点P,求证:△PQR是等边三角形.12、如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,垂足为G,且AD=AB,∠EDF=60°,其两边分别交边AB,AC于点E,F.求证:△ABD是等边三角形BE=AF
14.已知D为△ABC所在平面内一点,且DB=DC,DE⊥AB,DF⊥AC,垂足分别为E,F,DE=DF.(1)如图1,当点D在BC边上时,判断△ABC的形状;并证明你的结论;(2)如图2,当点D在△ABC内部时,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请举出反例(画图说明,不需证明). 综合题15.数学课上,王老师出示了如下框中的题目.如图,在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,试判断线段AE与DB的大小关系,并说明理由.
课标要求 探索并掌握等腰三角形的判定定理;探索等边三角形的判定定理。
学习目标 1.探索并掌握等腰三角形的判定定理,知道等边三角形的判定定理;2.会运用等腰三角形的判定及等边三角形的判定定理进行简单证明
评价任务 1、通过引导探究部分,使学生掌握等腰三角形的判定定理和等边三角形的判定定理(检测目标1)2、通过典例解析、应用练习来落实(检测目标3)
学法建议 1.等腰三角形的判定是华师版八年级上册数学第13章第3节第2课时的内容2.本节内容是在学生已有的平行线性质与判定、命题、全等三角形、等腰三角形的性质等知识基础上进一步研究的问题。特点之一是它揭示了同一个三角形的边、角关系;特点之二是它与等腰三角形的性质定理互为逆定理;特点三是它为我们提供了证明两条线段相等的新方法,为以后的学习提供了证明和计算依据,有助于培养学生思维的灵活性和广阔性。所以本节教材承上又启下、至关重要。3.本节的重点是等腰三角形的判定定理和等边三角形的判定定理①学生通过根据条件(三角形中有两角相等)作图,对比相等两角所对的两边,发现这两边相等的结论;②通过构造全等三角形并利用全等三角形的性质得到两边相等的结论,进一步验证上面的猜想是正确的。③通过例题学习和针对练习达到巩固等腰三角形判定定理的效果,而等边三角形的判定定理则是在等腰三角形的练习中形成的。4、本节课课中学习按以下流程进行:知识预备→引导探究→得出判定定理→典例解析→应用练习→课堂小结→达标检测。5、本节课后达标检测均为合格标准.
【学习过程】
知识预备 1.如图所示,在等腰△ABC中,AB=AC,AD平分∠BAC,(1)若∠1=20°,则∠BAC= ∠B= ∠C= (2)若AB=5,BD=3,则AC、BC的长分别为 。2.画一个等腰三角形
引导探究 1.画一画如图,已知线段BC,∠α;求作△ABC.作法:(1)分别以点B、点C为顶点在线段BC的同侧作角,使∠ABC =∠ACB =∠α,两角的另一边相交于点A;(2)△ABC即为所求. 2.想一想:试动手折一折,说明你的猜想:在△ABC中,线段AB与线段AC有什么关系,以及△ABC的形状。3.说一说通过上面的操作,说说你的发现?将你的发现写出已知求证的形式4.试一试如图,在△ABC中,∠B=∠C.求证:AB=AC 思考:(1)还有其他添加辅助线的方法吗?如果有,试写出证明过程。(2)你能说出等腰三角形的判定定理与性质定理有什么区别与联系吗?
定理归纳 等腰三角形的判定定理
定理应用 在△ABC中, 已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么 2、如图,AB∥CD,∠1=∠2,求证:AB=AC。 3、自学课本P83页例5体会几何推理的严谨性及利用图形的运动进行求证的证明方法.
典题解析 如图,上午10 时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测得∠NAC=40°∠NBC=80°求从B处到灯塔C的距离
应用练习 如图,已知D为BC的中点,DE⊥AB,DF⊥AC,点E、F为垂足,且BE=CF,∠BDE=30°, 求证:△ABC是等边三角形。
课堂小结 通过本节课的学习,你学到了哪些知识点?
达标检测 1.完成课本84页练习第1, 3两题。2.习题13.3第5题、第7题3.在△ABC中,∠ABC, ∠ACB的平分线交与点D,EF经过点D,且EF∥BC。 求证:EF=BC+CF
学后反思
课题:等腰三角形的判定(八年级)
审签:_________ 班级:______ 姓名:_________
基础题知识点1 等角对等边在△ABC中,其两个内角如下,则能判定△ABC为等腰三角形的是( )∠A=40°,∠B=50° B、∠A=40°,∠B=60°∠A=20°,∠B=80° D、∠A=40°,∠B=80°△ABC中,∠A=65°,∠B=50°,则△ABC的形状是 .如图,AC和BD相交于点O,且AB∥DC,OC=OD,求证:△AOB是等腰三角形.4、如图,△ABC中,AB=AC,AD⊥BC,DE∥AC,求证:△BDE和△AED都是等腰三角形.知识点2 等边三角形的判定5、在△ABC中,∠A=60°,AB=AC=3,则△ABC的周长为 .6、如图,在△ABC中,点D是AB上的一点,且AD=DC=DB,∠B=30°,求证:△ADC是等边三角形.7、如图,在△ABC中,AB=AC,∠B=30°,D,E在BC上,且AD=BD,AE=EC。求证:△ADE是等边三角形.中档题8、如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角形的个数为( )A、3个 B 、4个 C、5个 D、6个 9、在△ABC中,BD平分∠ABC,ED∥BC,已知AB=3,AD=1,则△AED的周长为( )A、2 B、3 C、4 D、510、如图,在△ABC中,点D、E分别边AC、AB上,BD与CE交于点O,给出下列三个条件:1.∠EBO=∠DCO;2.BE=CD;3.OB=OC上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形?(用序号写出所有成立的情形)请选择(1)中的一种情形,写出证明过程.11、如图,已知:等边△ABC中,点P,Q,R分别在AB,BC,AC上,且PQ⊥BC于点Q,QR⊥AC于点R,RP⊥AB于点P,求证:△PQR是等边三角形.12、如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,垂足为G,且AD=AB,∠EDF=60°,其两边分别交边AB,AC于点E,F.求证:△ABD是等边三角形BE=AF
14.已知D为△ABC所在平面内一点,且DB=DC,DE⊥AB,DF⊥AC,垂足分别为E,F,DE=DF.(1)如图1,当点D在BC边上时,判断△ABC的形状;并证明你的结论;(2)如图2,当点D在△ABC内部时,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请举出反例(画图说明,不需证明). 综合题15.数学课上,王老师出示了如下框中的题目.如图,在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,试判断线段AE与DB的大小关系,并说明理由.
