人教版数学七年级上册4.3.2 角的比较与运算 课件(共22张PPT)
文档属性
| 名称 | 人教版数学七年级上册4.3.2 角的比较与运算 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 261.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 10:29:53 | ||
图片预览




文档简介
(共22张PPT)
锐角β的范围为:____________.
钝角α的范围为:______________,
锐角<直角<钝角
直角的度数为____,
课前提问:(1分钟)
90°< α<180°
90°
0°<β<90°
它们的大小关系为:
___________________________.
第四章:几何图形初步
4.3.2 角的比较与运算
人教版七年级数学上册
议课小组:七年级数学组
议课时间:2022.10.23
授课时间:2022.11.
学习目标(1分钟)
1、会用不同的方法比较角的大小;(重点)
2、理解角平分线的定义,掌握角平分线几何语言的书写。(难点)
中考考点:比较角的大小,角平分线的定义
自学指导1(1分钟)
仔细阅读课本P134—P135的内容,思考下列问题:
1、我们可以运用什么办法来比较角的大小?
学生自学,教师巡视(3分钟)
另一种方法是将两个角的_____及_______重合,另一条边放在_____________就可以比较大小。
一种方法是_____________________,再进行比较。
顶点
用量角器量出它们的度数
一条边
重合边的同侧
(度量法)
(叠合法)
2、完成P134思考
3、完成P135探究
5、作角平分线的方法 , 。
4、从一个角的 出发,把这个角分成 的两个角的射线,叫做这个角的 。
顶点
相等
平分线
度量法
折纸法
D
O
B
C
A
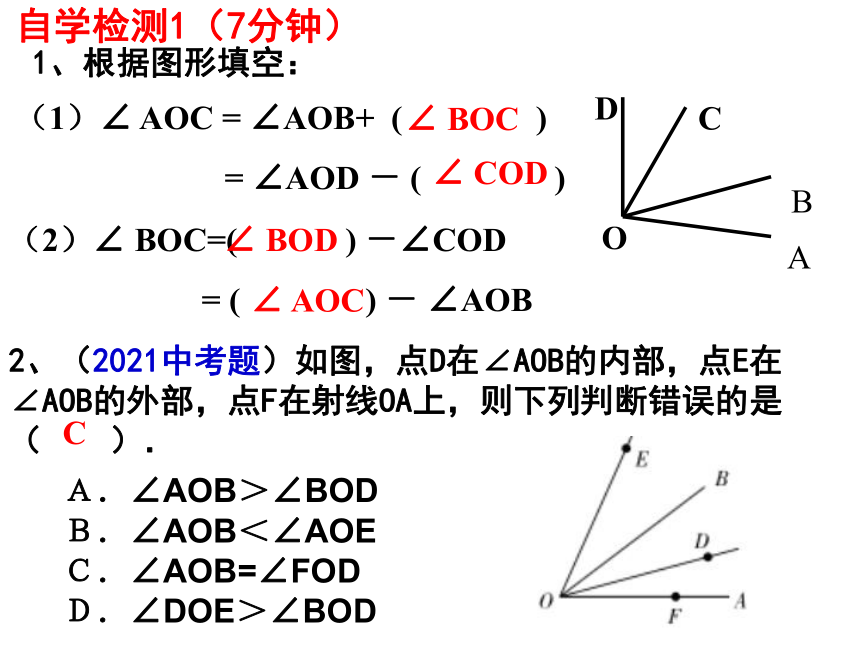
1、根据图形填空:
(1)∠ AOC = ∠AOB+ ( )
= ∠AOD - ( )
(2)∠ BOC=( ) -∠COD
= ( ) - ∠AOB
∠ BOC
∠ COD
∠ BOD
∠ AOC
2、(2021中考题)如图,点D在∠AOB的内部,点E在∠AOB的外部,点F在射线OA上,则下列判断错误的是
( ).
A.∠AOB>∠BOD B.∠AOB<∠AOE
C.∠AOB=∠FOD D.∠DOE>∠BOD
C
自学检测1(7分钟)
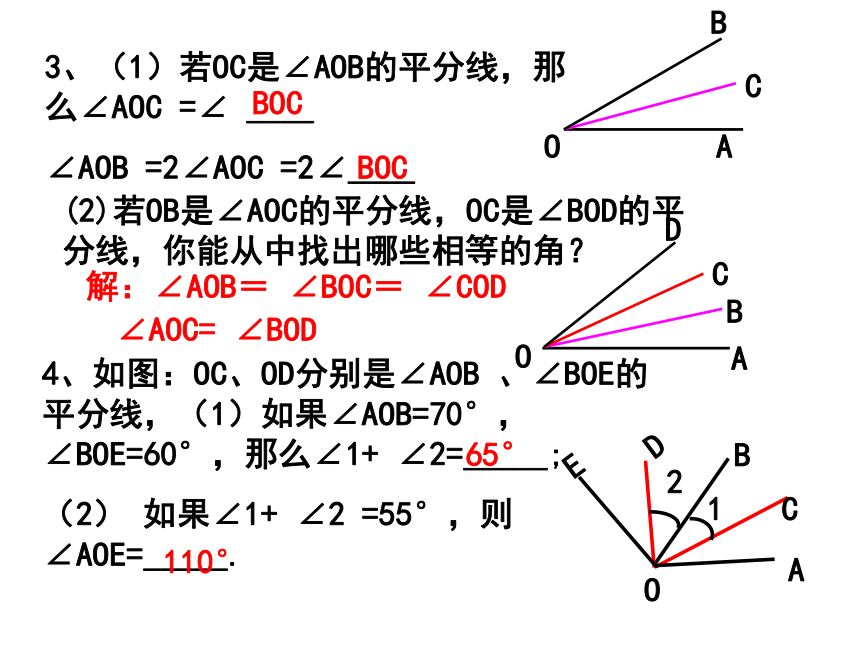
4、如图:OC、OD分别是∠AOB 、∠BOE的平分线,(1)如果∠AOB=70°, ∠BOE=60°,那么∠1+ ∠2=_____;
(2) 如果∠1+ ∠2 =55°,则∠AOE=_____.
65°
110°
A
O
B
C
E
D
1
2
3、(1)若OC是∠AOB的平分线,那么∠AOC =∠ __
∠AOB =2∠AOC =2∠__
O
A
C
B
(2)若OB是∠AOC的平分线,OC是∠BOD的平分线,你能从中找出哪些相等的角?
O
A
B
C
D
解:∠AOB= ∠BOC= ∠COD
∠AOC= ∠BOD
BOC
BOC
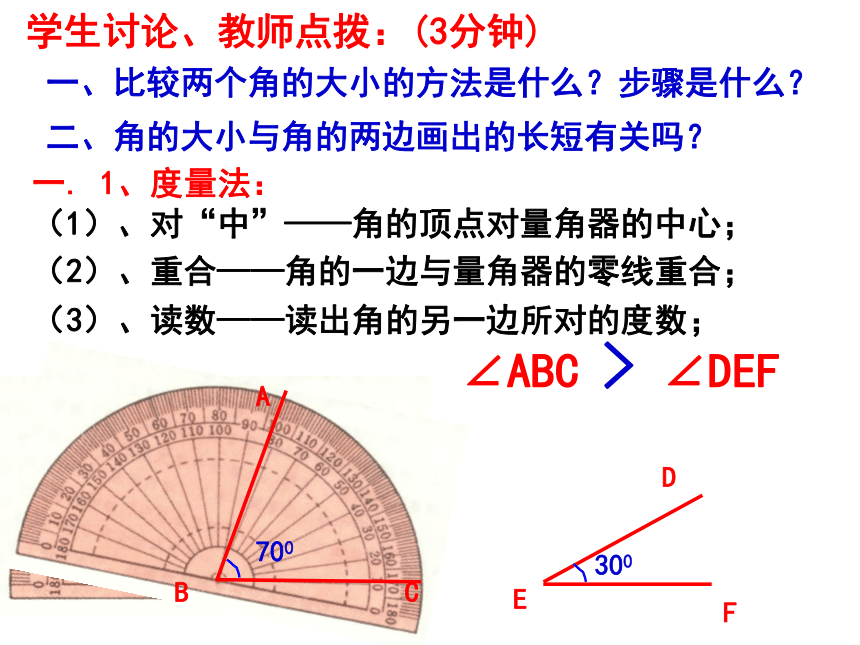
一. 1、度量法:
(1)、对“中”——角的顶点对量角器的中心;
(3)、读数——读出角的另一边所对的度数;
(2)、重合——角的一边与量角器的零线重合;
B
C
A
F
E
D
700
300
∠ABC > ∠DEF
一、比较两个角的大小的方法是什么?步骤是什么?
学生讨论、教师点拨:(3分钟)
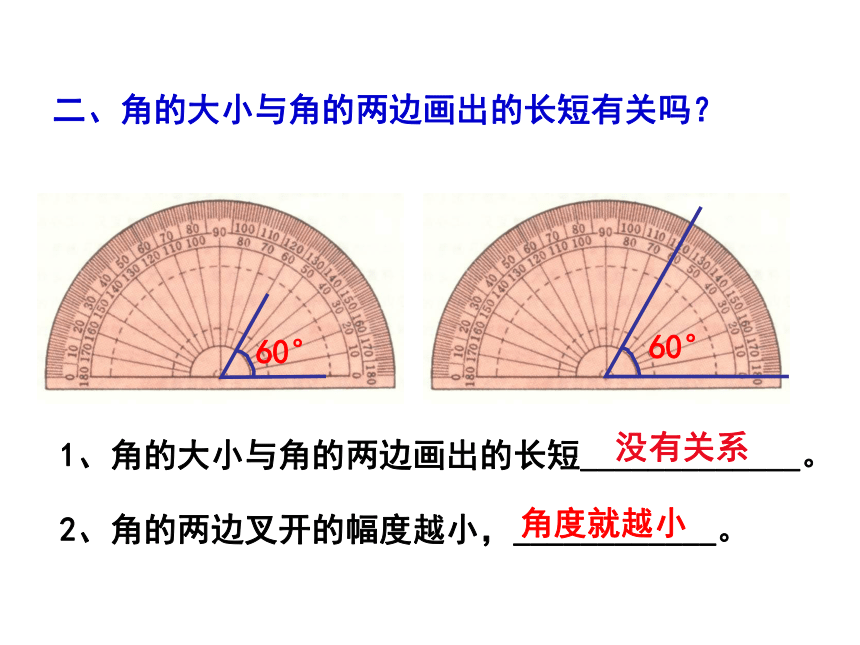
二、角的大小与角的两边画出的长短有关吗?
B
A
O
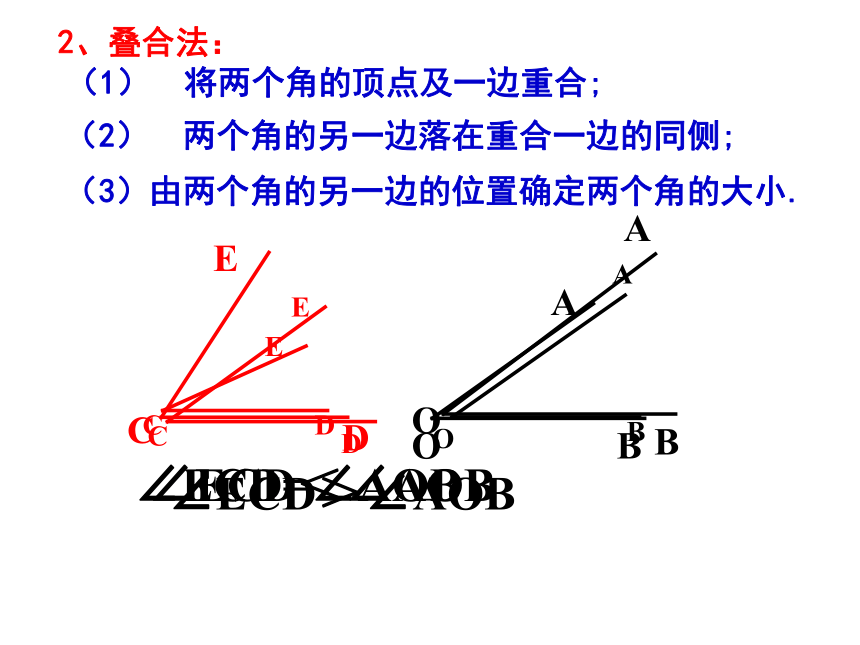
(1) 将两个角的顶点及一边重合;
(2) 两个角的另一边落在重合一边的同侧;
(3)由两个角的另一边的位置确定两个角的大小.
2、叠合法:
C
D
E
∠ECD>∠AOB
O
A
B
D
C
E
∠ECD<∠AOB
A
O
B
C
D
E
∠ECD=∠AOB
二、角的大小与角的两边画出的长短有关吗?
1、角的大小与角的两边画出的长短_____________。
2、角的两边叉开的幅度越小,____________。
60°
60°
没有关系
角度就越小
自学指导2(1分钟)
认真阅读课本P136的内容,理解解题格式和方法。
学生自学,教师巡视(3分钟)
例1 如图,O是直线AB上一点,∠AOC=53 17′,求∠BOC的度数.
解:由题意可知,∠AOB是平角,
∠AOB=∠AOC+∠BOC,
所以∠BOC= ∠AOB-∠AOC
=180 - 53 17′
=126 43′
例2 把一个周角7等分,每一份是多少度的角 (精确到分)
解:360°÷7=51°+3°÷7
=51°+180′÷7
≈51°26′
所以,每份是51°26′
(P136T3)如图,O是直线AB上一点, OC是∠AOB的平分线, ∠COD=31 28′,求∠AOD的度数.
解:由题意可知,∠AOB是平角,
∵OC平分∠AOB
∴∠AOC= ∠AOB
= ×180°
= 90
∴∠AOD=∠AOC-∠COD
=90 -31 28′
=58 32′
自学检测2(7分钟)
∠ = 。
①两个锐角之和一定大于90°;
②两个钝角之和不一定大于180°;
③所有的直角都相等 ;
④ 平角大于 周角
当堂训练(15分钟)
1、下列说法中不正确的是_________.
①②④
2、
BE是 ABC的平分线
ABE
30°
A
B
C
D
E
60°
∠ABC=____+_____=
ABE
CBE
60°
3.(2021中考题)如图,∠AOB=20°,∠BOC=80°,OE是∠AOC的角平分线,则∠COE的度数为
( )
A.50° B.40° C.30° D.20°
A
4、(P140T9)如图,OB是∠AOC平分线,OD平分∠COE,
(1)如果∠AOB=40°,∠DOE=30°
那么∠AOE是多少度?
O
C
A
E
B
D
(变式)已知,如图,∠AOB=130°∠AOD=30°∠BOC=70°,
问:(1)OC是∠AOB的平分线吗?为什么?
(2)OD是∠AOC的平分线吗?为什么?
O
A
D
C
B
4、如图,OB是∠AOC平分线,OD平分∠COE,
(1)如果∠AOB=40°,∠DOE=30°
那么∠AOE是多少度?
O
C
A
E
B
D
∵OB是∠AOC平分线,∠AOB=40°
∴∠BOC=∠AOB=40°
∵OD平分∠COE,∠DOE=30°
∴∠DOC=∠DOE=30°
∴∠BOD=∠BOC+∠DOC=40°+30°=70°
5、已知,如图,∠AOB=130°∠AOD=30°∠BOC=70°,
问:(1)OC是∠AOB的平分线吗?为什么?
(2)OD是∠AOC的平分线吗?为什么?
O
A
D
C
B
解:(1)不是。理由如下:
∵∠AOB=130°,∠BOC=70°
∴∠AOC=∠AOB-∠BOC
=130°-70°=60°≠∠BOC
∴ OC不是∠AOB的平分线。
(2)是。理由如下:
∵∠AOB=130°,∠BOC=70°,∠AOD=30°
∴∠COD=∠AOB-∠BOC-∠AOD
=130°-70°-30°
=30°
∴∠COD=∠AOD,所以OD是∠AOC的平分线。
(选做题)、如图所示,将一张长方形纸斜折过去,使顶点A落在A’处,BC为折痕,然后把BE折过去,使之与A’B重合,折痕为BD那么两折痕BC、BD间的夹角是多少度?
A
A’
B
C
E
D
E’
解:∵ ∠CBA与∠CBA’折叠重合
∴ ∠CBA=∠CBA’
∵ ∠EBD与∠E’BD折叠重合
∴ ∠EBD= ∠ E’BD
∵ ∠CBA+∠CBA’+ ∠EBD+ ∠ E’BD=180°
∴ ∠CBA’+ ∠ E’BD= ×180°=90°
∴ ∠CBD = ∠CBA’+ ∠ E’BD =90°
正本作业 P136 练习 T3
板书设计
1、如何比较两个角的大小:
(1). 度量法
(2). 叠合法
2、角的平分线:
∵
一条射线把一个角分成两个相等的角,则这条射线叫这个角的角平分线。
符号语言
O
A
C
B
思考:下图中共有几个角?
它们有什么关系?
完成下列问题:
1、图中共有__个角,它们分别是______________
2、∠AOB=____+_____
3、∠AOC=____-_____
4、∠BOC=____-_____
3
∠AOB ∠AOC ∠BOC
∠AOC ∠BOC
∠AOB ∠BOC
∠AOB ∠AOC
利用一副三角板,你能画出哪些度数的角?这些角有什么规律?
α
α
α
角的三等分线
α
α
α
α
角的四等分线
⌒
⌒
2
1
O
A
C
B
几何语言
∵∠1=∠2
∴ OC平分∠AOB
一条射线把一个角分成两个相等的角,则这条射线叫这个角的角平分线。
角平分线
角平分线的性质
几何语言
∵OC平分∠AOB
∴∠1=∠2
(或∠AOB= 2∠1 =2∠2)
正本答案
∵∠AOB=180°,
0C是∠AOB的平分线,
∴∠AOC=∠BOC= ∠AOB=90°
∴∠AOD=∠AOC-∠COD
=90°-31°28′
=58°32′
锐角β的范围为:____________.
钝角α的范围为:______________,
锐角<直角<钝角
直角的度数为____,
课前提问:(1分钟)
90°< α<180°
90°
0°<β<90°
它们的大小关系为:
___________________________.
第四章:几何图形初步
4.3.2 角的比较与运算
人教版七年级数学上册
议课小组:七年级数学组
议课时间:2022.10.23
授课时间:2022.11.
学习目标(1分钟)
1、会用不同的方法比较角的大小;(重点)
2、理解角平分线的定义,掌握角平分线几何语言的书写。(难点)
中考考点:比较角的大小,角平分线的定义
自学指导1(1分钟)
仔细阅读课本P134—P135的内容,思考下列问题:
1、我们可以运用什么办法来比较角的大小?
学生自学,教师巡视(3分钟)
另一种方法是将两个角的_____及_______重合,另一条边放在_____________就可以比较大小。
一种方法是_____________________,再进行比较。
顶点
用量角器量出它们的度数
一条边
重合边的同侧
(度量法)
(叠合法)
2、完成P134思考
3、完成P135探究
5、作角平分线的方法 , 。
4、从一个角的 出发,把这个角分成 的两个角的射线,叫做这个角的 。
顶点
相等
平分线
度量法
折纸法
D
O
B
C
A
1、根据图形填空:
(1)∠ AOC = ∠AOB+ ( )
= ∠AOD - ( )
(2)∠ BOC=( ) -∠COD
= ( ) - ∠AOB
∠ BOC
∠ COD
∠ BOD
∠ AOC
2、(2021中考题)如图,点D在∠AOB的内部,点E在∠AOB的外部,点F在射线OA上,则下列判断错误的是
( ).
A.∠AOB>∠BOD B.∠AOB<∠AOE
C.∠AOB=∠FOD D.∠DOE>∠BOD
C
自学检测1(7分钟)
4、如图:OC、OD分别是∠AOB 、∠BOE的平分线,(1)如果∠AOB=70°, ∠BOE=60°,那么∠1+ ∠2=_____;
(2) 如果∠1+ ∠2 =55°,则∠AOE=_____.
65°
110°
A
O
B
C
E
D
1
2
3、(1)若OC是∠AOB的平分线,那么∠AOC =∠ __
∠AOB =2∠AOC =2∠__
O
A
C
B
(2)若OB是∠AOC的平分线,OC是∠BOD的平分线,你能从中找出哪些相等的角?
O
A
B
C
D
解:∠AOB= ∠BOC= ∠COD
∠AOC= ∠BOD
BOC
BOC
一. 1、度量法:
(1)、对“中”——角的顶点对量角器的中心;
(3)、读数——读出角的另一边所对的度数;
(2)、重合——角的一边与量角器的零线重合;
B
C
A
F
E
D
700
300
∠ABC > ∠DEF
一、比较两个角的大小的方法是什么?步骤是什么?
学生讨论、教师点拨:(3分钟)
二、角的大小与角的两边画出的长短有关吗?
B
A
O
(1) 将两个角的顶点及一边重合;
(2) 两个角的另一边落在重合一边的同侧;
(3)由两个角的另一边的位置确定两个角的大小.
2、叠合法:
C
D
E
∠ECD>∠AOB
O
A
B
D
C
E
∠ECD<∠AOB
A
O
B
C
D
E
∠ECD=∠AOB
二、角的大小与角的两边画出的长短有关吗?
1、角的大小与角的两边画出的长短_____________。
2、角的两边叉开的幅度越小,____________。
60°
60°
没有关系
角度就越小
自学指导2(1分钟)
认真阅读课本P136的内容,理解解题格式和方法。
学生自学,教师巡视(3分钟)
例1 如图,O是直线AB上一点,∠AOC=53 17′,求∠BOC的度数.
解:由题意可知,∠AOB是平角,
∠AOB=∠AOC+∠BOC,
所以∠BOC= ∠AOB-∠AOC
=180 - 53 17′
=126 43′
例2 把一个周角7等分,每一份是多少度的角 (精确到分)
解:360°÷7=51°+3°÷7
=51°+180′÷7
≈51°26′
所以,每份是51°26′
(P136T3)如图,O是直线AB上一点, OC是∠AOB的平分线, ∠COD=31 28′,求∠AOD的度数.
解:由题意可知,∠AOB是平角,
∵OC平分∠AOB
∴∠AOC= ∠AOB
= ×180°
= 90
∴∠AOD=∠AOC-∠COD
=90 -31 28′
=58 32′
自学检测2(7分钟)
∠ = 。
①两个锐角之和一定大于90°;
②两个钝角之和不一定大于180°;
③所有的直角都相等 ;
④ 平角大于 周角
当堂训练(15分钟)
1、下列说法中不正确的是_________.
①②④
2、
BE是 ABC的平分线
ABE
30°
A
B
C
D
E
60°
∠ABC=____+_____=
ABE
CBE
60°
3.(2021中考题)如图,∠AOB=20°,∠BOC=80°,OE是∠AOC的角平分线,则∠COE的度数为
( )
A.50° B.40° C.30° D.20°
A
4、(P140T9)如图,OB是∠AOC平分线,OD平分∠COE,
(1)如果∠AOB=40°,∠DOE=30°
那么∠AOE是多少度?
O
C
A
E
B
D
(变式)已知,如图,∠AOB=130°∠AOD=30°∠BOC=70°,
问:(1)OC是∠AOB的平分线吗?为什么?
(2)OD是∠AOC的平分线吗?为什么?
O
A
D
C
B
4、如图,OB是∠AOC平分线,OD平分∠COE,
(1)如果∠AOB=40°,∠DOE=30°
那么∠AOE是多少度?
O
C
A
E
B
D
∵OB是∠AOC平分线,∠AOB=40°
∴∠BOC=∠AOB=40°
∵OD平分∠COE,∠DOE=30°
∴∠DOC=∠DOE=30°
∴∠BOD=∠BOC+∠DOC=40°+30°=70°
5、已知,如图,∠AOB=130°∠AOD=30°∠BOC=70°,
问:(1)OC是∠AOB的平分线吗?为什么?
(2)OD是∠AOC的平分线吗?为什么?
O
A
D
C
B
解:(1)不是。理由如下:
∵∠AOB=130°,∠BOC=70°
∴∠AOC=∠AOB-∠BOC
=130°-70°=60°≠∠BOC
∴ OC不是∠AOB的平分线。
(2)是。理由如下:
∵∠AOB=130°,∠BOC=70°,∠AOD=30°
∴∠COD=∠AOB-∠BOC-∠AOD
=130°-70°-30°
=30°
∴∠COD=∠AOD,所以OD是∠AOC的平分线。
(选做题)、如图所示,将一张长方形纸斜折过去,使顶点A落在A’处,BC为折痕,然后把BE折过去,使之与A’B重合,折痕为BD那么两折痕BC、BD间的夹角是多少度?
A
A’
B
C
E
D
E’
解:∵ ∠CBA与∠CBA’折叠重合
∴ ∠CBA=∠CBA’
∵ ∠EBD与∠E’BD折叠重合
∴ ∠EBD= ∠ E’BD
∵ ∠CBA+∠CBA’+ ∠EBD+ ∠ E’BD=180°
∴ ∠CBA’+ ∠ E’BD= ×180°=90°
∴ ∠CBD = ∠CBA’+ ∠ E’BD =90°
正本作业 P136 练习 T3
板书设计
1、如何比较两个角的大小:
(1). 度量法
(2). 叠合法
2、角的平分线:
∵
一条射线把一个角分成两个相等的角,则这条射线叫这个角的角平分线。
符号语言
O
A
C
B
思考:下图中共有几个角?
它们有什么关系?
完成下列问题:
1、图中共有__个角,它们分别是______________
2、∠AOB=____+_____
3、∠AOC=____-_____
4、∠BOC=____-_____
3
∠AOB ∠AOC ∠BOC
∠AOC ∠BOC
∠AOB ∠BOC
∠AOB ∠AOC
利用一副三角板,你能画出哪些度数的角?这些角有什么规律?
α
α
α
角的三等分线
α
α
α
α
角的四等分线
⌒
⌒
2
1
O
A
C
B
几何语言
∵∠1=∠2
∴ OC平分∠AOB
一条射线把一个角分成两个相等的角,则这条射线叫这个角的角平分线。
角平分线
角平分线的性质
几何语言
∵OC平分∠AOB
∴∠1=∠2
(或∠AOB= 2∠1 =2∠2)
正本答案
∵∠AOB=180°,
0C是∠AOB的平分线,
∴∠AOC=∠BOC= ∠AOB=90°
∴∠AOD=∠AOC-∠COD
=90°-31°28′
=58°32′
