人教版数学七年级上册4.3.3余角和补角 课件(共20张PPT)
文档属性
| 名称 | 人教版数学七年级上册4.3.3余角和补角 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 522.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 10:31:14 | ||
图片预览







文档简介
(共20张PPT)
课前提问(1分钟)
1、如何比较两个角的大小:
(1). 度量法
(2). 叠合法
2、角的平分线:
⌒
⌒
O
A
C
B
第四章:几何图形初步
4.3.3 余角和补角
人教版七年级数学上册
议课小组:第一组
议课时间:2022.10.23
授课时间:2022.12.
学习目标(1分钟)
1、了解两个角互余和互补的意义,并掌握余角和补角的性质。 (重点)
2、理解方位角的概念,会用角描述方向。(难点)
中考考点:余角和补角的性质.
阅读课本P137例3之前,并思考下列问题:
1、余角的定义
如果两个角的和等于___________,就说这两个角互为
余角,即其中每一个角是另一个角的余角.
2、补角的定义
如果两个角的和等于___________,就说这两个角互为
补角,即其中一个角是另一个角的补角.
自学指导1(1分钟)
学生自学,教师巡视(4分钟)
90 (直角)
3、余角、补角的性质:
同角(等角)的余角相等.
同角(等角)的补角相等.
180 (平角)
自学检测1(7分钟)
1.如果α与β互为余角,那么( )
A.α+β=180° B.α-β=180°
C.α-β=90° D.α+β=90°
D
2.已知∠1+∠2=180°,∠3+∠4=180°,
如果∠1=∠3,那么∠2=∠4,依据是( )
A.同角的余角相等 B.同角的补角相等
C.等角的余角相等 D.等角的补角相等
D
152°31′
4.(2021 兰州)已知∠α=60°,∠α与∠β互余,∠β与∠γ互补,则∠γ的值等于 。
150°
3.(2021 雁塔)如图,点O为直线AB上一点,∠COB=27°29′,则∠1= 。
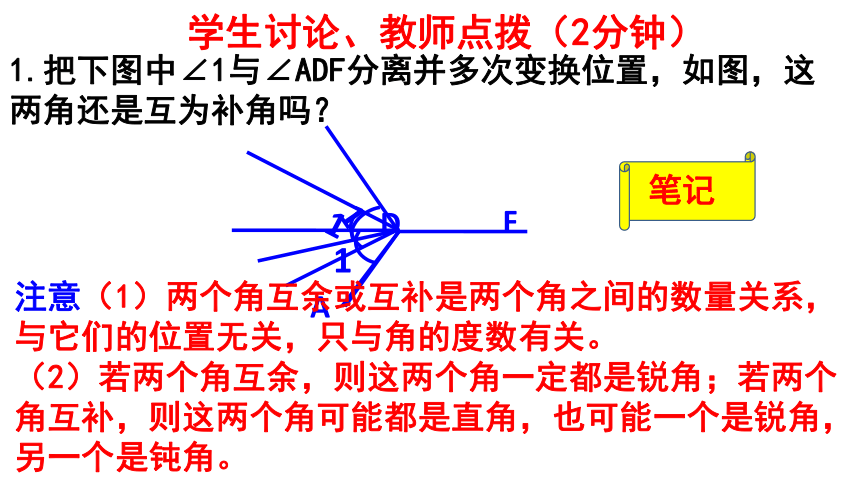
1.把下图中∠1与∠ADF分离并多次变换位置,如图,这两角还是互为补角吗?
1
A
D
F
1
1
学生讨论、教师点拨(2分钟)
注意(1)两个角互余或互补是两个角之间的数量关系,与它们的位置无关,只与角的度数有关。
(2)若两个角互余,则这两个角一定都是锐角;若两个角互补,则这两个角可能都是直角,也可能一个是锐角,另一个是钝角。
笔记
自学指导2(1分钟)
阅读课本例3和例4,思考下列问题.
学生自学,教师巡视(5分钟)
1.有时以 、 方向为基准,描述物体运动的方向.
2.表示方向的角 在航行、测绘等工作中经常
用到.
正北
正南
(方位角)
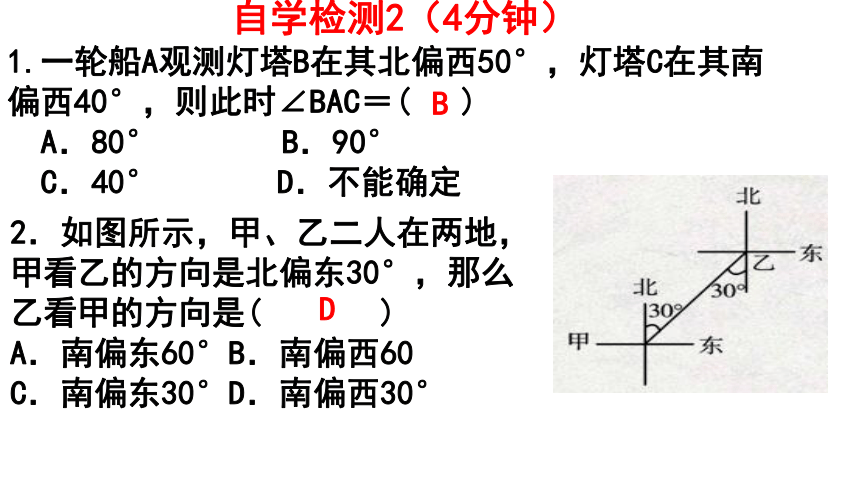
自学检测2(4分钟)
1.一轮船A观测灯塔B在其北偏西50°,灯塔C在其南
偏西40°,则此时∠BAC=( )
A.80° B.90°
C.40° D.不能确定
B
2.如图所示,甲、乙二人在两地,甲看乙的方向是北偏东30°,那么乙看甲的方向是( )
A.南偏东60°B.南偏西60
C.南偏东30°D.南偏西30°
D
3.如图,OA的方向是北偏东15°,OB的方向是北偏西40°,若∠AOC=∠AOB,则OC的方向是 .
北偏东70°
课堂小结(1分钟)
互为余角 互为补角
对应图形
数量关系
性 质
1
2
1
2
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等.
同角或等角的补角相等.
当堂训练(15分钟)
1.若∠1与∠2互余,∠2与∠3互余,则_____=______,
根据是________ .
2.若∠3与∠4互补,∠6与∠5互补,且∠3=∠6,
则_____=______,根据是__________.
同角的余角相等
等角的补角相等
∠1
∠3
∠4
∠5
3.如图,直线a与直线c相交于点O,∠1的余角的度数
是( )
A.60° B.50°
C.40° D.30°
A
4.(2019春 渝中区校级月考)∠α的余角为65°,则∠α的补角为( )
A.35° B.25° C.155° D.65°
C
(变式)若∠1与∠2互余,∠2与∠3互补,∠1+∠3=
150°,则∠2= 。
60°
6.已知一个角的补角比这个角的余角的3倍少18°,求这个角的度数.
解:设这个角的度数为x°,则它的余角为(90°-x°),
补角为(180°-x°),由题意,得
180-x=3(90-x)-18 解得x=36
因此,这个角的度数为36°
5.如图,甲从A点出发向北偏东70°方
向走50米至B点,乙从A出发向南偏西
15°方向走80米至点C,则∠BAC的度数
为( )
C
A.85° B.160° C.125° D.105 °
正本作业(课本第139页,练习第2,3题)
(选做题)如图,OD平分∠BOC,OE平分∠AOC,
∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE与
∠AOB是否互补,并说明理由.
解:(1)∠AOB=∠BOC+∠AOC
=70°+50°
=120°
其补角为180°-∠AOB=180°-120°=60°
(选做题)如图,OD平分∠BOC,OE平分∠AOC,
∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE与
∠AOB是否互补,并说明理由.
理由:∵∠DOE=∠DOC+∠COE
=35°+25°
=60°
∴∠DOE+∠AOB=60°+120°
=180°
∴∠DOE与∠AOB互补
板书设计
4.3.3 余角和补角
互为余角 互为补角
对应图形
数量关系
性 质
1
2
1
2
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等.
同角或等角的补角相等.
解: ∵ A,O,B在同一直线上,
∴ ∠AOC和∠BOC互为补角。
又∵射线OD和射线OE分别平分∠AOC∠BOC,
∴ ∠COD +∠COE=∠AOC+ ∠BOC
= (∠AOC+∠BOC)
=90°
∴ ∠COD 和∠COE互为余角
同理, ∠AOD 和∠BOE,∠AOD 和∠COE ,
∠COD 和∠BOE也互为余角.
例 3 如图,A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和 ∠BOC,图中哪些角互为余角?
例4:如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B,货轮C和海岛D方向的射线.
O
●
东
南
西
北
● A
60°
射线OA的方向就是南偏东60°,即灯塔A所在的方向。
● B
● D
射线OB的方向就是北偏东40°,即客轮B所在的方向。
C ●
40°
10°
射线OC的方向就是南偏西10°,即货轮C所在的方向。
射线OD的方向就是南偏西45°,即海岛D所在的方向。
45°
证明: ∵∠1与∠2 , ∠3都互为补角,
∴ ∠1+ ∠2 = 180 °,
∠1+ ∠3 = 180 °
∴∠2 = 180° -∠1
∠3= 180 °-∠1
∴∠2 = ∠3
同理可证得,∠1与∠2 , ∠3都互为余角时,
∠2 = ∠3
正本作业
2.解: 它的余角:90°- 70°39′=19°21′
它的补角:180°- 70°39′=109°21′
3.解: ∵ ∠a的补角为180°- ∠a
∴ 3 ∠a = 180°- ∠a
4∠a = 180°
∠a = 45°
课前提问(1分钟)
1、如何比较两个角的大小:
(1). 度量法
(2). 叠合法
2、角的平分线:
⌒
⌒
O
A
C
B
第四章:几何图形初步
4.3.3 余角和补角
人教版七年级数学上册
议课小组:第一组
议课时间:2022.10.23
授课时间:2022.12.
学习目标(1分钟)
1、了解两个角互余和互补的意义,并掌握余角和补角的性质。 (重点)
2、理解方位角的概念,会用角描述方向。(难点)
中考考点:余角和补角的性质.
阅读课本P137例3之前,并思考下列问题:
1、余角的定义
如果两个角的和等于___________,就说这两个角互为
余角,即其中每一个角是另一个角的余角.
2、补角的定义
如果两个角的和等于___________,就说这两个角互为
补角,即其中一个角是另一个角的补角.
自学指导1(1分钟)
学生自学,教师巡视(4分钟)
90 (直角)
3、余角、补角的性质:
同角(等角)的余角相等.
同角(等角)的补角相等.
180 (平角)
自学检测1(7分钟)
1.如果α与β互为余角,那么( )
A.α+β=180° B.α-β=180°
C.α-β=90° D.α+β=90°
D
2.已知∠1+∠2=180°,∠3+∠4=180°,
如果∠1=∠3,那么∠2=∠4,依据是( )
A.同角的余角相等 B.同角的补角相等
C.等角的余角相等 D.等角的补角相等
D
152°31′
4.(2021 兰州)已知∠α=60°,∠α与∠β互余,∠β与∠γ互补,则∠γ的值等于 。
150°
3.(2021 雁塔)如图,点O为直线AB上一点,∠COB=27°29′,则∠1= 。
1.把下图中∠1与∠ADF分离并多次变换位置,如图,这两角还是互为补角吗?
1
A
D
F
1
1
学生讨论、教师点拨(2分钟)
注意(1)两个角互余或互补是两个角之间的数量关系,与它们的位置无关,只与角的度数有关。
(2)若两个角互余,则这两个角一定都是锐角;若两个角互补,则这两个角可能都是直角,也可能一个是锐角,另一个是钝角。
笔记
自学指导2(1分钟)
阅读课本例3和例4,思考下列问题.
学生自学,教师巡视(5分钟)
1.有时以 、 方向为基准,描述物体运动的方向.
2.表示方向的角 在航行、测绘等工作中经常
用到.
正北
正南
(方位角)
自学检测2(4分钟)
1.一轮船A观测灯塔B在其北偏西50°,灯塔C在其南
偏西40°,则此时∠BAC=( )
A.80° B.90°
C.40° D.不能确定
B
2.如图所示,甲、乙二人在两地,甲看乙的方向是北偏东30°,那么乙看甲的方向是( )
A.南偏东60°B.南偏西60
C.南偏东30°D.南偏西30°
D
3.如图,OA的方向是北偏东15°,OB的方向是北偏西40°,若∠AOC=∠AOB,则OC的方向是 .
北偏东70°
课堂小结(1分钟)
互为余角 互为补角
对应图形
数量关系
性 质
1
2
1
2
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等.
同角或等角的补角相等.
当堂训练(15分钟)
1.若∠1与∠2互余,∠2与∠3互余,则_____=______,
根据是________ .
2.若∠3与∠4互补,∠6与∠5互补,且∠3=∠6,
则_____=______,根据是__________.
同角的余角相等
等角的补角相等
∠1
∠3
∠4
∠5
3.如图,直线a与直线c相交于点O,∠1的余角的度数
是( )
A.60° B.50°
C.40° D.30°
A
4.(2019春 渝中区校级月考)∠α的余角为65°,则∠α的补角为( )
A.35° B.25° C.155° D.65°
C
(变式)若∠1与∠2互余,∠2与∠3互补,∠1+∠3=
150°,则∠2= 。
60°
6.已知一个角的补角比这个角的余角的3倍少18°,求这个角的度数.
解:设这个角的度数为x°,则它的余角为(90°-x°),
补角为(180°-x°),由题意,得
180-x=3(90-x)-18 解得x=36
因此,这个角的度数为36°
5.如图,甲从A点出发向北偏东70°方
向走50米至B点,乙从A出发向南偏西
15°方向走80米至点C,则∠BAC的度数
为( )
C
A.85° B.160° C.125° D.105 °
正本作业(课本第139页,练习第2,3题)
(选做题)如图,OD平分∠BOC,OE平分∠AOC,
∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE与
∠AOB是否互补,并说明理由.
解:(1)∠AOB=∠BOC+∠AOC
=70°+50°
=120°
其补角为180°-∠AOB=180°-120°=60°
(选做题)如图,OD平分∠BOC,OE平分∠AOC,
∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE与
∠AOB是否互补,并说明理由.
理由:∵∠DOE=∠DOC+∠COE
=35°+25°
=60°
∴∠DOE+∠AOB=60°+120°
=180°
∴∠DOE与∠AOB互补
板书设计
4.3.3 余角和补角
互为余角 互为补角
对应图形
数量关系
性 质
1
2
1
2
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等.
同角或等角的补角相等.
解: ∵ A,O,B在同一直线上,
∴ ∠AOC和∠BOC互为补角。
又∵射线OD和射线OE分别平分∠AOC∠BOC,
∴ ∠COD +∠COE=∠AOC+ ∠BOC
= (∠AOC+∠BOC)
=90°
∴ ∠COD 和∠COE互为余角
同理, ∠AOD 和∠BOE,∠AOD 和∠COE ,
∠COD 和∠BOE也互为余角.
例 3 如图,A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和 ∠BOC,图中哪些角互为余角?
例4:如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B,货轮C和海岛D方向的射线.
O
●
东
南
西
北
● A
60°
射线OA的方向就是南偏东60°,即灯塔A所在的方向。
● B
● D
射线OB的方向就是北偏东40°,即客轮B所在的方向。
C ●
40°
10°
射线OC的方向就是南偏西10°,即货轮C所在的方向。
射线OD的方向就是南偏西45°,即海岛D所在的方向。
45°
证明: ∵∠1与∠2 , ∠3都互为补角,
∴ ∠1+ ∠2 = 180 °,
∠1+ ∠3 = 180 °
∴∠2 = 180° -∠1
∠3= 180 °-∠1
∴∠2 = ∠3
同理可证得,∠1与∠2 , ∠3都互为余角时,
∠2 = ∠3
正本作业
2.解: 它的余角:90°- 70°39′=19°21′
它的补角:180°- 70°39′=109°21′
3.解: ∵ ∠a的补角为180°- ∠a
∴ 3 ∠a = 180°- ∠a
4∠a = 180°
∠a = 45°
