人教版七年级上册3.4 一元一次方程的应用(第1课时)(共20张PPT)
文档属性
| 名称 | 人教版七年级上册3.4 一元一次方程的应用(第1课时)(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 10.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
第1课时 产品配套问题和工程问题
学习目标:
1.掌握产品配套问题、工程问题中常见的数量关系.
2.掌握用一元一次方程解决实际问题的基本过程.
3.弄清题意,用列方程解决实际问题是本课重点,寻找实际问题中的等量关系,建立数学模型.
目 录
壹
贰
叁
肆
温故知新
新知探究
新知巩固
课堂收获
壹
温故知新
1、解下列方程:
壹
2、你能解决吗?
温故知新
近来我市要修一条公路,公路大约长120千米,今天一早,有两个工程队找到了局长,甲工程队说:“包给我们,保证30天完成”;乙工程队说:“包给我们,保证20天就完成”.如果你是负责的领导,会怎么办呢?请积极发表意见。
贰
新知探究
一、产品配套问题
某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
请先独立探究,然后互相交流
贰
新知探究
一、产品配套问题
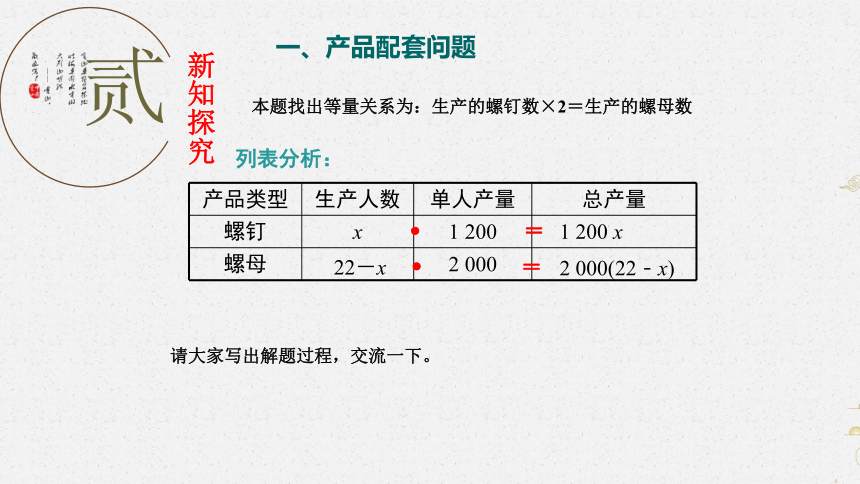
列表分析:
产品类型 生产人数 单人产量 总产量
螺钉 x 1 200
螺母 2 000
·
·
22-x
1 200 x
2 000(22-x)
=
=
本题找出等量关系为:生产的螺钉数×2=生产的螺母数
请大家写出解题过程,交流一下。
贰
新知探究
一、产品配套问题
解:设应安排x名工人生产螺钉,(22-x)名工人生产螺母.
列方程
2 000(22-x)=2×1 200x .
解方程,得
5(22-x)=6x,
110-5x=6x,
x=10.
22-x=12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
根据:螺母总量=螺钉总量×2
动手一试
某种设备由一个甲部件和三个乙部件构成. 用1kg材料可做40个甲部件或240个乙部件.现要用9kg材料制作这种设备,应该用多少材料做甲部件,多少材料做乙部件,恰好配成这种设备多少套?
分析:根据题意知乙部件的数量是甲部件数量的3倍这一等量关系式得方程.
解:设应用xkg材料做甲部件,则应用(9-x)kg材料做乙部件,根据题意,列方程得:
3×40x=(9-x) ×240
解方程,得
x=(9-x) ×2
3x=18
x=6
答:应该用6kg材料做甲部件,应用3kg材料做乙部件,可以做240套该设备。
动手一试
方法规律: 生产配套问题通常从配套后各量之间的倍、分关系寻找相等关系,建立方程.
贰
新知探究
二、工程问题
整理一批图书:由一个人做要40 h完成.现计划由一部分人先做4 h,然后增加2人与他们一起做8 h,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作
请思考:(1)由一个人要做40小时完成,这句话的作用
(2)根据题意,整项工作分成几部分 你如何做此题?
贰
新知探究
二、工程问题
整理一批图书:由一个人做要40 h完成.现计划由一部分人先做4 h,然后增加2人与他们一起做8 h,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作
分析:把工作量看作单位“1‘”,则人均的工作效率(1个人1小时完成的工作量)为 ,x人先做4小时完成的工作量为,增加2人后再做8小时完成的工作量为,这两个工作量之和应等于总工作量。
人均效率 人数 时间 工作量
前一部分工作 x 4
后一部分工作 x+2 8
·
=
·
=
工作量之和等于总工作量1
贰
新知探究
二、工程问题
解:设先安排 x 人做4 h,根据题意得等量关系:
可列方程
前部分工作总量+后部分工作总量=总工作量1
请大家把剩下的过程补全并交流一下。
动手一试
一个道路工程,甲队单独施工9天完成,乙队单独做24天完成.现在甲乙两队共同施工3天,因甲另有任务,剩下的工程由乙队完成,问乙队还需几天才能完成?
分析:首先设乙队还需x天才能完成,由题意可得等量关系:甲队干三天的工作量+乙队干(x+3)天的工作量=1,根据等量关系列出方程,求解即可.
解:设乙队还需x天才能完成,由题意得
×3+(3+x)=1,
解得x=13.
答:乙队还需13天才能完成.
动手一试
方法总结:找到等量关系是解决问题的关键.本题主要考查的等量关系为:工作效率×工作时间=工作总量,当题中没有一些必须的量时,为了简便,应设其为1.
叁
新知巩固
解决工程问题的思路:
1.三个基本量:
工程问题中的三个基本量:工作量、工作效率、工作时间,
它们之间的关系是:工作量=工作效率×工作时间.
若把工作量看作1,则工作效率=
2.相等关系:
(1)按工作时间,各时间段的工作量之和=完成的工作量.
(2)按工作者,若一项工作有甲、乙两人参与,则甲的工作量
+乙的工作量=完成的工作量.
叁
新知巩固
1、某水利工地派48人去挖土和运土,如果每人每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走
动手做一做
18人挖土,30人运土
2、一项工作,甲独做需18天,乙独做需24天,如果两人合做8天后,余下的工作再由甲独做x天完成,那么所列方程为____________.
3、整理一批图书,由一个人做要40 h完成,现计划由2人先做4 h,然后增加若干人与他们一起又做4 h完成了这项工作,问增加了多少人
增加了8人
4、用白铁皮做罐头盒,每张铁皮可制盒身10个或制盒底30个,一个盒身与两个盒底配成一套罐头盒.现有100张白铁皮,用多少张制盒身,多少张制盒底,可以既使做出的盒身和盒底配套,又能充分地利用白铁皮
60张做盒身,40张做盒底
肆
课堂收获
1、通过学习你认为用一元一次方程解决实际问题的过程和步骤是怎样的?
肆
课堂收获
2、在解决配套、工程分配等问题方面你获得了哪些经验 这些问题中的相等关系有什么特点 请积极发表意见。
作业:106页习题3.4第2、3、4题
谢 谢!
第1课时 产品配套问题和工程问题
学习目标:
1.掌握产品配套问题、工程问题中常见的数量关系.
2.掌握用一元一次方程解决实际问题的基本过程.
3.弄清题意,用列方程解决实际问题是本课重点,寻找实际问题中的等量关系,建立数学模型.
目 录
壹
贰
叁
肆
温故知新
新知探究
新知巩固
课堂收获
壹
温故知新
1、解下列方程:
壹
2、你能解决吗?
温故知新
近来我市要修一条公路,公路大约长120千米,今天一早,有两个工程队找到了局长,甲工程队说:“包给我们,保证30天完成”;乙工程队说:“包给我们,保证20天就完成”.如果你是负责的领导,会怎么办呢?请积极发表意见。
贰
新知探究
一、产品配套问题
某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
请先独立探究,然后互相交流
贰
新知探究
一、产品配套问题
列表分析:
产品类型 生产人数 单人产量 总产量
螺钉 x 1 200
螺母 2 000
·
·
22-x
1 200 x
2 000(22-x)
=
=
本题找出等量关系为:生产的螺钉数×2=生产的螺母数
请大家写出解题过程,交流一下。
贰
新知探究
一、产品配套问题
解:设应安排x名工人生产螺钉,(22-x)名工人生产螺母.
列方程
2 000(22-x)=2×1 200x .
解方程,得
5(22-x)=6x,
110-5x=6x,
x=10.
22-x=12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
根据:螺母总量=螺钉总量×2
动手一试
某种设备由一个甲部件和三个乙部件构成. 用1kg材料可做40个甲部件或240个乙部件.现要用9kg材料制作这种设备,应该用多少材料做甲部件,多少材料做乙部件,恰好配成这种设备多少套?
分析:根据题意知乙部件的数量是甲部件数量的3倍这一等量关系式得方程.
解:设应用xkg材料做甲部件,则应用(9-x)kg材料做乙部件,根据题意,列方程得:
3×40x=(9-x) ×240
解方程,得
x=(9-x) ×2
3x=18
x=6
答:应该用6kg材料做甲部件,应用3kg材料做乙部件,可以做240套该设备。
动手一试
方法规律: 生产配套问题通常从配套后各量之间的倍、分关系寻找相等关系,建立方程.
贰
新知探究
二、工程问题
整理一批图书:由一个人做要40 h完成.现计划由一部分人先做4 h,然后增加2人与他们一起做8 h,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作
请思考:(1)由一个人要做40小时完成,这句话的作用
(2)根据题意,整项工作分成几部分 你如何做此题?
贰
新知探究
二、工程问题
整理一批图书:由一个人做要40 h完成.现计划由一部分人先做4 h,然后增加2人与他们一起做8 h,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作
分析:把工作量看作单位“1‘”,则人均的工作效率(1个人1小时完成的工作量)为 ,x人先做4小时完成的工作量为,增加2人后再做8小时完成的工作量为,这两个工作量之和应等于总工作量。
人均效率 人数 时间 工作量
前一部分工作 x 4
后一部分工作 x+2 8
·
=
·
=
工作量之和等于总工作量1
贰
新知探究
二、工程问题
解:设先安排 x 人做4 h,根据题意得等量关系:
可列方程
前部分工作总量+后部分工作总量=总工作量1
请大家把剩下的过程补全并交流一下。
动手一试
一个道路工程,甲队单独施工9天完成,乙队单独做24天完成.现在甲乙两队共同施工3天,因甲另有任务,剩下的工程由乙队完成,问乙队还需几天才能完成?
分析:首先设乙队还需x天才能完成,由题意可得等量关系:甲队干三天的工作量+乙队干(x+3)天的工作量=1,根据等量关系列出方程,求解即可.
解:设乙队还需x天才能完成,由题意得
×3+(3+x)=1,
解得x=13.
答:乙队还需13天才能完成.
动手一试
方法总结:找到等量关系是解决问题的关键.本题主要考查的等量关系为:工作效率×工作时间=工作总量,当题中没有一些必须的量时,为了简便,应设其为1.
叁
新知巩固
解决工程问题的思路:
1.三个基本量:
工程问题中的三个基本量:工作量、工作效率、工作时间,
它们之间的关系是:工作量=工作效率×工作时间.
若把工作量看作1,则工作效率=
2.相等关系:
(1)按工作时间,各时间段的工作量之和=完成的工作量.
(2)按工作者,若一项工作有甲、乙两人参与,则甲的工作量
+乙的工作量=完成的工作量.
叁
新知巩固
1、某水利工地派48人去挖土和运土,如果每人每天平均挖土5方或运土3方,那么应怎样安排人员,正好能使挖出的土及时运走
动手做一做
18人挖土,30人运土
2、一项工作,甲独做需18天,乙独做需24天,如果两人合做8天后,余下的工作再由甲独做x天完成,那么所列方程为____________.
3、整理一批图书,由一个人做要40 h完成,现计划由2人先做4 h,然后增加若干人与他们一起又做4 h完成了这项工作,问增加了多少人
增加了8人
4、用白铁皮做罐头盒,每张铁皮可制盒身10个或制盒底30个,一个盒身与两个盒底配成一套罐头盒.现有100张白铁皮,用多少张制盒身,多少张制盒底,可以既使做出的盒身和盒底配套,又能充分地利用白铁皮
60张做盒身,40张做盒底
肆
课堂收获
1、通过学习你认为用一元一次方程解决实际问题的过程和步骤是怎样的?
肆
课堂收获
2、在解决配套、工程分配等问题方面你获得了哪些经验 这些问题中的相等关系有什么特点 请积极发表意见。
作业:106页习题3.4第2、3、4题
谢 谢!
