沪科版(2012)九年级数学上册期中复习试卷(word版含答案)
文档属性
| 名称 | 沪科版(2012)九年级数学上册期中复习试卷(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 917.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 00:00:00 | ||
图片预览


文档简介
沪科版(2012)九年级数学上册期中复习试卷
姓名:___________班级:_____考号:_____
一、选择题(每题3分,共24分)
1.下列函数中,y是x的二次函数的是 ( )
A. B. C. D.
2.已知,则下列比例式成立的是 ( )
A. B. C. D.
3.将抛物线先向左平移2个单位,再向上平移3个单位后,得到( )
A. B.
C. D.
4.如图,在△ABC中,,若AD∶DB=3∶2,AE=6cm,则AC的长为( )
A.6cm B.5cm C.4cm D.10cm
5.如图,在中,是斜边上的高,若,,则的长为 ( )
A.8 B.10 C.9 D.12
6.在平面直角坐标系中,已知抛物线与关于y轴对称,则的值为 ( )
A.6 B. C. D.
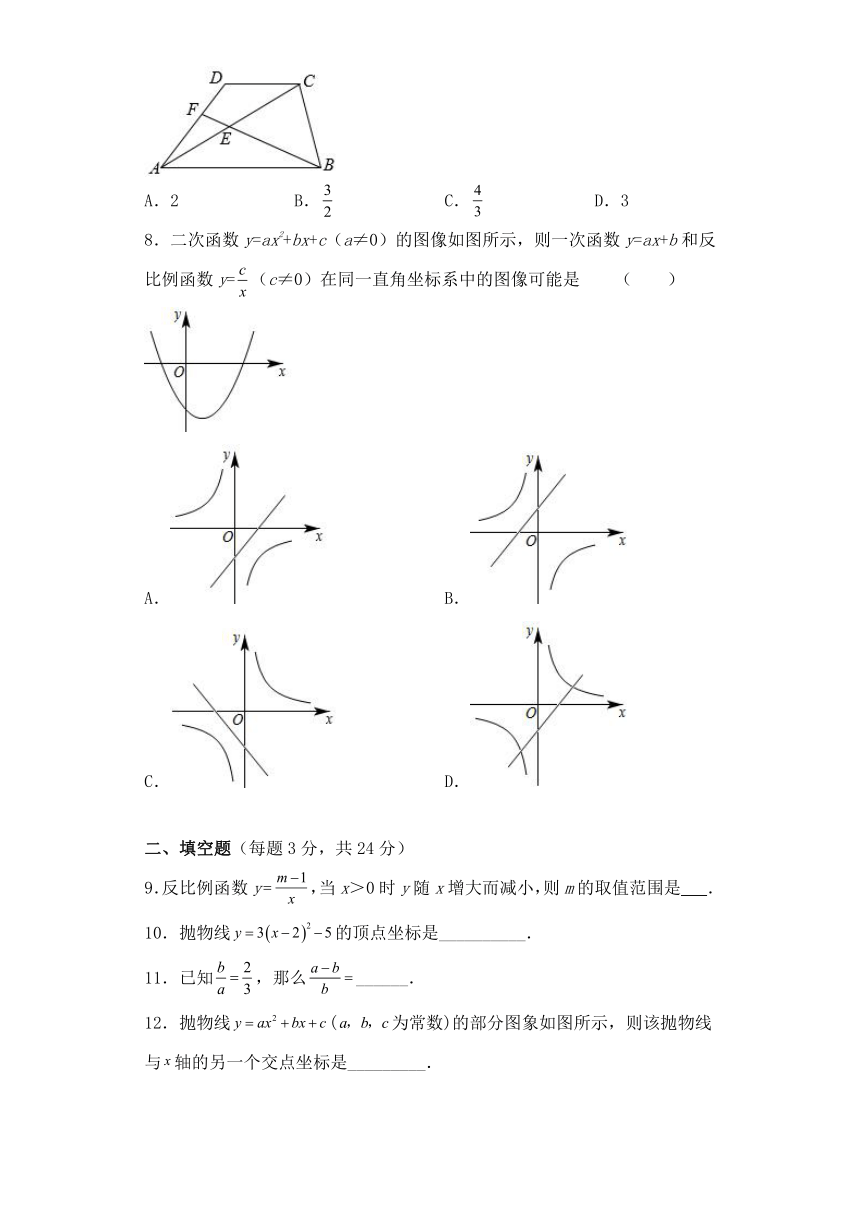
7.如图,四边形的面积为18,,且,E为的中点,的延长线交于F,则的面积是 ( )
A.2 B. C. D.3
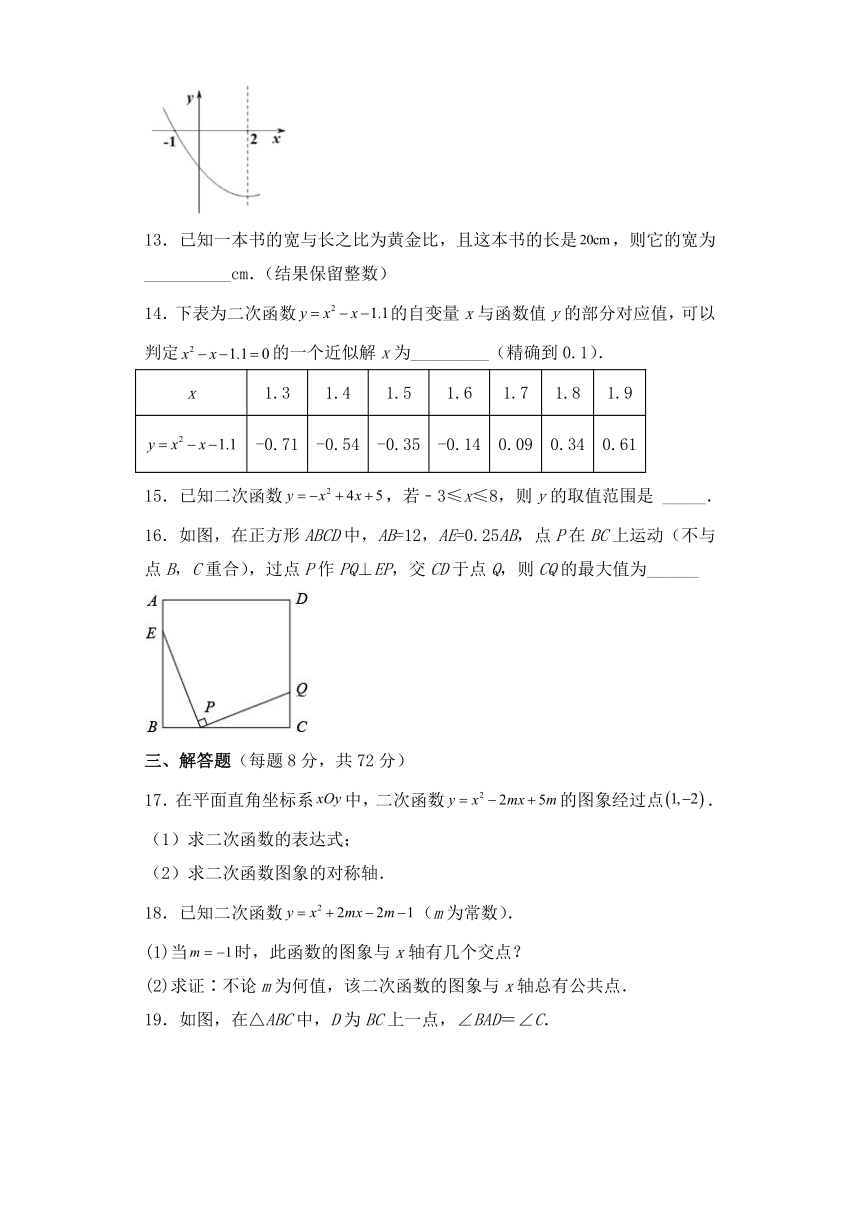
8.二次函数y=ax2+bx+c(a≠0)的图像如图所示,则一次函数y=ax+b和反比例函数y=(c≠0)在同一直角坐标系中的图像可能是 ( )
A. B.
C. D.
二、填空题(每题3分,共24分)
9.反比例函数y,当x>0时y随x增大而减小,则m的取值范围是 .
10.抛物线的顶点坐标是__________.
11.已知,那么______.
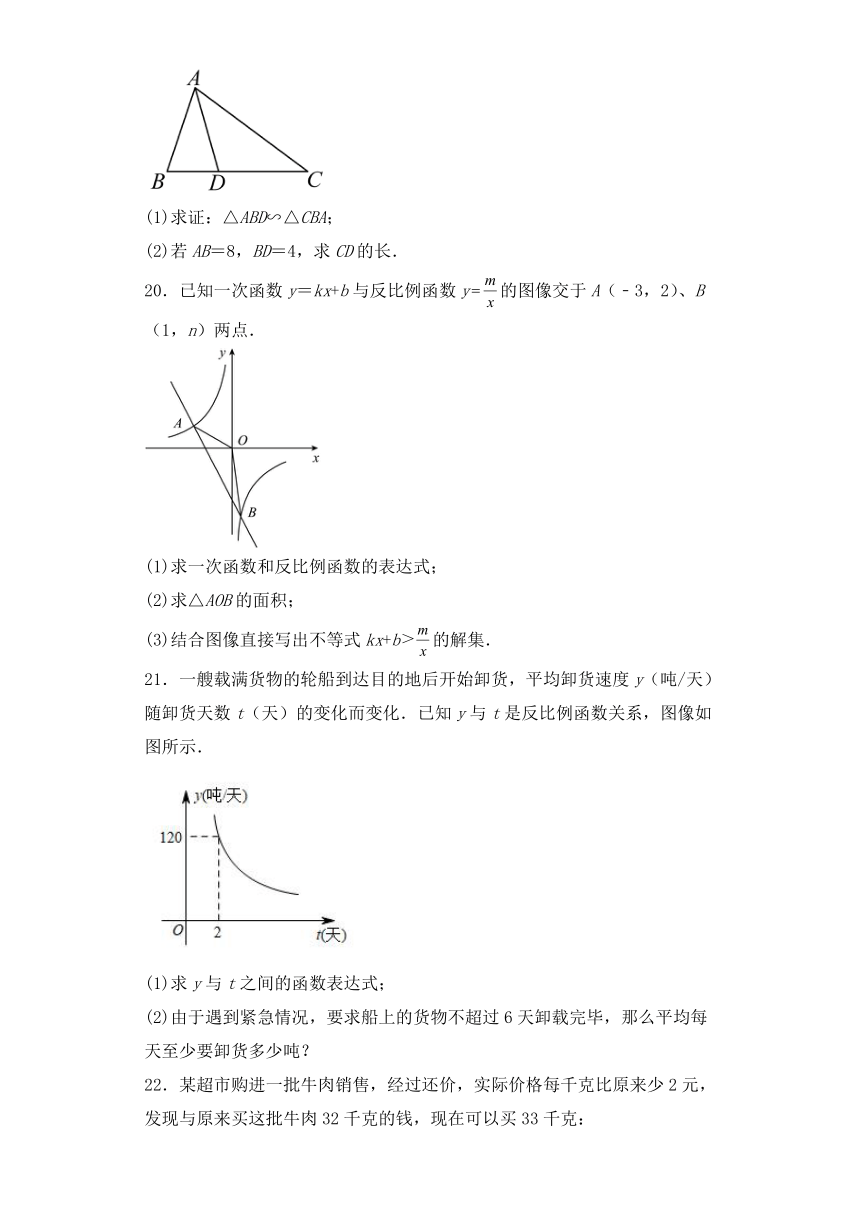
12.抛物线(为常数)的部分图象如图所示,则该抛物线与轴的另一个交点坐标是_________.
13.已知一本书的宽与长之比为黄金比,且这本书的长是,则它的宽为__________cm.(结果保留整数)
14.下表为二次函数的自变量x与函数值y的部分对应值,可以判定的一个近似解x为_________(精确到0.1).
x 1.3 1.4 1.5 1.6 1.7 1.8 1.9
-0.71 -0.54 -0.35 -0.14 0.09 0.34 0.61
15.已知二次函数,若﹣3≤x≤8,则y的取值范围是 _____.
16.如图,在正方形ABCD中,AB=12,AE=0.25AB,点P在BC上运动(不与点B,C重合),过点P作PQ⊥EP,交CD于点Q,则CQ的最大值为______
三、解答题(每题8分,共72分)
17.在平面直角坐标系中,二次函数的图象经过点.
(1)求二次函数的表达式;
(2)求二次函数图象的对称轴.
18.已知二次函数(m为常数).
(1)当时,此函数的图象与x轴有几个交点?
(2)求证∶不论m为何值,该二次函数的图象与x轴总有公共点.
19.如图,在△ABC中,D为BC上一点,∠BAD=∠C.
(1)求证:△ABD∽△CBA;
(2)若AB=8,BD=4,求CD的长.
20.已知一次函数y=kx+b与反比例函数y的图像交于A(﹣3,2)、B(1,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)结合图像直接写出不等式kx+b的解集.
21.一艘载满货物的轮船到达目的地后开始卸货,平均卸货速度y(吨/天)随卸货天数t(天)的变化而变化.已知y与t是反比例函数关系,图像如图所示.
(1)求y与t之间的函数表达式;
(2)由于遇到紧急情况,要求船上的货物不超过6天卸载完毕,那么平均每天至少要卸货多少吨?
22.某超市购进一批牛肉销售,经过还价,实际价格每千克比原来少2元,发现与原来买这批牛肉32千克的钱,现在可以买33千克:
(1)现在实际购进这批牛肉每千克多少元?
(2)若这批牛肉的销售量y(千克)与销售单价x(元/千克)满足,那么这批牛肉的销售单价定为多少时,能获得最大利润?最大利润是多少?(利润=销售收入-进货金额)
23.如图,在Rt中,,,,点P从点A出发,以1cm/s的速度沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.设点P、Q运动时间为.当与相似时,的值是多少?
24.如图所示,已知抛物线与一次函数y=kx+b的图像相交于 ,两点,点P是抛物线上不与A,B重合的一个动点,点Q是y轴上的一个动点
(1)直接写出抛物线和一次函数的解析式及关于x的不等式的解集;
(2)当点P在直线上方时,求出面积最大时点P的坐标;
(3)是否存在以P,Q,A,B为顶点的四边形是平行四边形?若存在,直接写出P的坐标;若不存在,请说明理由.
25.如图,平面直角坐标系中,四边形是平行四边形,,动点P从O出发向A以每秒1个单位的速度移动,动点Q从A出发沿的路径以每秒2个单位的速度移动,当其中一个点运动到终点时运动停止,过点P作x轴的垂线,交线段或线段于点E,连接,设运动时间为t秒.
(1)求直线解析式;
(2)设的面积为S,求S关于t的函数解析式,并写出定义域;
(3)在运动过程中,能否为等腰三角形?若能,直接写出t的值,若不能,请说明理由.
参考答案:
1.
解:A、是二次函数,故符合题意;
B、是一次函数,故不合题意;
C、含有分式,不是二次函数,故不合题意;
D、含有分式,不是二次函数,故不合题意.
故选:A.
2.
A.变成等积式是:,故不符合题意;
B.变成等积式是:,故符合题意;
C.变成等积式是:,故不符合题意;
D.变成等积式是:,故不符合题意.
故选:B.
3.
解:抛物线向左平移2个单位.再向上平移3个单位,
∴平移后的抛物线解析式为.
故选:A.
4.
解∶∵,AD∶DB=3:2,
∴AD∶DB=AE∶EC=3∶2,
∵AE=6cm,
∴6∶EC=3∶2,
∴EC=4cm,
∴AC=AE+EC=10cm.
故选:D
5.
解:如图所示,
∵,,
∴,,
∴,,
∴,
∴,即,且,,
∴,
故选:.
6.
解:∵,抛物线与关于y轴对称,
∴,
∴,,
∴,
故选:B
7.
解:作辅助线如下:延长EF交CD的延长线于点M,
∵,
∴∠ABE=∠DME, ∠BAE=∠MCE,
∵E为的中点,
∴AE=CE,
∴△ABE△CME,
∴CM=AB.
∵,
∴,
∴CD=MD=,
∴△ADC的面积=×△ABC的面积,
∵E为AC的中点,
∴△AEB的面积=△ECB的面积=×△ABC的面积,
∴△ADC的面积=△AEB的面积=△ECB的面积,
∵四边形的面积为18,
∴△ADC的面积=△AEB的面积=△ECB的面积=×四边形ABCD的面积=×18=6.
∵,
∴∠ABF=∠DMF, ∠BAF=∠MDF,
∴△MDF∽△FAB,
∵MD=AB,
∴△MDF的面积=×△AFB的面积,
∵假设△AEF的面积为k,
∴四边形EFCD的面积为6-k,
∴△MDF的面积=×(k+6),
∵△MEC的面积=△AEB的面积,
∴×(k+6)+6-k=6,
∵k=2,
故选:A.
8.
解:因为二次函数的图像开口向上,得出a>0,与y轴交点在y轴的负半轴,得出c<0,利用对称轴>0,得出b<0,
所以一次函数y=ax+b经过一、三、四象限,反比例函数经过二、四象限.
故选:A.
9.
解:∵反比例函数,当x>0,k>0时,y随x增大而减小
∴,即.
故答案为:.
10.
解:∵
∴该抛物线的顶点坐标为(2,-5).
故答案为(2,-5).
11.
解:,
设
,
故答案为:.
12.
解:观察图象得:该抛物线与轴的一个交点为(-1,0),对称轴为直线,
∴该抛物线与轴的另一个交点坐标是(5,0).
故答案为:(5,0)
13.
解:根据题意,设宽为,
∴,解方程得,,
∵,
∴,
故答案是:.
14.
时,,时,,则方程的根在之间,
而当时,更接近于0,
原方程的一个近似解为
故答案为:1.7.
15.
解:∵二次函数,
∴该函数的对称轴是直线x=2,函数图象开口向下,当x=2时,取得最大值9,
当x=8时y=﹣27,
∴当﹣3≤x≤8时,y的取值范围是﹣27≤y≤9,
故答案为:﹣27≤y≤9.
16.
∵四边形ABCD是正方形,
∴∠B=∠C=90°,AB=BC=12,
∴∠BEP+∠EPB=90°,
∵AE=0.25AB,
∴AE=3,
∴BE=AB-AE=9,
设BP=x,则CP=BC-BP=12-x,
∵PQ⊥EP,
∴∠EPQ=90°,
∴∠EPB+∠QPC=90°,
∴∠BEP=∠QPC,
∴△BPE∽△CQP,
∴,
∴,
∴,
∴当x=6时,CQ的最大值为4,
故答案为4.
17.
解:(1)∵二次函数y=x2-2mx+5m的图象经过点(1,-2),
∴-2=1-2m+5m,
解得;
∴二次函数的表达式为y=x2+2x-5.
(2)二次函数图象的对称轴为直线;
故二次函数的对称轴为:直线;
18. (1)
解:当时,,
∵,
∴此函数的图象与轴有一个交点;
(2)
证明:∵,,,
∴.
∵,
∴,
故不论取何值,函数的图象与轴总有公共点.
19. (1)
证明:∵∠BAD=∠C,∠B=∠B,
∴△ABD∽△CBA;
(2)
解:设DC=x,
∵△ABD∽△CBA,
∴,
∴,
解得,x=12;
即CD=12.
20. (1)
解:∵反比例函数y的图象经过点A(﹣3,2),
∴m=﹣3×2=﹣6,
∵点B(1,n)在反比例函数图象上,
∴n=﹣6.
∴B(1,﹣6),
把A,B的坐标代入y=kx+b,则,
解得k=﹣2,b=﹣4,
∴一次函数的解析式为y=﹣2x﹣4,反比例函数的解析式为y;
(2)
解:如图,设直线AB交y轴于C,
则C(0,﹣4),
∴S△AOB=S△OCA+S△OCB4×34×1=8;
(3)
解:观察函数图象知,
不等式kx+b的解集为x<﹣3或0<x<1.
21. (1)
解:设y与t之间的函数表达式为,
把点(2,120)代入得:
,解得:k=240,
∴y与t之间的函数表达式为;
(2)
解:当t=6时,,
∵k=240>0,
∴y随t的增大而减小,
∴当时,,
答:平均每天至少要卸货40吨.
22. (1)
解:设现在实际购进这种牛肉每千克a元,则原来购进这种牛肉每千克(a+2)元,由题意得:32(a+2)=33a,
解得:a=64(元),
答:现在实际购进这种牛肉每千克64元;
(2)
解:设利润为W,依题意得:
,
∵,
∴W有最大值,
∴当时,(元).
答:这批牛肉的销售单价定为74时,能获得最大利润,最大利润是1000元.
23.
解:当△PBQ∽△ABC时,
,
即,
解得,
经检验:是方程的解,
当△PBQ∽△CBA时,
,
即,
解得,
经检验:是方程的解,
∴的值是或.
24. (1)
解:把代入抛物线,解得,
∴抛物线解析式为 ,
把,两点代入一次函数,
得,解得,
∴一次函数的解析式为,
由图像得,关于x的不等式的解集是或
(2)
解:如图:过点A作y轴的平行线,过点B作x轴的平行线,两者交于点C,连接PC,
∵,
∴,,
设P点的坐标为m,则点P的纵坐标为,
如图,过点P作PD⊥AC延长线于点D,作PE⊥BC于点E,
则
∴ ,
∴
=
=
=,
∵.
∴当m=﹣=时,有最大值,
∴当m=时,=﹣,
∴面积最大时点P的坐标为.
(3)
解:存在,理由如下:
∵P,Q,A,B为顶点的四边形是平行四边形时,
∴,
∵,,
设P,根据平行四边形对角线中点坐标性质,分情况讨论:
①若该平行四边形的对角线是,则,解得,
把代入,解得,则;
②若该平行四边形的对角线是,则,解得,
把代入,解得,则;
③若该平行四边形的对角线是,则,解得,
把代入,解得,则;
故符合条件的P点坐标为:或或.
25.(1)
(2)
(3) (1)
解:∵四边形是平行四边形,,
∴,点C的纵坐标为4,点B到y轴的距离为10,
∴点C的横坐标为3,
∴点C的坐标为,
设直线解析式为,
∴,解得:,
∴直线解析式为;
(2)
解:如图,过C作于点D,
∵点C的坐标为,
∴,
∴,
∴当时,点Q到达点B处,当时,点E到达点C处,当时,点Q到达点C处,
根据题意得:,
当时,点E在上,点Q在上,
∵轴,
∴,
∴,
∴,即,解得:,
过点Q作轴于点M,则,
∵,
∴
∴,
∴,即,
∴,
∴,
∴;
当时,点E在上,点Q在上,过点Q作轴于点F,
根据题意:,
∴,
∴,
∴;
当点E与点Q相遇时,,解得:,
当时,如图,
,
∴;
当时,如图,
,
∴;
综上所述,S关于t的函数解析式为;
(3)
解:能,理由如下:
根据题意得:点P的坐标为,
当时,由(2)得:点Q的坐标为,点E的坐标为,,
∵,且,
∴,
当时,,解得:(舍去);
当时,,此方程无解;
当时,由(2)得:点Q的坐标为,点E的坐标为,,
∵,且,
∴,
当时,,解得:(舍去)或6(舍去);
当时,,此方程无解;
当时,此时,由(2)得:点Q的坐标为,点E的坐标为,,
当时,,解得:;
当时,此时,由(2)得:点Q的坐标为,点E的坐标为,
当时,,(舍去);
综上所述,当时,为等腰三角形.
姓名:___________班级:_____考号:_____
一、选择题(每题3分,共24分)
1.下列函数中,y是x的二次函数的是 ( )
A. B. C. D.
2.已知,则下列比例式成立的是 ( )
A. B. C. D.
3.将抛物线先向左平移2个单位,再向上平移3个单位后,得到( )
A. B.
C. D.
4.如图,在△ABC中,,若AD∶DB=3∶2,AE=6cm,则AC的长为( )
A.6cm B.5cm C.4cm D.10cm
5.如图,在中,是斜边上的高,若,,则的长为 ( )
A.8 B.10 C.9 D.12
6.在平面直角坐标系中,已知抛物线与关于y轴对称,则的值为 ( )
A.6 B. C. D.
7.如图,四边形的面积为18,,且,E为的中点,的延长线交于F,则的面积是 ( )
A.2 B. C. D.3
8.二次函数y=ax2+bx+c(a≠0)的图像如图所示,则一次函数y=ax+b和反比例函数y=(c≠0)在同一直角坐标系中的图像可能是 ( )
A. B.
C. D.
二、填空题(每题3分,共24分)
9.反比例函数y,当x>0时y随x增大而减小,则m的取值范围是 .
10.抛物线的顶点坐标是__________.
11.已知,那么______.
12.抛物线(为常数)的部分图象如图所示,则该抛物线与轴的另一个交点坐标是_________.
13.已知一本书的宽与长之比为黄金比,且这本书的长是,则它的宽为__________cm.(结果保留整数)
14.下表为二次函数的自变量x与函数值y的部分对应值,可以判定的一个近似解x为_________(精确到0.1).
x 1.3 1.4 1.5 1.6 1.7 1.8 1.9
-0.71 -0.54 -0.35 -0.14 0.09 0.34 0.61
15.已知二次函数,若﹣3≤x≤8,则y的取值范围是 _____.
16.如图,在正方形ABCD中,AB=12,AE=0.25AB,点P在BC上运动(不与点B,C重合),过点P作PQ⊥EP,交CD于点Q,则CQ的最大值为______
三、解答题(每题8分,共72分)
17.在平面直角坐标系中,二次函数的图象经过点.
(1)求二次函数的表达式;
(2)求二次函数图象的对称轴.
18.已知二次函数(m为常数).
(1)当时,此函数的图象与x轴有几个交点?
(2)求证∶不论m为何值,该二次函数的图象与x轴总有公共点.
19.如图,在△ABC中,D为BC上一点,∠BAD=∠C.
(1)求证:△ABD∽△CBA;
(2)若AB=8,BD=4,求CD的长.
20.已知一次函数y=kx+b与反比例函数y的图像交于A(﹣3,2)、B(1,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)结合图像直接写出不等式kx+b的解集.
21.一艘载满货物的轮船到达目的地后开始卸货,平均卸货速度y(吨/天)随卸货天数t(天)的变化而变化.已知y与t是反比例函数关系,图像如图所示.
(1)求y与t之间的函数表达式;
(2)由于遇到紧急情况,要求船上的货物不超过6天卸载完毕,那么平均每天至少要卸货多少吨?
22.某超市购进一批牛肉销售,经过还价,实际价格每千克比原来少2元,发现与原来买这批牛肉32千克的钱,现在可以买33千克:
(1)现在实际购进这批牛肉每千克多少元?
(2)若这批牛肉的销售量y(千克)与销售单价x(元/千克)满足,那么这批牛肉的销售单价定为多少时,能获得最大利润?最大利润是多少?(利润=销售收入-进货金额)
23.如图,在Rt中,,,,点P从点A出发,以1cm/s的速度沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.设点P、Q运动时间为.当与相似时,的值是多少?
24.如图所示,已知抛物线与一次函数y=kx+b的图像相交于 ,两点,点P是抛物线上不与A,B重合的一个动点,点Q是y轴上的一个动点
(1)直接写出抛物线和一次函数的解析式及关于x的不等式的解集;
(2)当点P在直线上方时,求出面积最大时点P的坐标;
(3)是否存在以P,Q,A,B为顶点的四边形是平行四边形?若存在,直接写出P的坐标;若不存在,请说明理由.
25.如图,平面直角坐标系中,四边形是平行四边形,,动点P从O出发向A以每秒1个单位的速度移动,动点Q从A出发沿的路径以每秒2个单位的速度移动,当其中一个点运动到终点时运动停止,过点P作x轴的垂线,交线段或线段于点E,连接,设运动时间为t秒.
(1)求直线解析式;
(2)设的面积为S,求S关于t的函数解析式,并写出定义域;
(3)在运动过程中,能否为等腰三角形?若能,直接写出t的值,若不能,请说明理由.
参考答案:
1.
解:A、是二次函数,故符合题意;
B、是一次函数,故不合题意;
C、含有分式,不是二次函数,故不合题意;
D、含有分式,不是二次函数,故不合题意.
故选:A.
2.
A.变成等积式是:,故不符合题意;
B.变成等积式是:,故符合题意;
C.变成等积式是:,故不符合题意;
D.变成等积式是:,故不符合题意.
故选:B.
3.
解:抛物线向左平移2个单位.再向上平移3个单位,
∴平移后的抛物线解析式为.
故选:A.
4.
解∶∵,AD∶DB=3:2,
∴AD∶DB=AE∶EC=3∶2,
∵AE=6cm,
∴6∶EC=3∶2,
∴EC=4cm,
∴AC=AE+EC=10cm.
故选:D
5.
解:如图所示,
∵,,
∴,,
∴,,
∴,
∴,即,且,,
∴,
故选:.
6.
解:∵,抛物线与关于y轴对称,
∴,
∴,,
∴,
故选:B
7.
解:作辅助线如下:延长EF交CD的延长线于点M,
∵,
∴∠ABE=∠DME, ∠BAE=∠MCE,
∵E为的中点,
∴AE=CE,
∴△ABE△CME,
∴CM=AB.
∵,
∴,
∴CD=MD=,
∴△ADC的面积=×△ABC的面积,
∵E为AC的中点,
∴△AEB的面积=△ECB的面积=×△ABC的面积,
∴△ADC的面积=△AEB的面积=△ECB的面积,
∵四边形的面积为18,
∴△ADC的面积=△AEB的面积=△ECB的面积=×四边形ABCD的面积=×18=6.
∵,
∴∠ABF=∠DMF, ∠BAF=∠MDF,
∴△MDF∽△FAB,
∵MD=AB,
∴△MDF的面积=×△AFB的面积,
∵假设△AEF的面积为k,
∴四边形EFCD的面积为6-k,
∴△MDF的面积=×(k+6),
∵△MEC的面积=△AEB的面积,
∴×(k+6)+6-k=6,
∵k=2,
故选:A.
8.
解:因为二次函数的图像开口向上,得出a>0,与y轴交点在y轴的负半轴,得出c<0,利用对称轴>0,得出b<0,
所以一次函数y=ax+b经过一、三、四象限,反比例函数经过二、四象限.
故选:A.
9.
解:∵反比例函数,当x>0,k>0时,y随x增大而减小
∴,即.
故答案为:.
10.
解:∵
∴该抛物线的顶点坐标为(2,-5).
故答案为(2,-5).
11.
解:,
设
,
故答案为:.
12.
解:观察图象得:该抛物线与轴的一个交点为(-1,0),对称轴为直线,
∴该抛物线与轴的另一个交点坐标是(5,0).
故答案为:(5,0)
13.
解:根据题意,设宽为,
∴,解方程得,,
∵,
∴,
故答案是:.
14.
时,,时,,则方程的根在之间,
而当时,更接近于0,
原方程的一个近似解为
故答案为:1.7.
15.
解:∵二次函数,
∴该函数的对称轴是直线x=2,函数图象开口向下,当x=2时,取得最大值9,
当x=8时y=﹣27,
∴当﹣3≤x≤8时,y的取值范围是﹣27≤y≤9,
故答案为:﹣27≤y≤9.
16.
∵四边形ABCD是正方形,
∴∠B=∠C=90°,AB=BC=12,
∴∠BEP+∠EPB=90°,
∵AE=0.25AB,
∴AE=3,
∴BE=AB-AE=9,
设BP=x,则CP=BC-BP=12-x,
∵PQ⊥EP,
∴∠EPQ=90°,
∴∠EPB+∠QPC=90°,
∴∠BEP=∠QPC,
∴△BPE∽△CQP,
∴,
∴,
∴,
∴当x=6时,CQ的最大值为4,
故答案为4.
17.
解:(1)∵二次函数y=x2-2mx+5m的图象经过点(1,-2),
∴-2=1-2m+5m,
解得;
∴二次函数的表达式为y=x2+2x-5.
(2)二次函数图象的对称轴为直线;
故二次函数的对称轴为:直线;
18. (1)
解:当时,,
∵,
∴此函数的图象与轴有一个交点;
(2)
证明:∵,,,
∴.
∵,
∴,
故不论取何值,函数的图象与轴总有公共点.
19. (1)
证明:∵∠BAD=∠C,∠B=∠B,
∴△ABD∽△CBA;
(2)
解:设DC=x,
∵△ABD∽△CBA,
∴,
∴,
解得,x=12;
即CD=12.
20. (1)
解:∵反比例函数y的图象经过点A(﹣3,2),
∴m=﹣3×2=﹣6,
∵点B(1,n)在反比例函数图象上,
∴n=﹣6.
∴B(1,﹣6),
把A,B的坐标代入y=kx+b,则,
解得k=﹣2,b=﹣4,
∴一次函数的解析式为y=﹣2x﹣4,反比例函数的解析式为y;
(2)
解:如图,设直线AB交y轴于C,
则C(0,﹣4),
∴S△AOB=S△OCA+S△OCB4×34×1=8;
(3)
解:观察函数图象知,
不等式kx+b的解集为x<﹣3或0<x<1.
21. (1)
解:设y与t之间的函数表达式为,
把点(2,120)代入得:
,解得:k=240,
∴y与t之间的函数表达式为;
(2)
解:当t=6时,,
∵k=240>0,
∴y随t的增大而减小,
∴当时,,
答:平均每天至少要卸货40吨.
22. (1)
解:设现在实际购进这种牛肉每千克a元,则原来购进这种牛肉每千克(a+2)元,由题意得:32(a+2)=33a,
解得:a=64(元),
答:现在实际购进这种牛肉每千克64元;
(2)
解:设利润为W,依题意得:
,
∵,
∴W有最大值,
∴当时,(元).
答:这批牛肉的销售单价定为74时,能获得最大利润,最大利润是1000元.
23.
解:当△PBQ∽△ABC时,
,
即,
解得,
经检验:是方程的解,
当△PBQ∽△CBA时,
,
即,
解得,
经检验:是方程的解,
∴的值是或.
24. (1)
解:把代入抛物线,解得,
∴抛物线解析式为 ,
把,两点代入一次函数,
得,解得,
∴一次函数的解析式为,
由图像得,关于x的不等式的解集是或
(2)
解:如图:过点A作y轴的平行线,过点B作x轴的平行线,两者交于点C,连接PC,
∵,
∴,,
设P点的坐标为m,则点P的纵坐标为,
如图,过点P作PD⊥AC延长线于点D,作PE⊥BC于点E,
则
∴ ,
∴
=
=
=,
∵.
∴当m=﹣=时,有最大值,
∴当m=时,=﹣,
∴面积最大时点P的坐标为.
(3)
解:存在,理由如下:
∵P,Q,A,B为顶点的四边形是平行四边形时,
∴,
∵,,
设P,根据平行四边形对角线中点坐标性质,分情况讨论:
①若该平行四边形的对角线是,则,解得,
把代入,解得,则;
②若该平行四边形的对角线是,则,解得,
把代入,解得,则;
③若该平行四边形的对角线是,则,解得,
把代入,解得,则;
故符合条件的P点坐标为:或或.
25.(1)
(2)
(3) (1)
解:∵四边形是平行四边形,,
∴,点C的纵坐标为4,点B到y轴的距离为10,
∴点C的横坐标为3,
∴点C的坐标为,
设直线解析式为,
∴,解得:,
∴直线解析式为;
(2)
解:如图,过C作于点D,
∵点C的坐标为,
∴,
∴,
∴当时,点Q到达点B处,当时,点E到达点C处,当时,点Q到达点C处,
根据题意得:,
当时,点E在上,点Q在上,
∵轴,
∴,
∴,
∴,即,解得:,
过点Q作轴于点M,则,
∵,
∴
∴,
∴,即,
∴,
∴,
∴;
当时,点E在上,点Q在上,过点Q作轴于点F,
根据题意:,
∴,
∴,
∴;
当点E与点Q相遇时,,解得:,
当时,如图,
,
∴;
当时,如图,
,
∴;
综上所述,S关于t的函数解析式为;
(3)
解:能,理由如下:
根据题意得:点P的坐标为,
当时,由(2)得:点Q的坐标为,点E的坐标为,,
∵,且,
∴,
当时,,解得:(舍去);
当时,,此方程无解;
当时,由(2)得:点Q的坐标为,点E的坐标为,,
∵,且,
∴,
当时,,解得:(舍去)或6(舍去);
当时,,此方程无解;
当时,此时,由(2)得:点Q的坐标为,点E的坐标为,,
当时,,解得:;
当时,此时,由(2)得:点Q的坐标为,点E的坐标为,
当时,,(舍去);
综上所述,当时,为等腰三角形.
同课章节目录
