八年级全等模型第1讲一线三等角 课件(共12张PPT)
文档属性
| 名称 | 八年级全等模型第1讲一线三等角 课件(共12张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 18:49:16 | ||
图片预览




文档简介
(共12张PPT)
八年级全等模型汇总
第1讲 一线三等角
八年级全等模型汇总
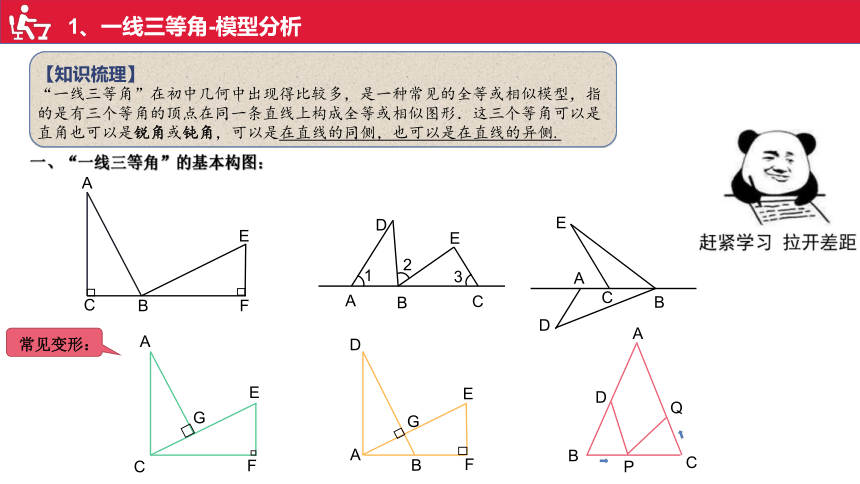
1、一线三等角-模型分析
【知识梳理】
“一线三等角”在初中几何中出现得比较多,是一种常见的全等或相似模型,指的是有三个等角的顶点在同一条直线上构成全等或相似图形.这三个等角可以是直角也可以是锐角或钝角,可以是在直线的同侧,也可以是在直线的异侧.
一、“一线三等角”的基本构图:
A
B
A
C
E
F
A
B
C
D
E
E
D
C
B
1
2
3
常见变形:
C
F
B
F
A
A
G
E
D
A
G
E
B
D
Q
P
C
一线三等角-模型分析
二、“一线三等角”的基本应用:
“一线三等角”主要应用于导角证三角形的全等.
最常见的是直角型“一线三等角”,其次是60°角和45°角及一般的角.
【方法技巧】
用法:若一线三等角都具备则直接应用;若一线三等角不完全具备,则需要构造出一线三等角.
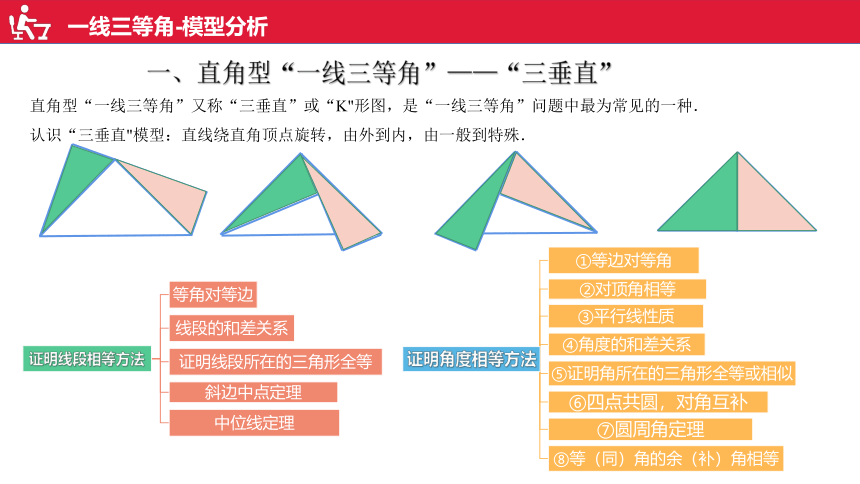
一线三等角-模型分析
一、直角型“一线三等角”——“三垂直”
直角型“一线三等角”又称“三垂直”或“K"形图,是“一线三等角”问题中最为常见的一种.
认识“三垂直"模型:直线绕直角顶点旋转,由外到内,由一般到特殊.
例1、已知:在△ABC中,AB=AC,∠BAC=90° ,过点A作直线l,过B,C分别作BD⊥l于点D,CE⊥l于点E.
(1)如图1,当直线l在△ABC的外部时,求证:DE= BD+CE;
(2)当直线l在△ABC的内部如图2所示时,求证:DE=BD-CE;
(3)当直线l在△ABC的内部如图3所示时,直接写出DE, BD,CE三者之间的数量关系式为____________.
课堂练习
1
2
3
课堂练习
【答案】(1)
∵BD⊥l于点D,CE⊥l于点E.
∴∠BDA=∠CEA=90°
∴∠BAD+∠ABD=180°-∠BDA=90°
∵∠BAC=90°
∴∠BAD+∠CAE=180°-∠BAC=90°
则∠ABD=∠CAE
在Rt△BDA和Rt△AEC中
∴Rt△BDA≌Rt△AEC(AAS)
∴AD=CE,BD=AE
∴BD+CE=AE+AD=DE
(2)∵BD⊥l于点D,CE⊥l于点E.
∴∠BDA=∠CEA=90°
∴∠BAD+∠ABD=180°-∠BDA=90°
∵∠BAC=90°
∴∠BAD+∠CAE=180°-∠BAC=90°
则∠ABD=∠CAE
在Rt△BDA和Rt△AEC中
∴Rt△BDA≌Rt△AEC(AAS)
∴AD=CE,BD=AE
∴BD+CE=AE+AD=DE
(3)CE=BD+DE
【解析】
(1)(2)利用一线三等角的全等模型,利用角度的等量代换,容易证出
Rt△BDA≌Rt△AEC(AAS)
(3)同理,结合上述证明思路,得出对应三角形的全等关系,找到对应边相等即可,再根据线段的和差关系不难解出答案。
课堂练习
二、等边三角形中的“一线三等角”
例1、如图,△ABC为等边三角形,D,E,F分别AB , BC,AC上的点,∠DEF= 60°, BD=CE.求证:BE= CF.
【解答】
已知△ABC为等边三角形
∴∠B=∠C=60°
∴∠BED+∠BDE=120°
∵∠DEF=60°
∴∠BED+∠FEC=120°
∴∠BDE=∠FEC
在△BED和△FCE中
∴△BED≌△FCE(ASA)
∴BE=CF
【分析】本题关键在于求证△BED≌△FCE(ASA)
一线三等角
课堂练习
练习1.如图,△ABC为等边三角形,D,E分别是BC,AC上的点, BE,AD交于点F,∠AFE=60°.求证:AD= BE.
【解答】∵△BAC是等边三角形,∴∠BAC=∠C=60°,AB=AC
∵∠AFE=60°且是△BFA的外角
∴∠BAF +∠FBA =∠AFE=60°.
∵∠BAF+∠DAC=∠BAC=60°
∴∠EBA=∠DAC
在△BAE和△ACD中
∴△BAE≌△ACD(ASA)
∴AD=BE.
【分析】本题属于一线三等角的全等模型,利用角度的和差关系,将∠EBA=∠DAC求证出,进而转化为ASA的全等证明
课堂练习
三、等腰直角三角形中的“一线三等角”
例1、如图,在等腰Rt△ABC中,∠ACB=90°,点D,E分别为AB 、BC上的点,且CD= DE,∠CDE=45°求证:BD= BC.
【解答】已知在等腰Rt△ABC中,∠ACB=90°
∴∠B=45°∵CD= DE,∠CDE=45°
∴∠DCE=
在△DCB中,同理∠CDB=180°-∠DCE-∠B=67.5°
∴∠DCE=∠CDB
∴BD= BC
【分析】利用三角形内角和等于180°定理,再利用角度的和差关系,进而利用等角对等边得到答案
课堂练习
练习1.如图,在四边形ABCD中,∠ADC=∠C=90° , BC=7,AD=4,过点A作AE⊥AB,垂足为A,且AE=AB,连接DE.求△ADE的面积.
构造全等
【解析】
构造Rt△EMA≌Rt△BNA(ASA)
求得EM=BN=7-4=3
∴6
课堂练习
2.已知:在四边形ABCD中,AD//BC,AB=AD,∠ABC=2∠C=2α,点E在AD.上,点 F在DC上.
(1)如图1,若α=45°,∠BDC的度数为
(2)如图2,当α=45°,∠BEF=90°时,求证: EB=EF;
(3)如图3,若α=30°,则当∠BEF= 时,使得EB= EF成立 (请直接写出结果)
90°
构造Rt△EHB≌Rt△EDF(ASA)
120°
在AB上截取AN=AE,进而求证△BNE≌△EDF
作EH//AB,交BD于点H;求证△BHE≌△EDF
课后练习
例1、如图8,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为( )
A.2 B.4 C.5 D.不能确定
例2、已知:在△ABC中,∠BAC=90° ,AB=AC,AE是过点A的一条直线,且BD⊥AE于D,CE⊥AE于E.
(1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由;
(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系如何?请说明理由;
(3)归纳(1)、(2),请用简洁的语言表达BD、DE、CE之间的关系.
B
(1)略(2)BD=DE-CE
(3)当D、E位于直线BC异侧时,BD=DE+CE;
当D、E位于直线BC同侧时,BD=DE-CE.
八年级全等模型汇总
第1讲 一线三等角
八年级全等模型汇总
1、一线三等角-模型分析
【知识梳理】
“一线三等角”在初中几何中出现得比较多,是一种常见的全等或相似模型,指的是有三个等角的顶点在同一条直线上构成全等或相似图形.这三个等角可以是直角也可以是锐角或钝角,可以是在直线的同侧,也可以是在直线的异侧.
一、“一线三等角”的基本构图:
A
B
A
C
E
F
A
B
C
D
E
E
D
C
B
1
2
3
常见变形:
C
F
B
F
A
A
G
E
D
A
G
E
B
D
Q
P
C
一线三等角-模型分析
二、“一线三等角”的基本应用:
“一线三等角”主要应用于导角证三角形的全等.
最常见的是直角型“一线三等角”,其次是60°角和45°角及一般的角.
【方法技巧】
用法:若一线三等角都具备则直接应用;若一线三等角不完全具备,则需要构造出一线三等角.
一线三等角-模型分析
一、直角型“一线三等角”——“三垂直”
直角型“一线三等角”又称“三垂直”或“K"形图,是“一线三等角”问题中最为常见的一种.
认识“三垂直"模型:直线绕直角顶点旋转,由外到内,由一般到特殊.
例1、已知:在△ABC中,AB=AC,∠BAC=90° ,过点A作直线l,过B,C分别作BD⊥l于点D,CE⊥l于点E.
(1)如图1,当直线l在△ABC的外部时,求证:DE= BD+CE;
(2)当直线l在△ABC的内部如图2所示时,求证:DE=BD-CE;
(3)当直线l在△ABC的内部如图3所示时,直接写出DE, BD,CE三者之间的数量关系式为____________.
课堂练习
1
2
3
课堂练习
【答案】(1)
∵BD⊥l于点D,CE⊥l于点E.
∴∠BDA=∠CEA=90°
∴∠BAD+∠ABD=180°-∠BDA=90°
∵∠BAC=90°
∴∠BAD+∠CAE=180°-∠BAC=90°
则∠ABD=∠CAE
在Rt△BDA和Rt△AEC中
∴Rt△BDA≌Rt△AEC(AAS)
∴AD=CE,BD=AE
∴BD+CE=AE+AD=DE
(2)∵BD⊥l于点D,CE⊥l于点E.
∴∠BDA=∠CEA=90°
∴∠BAD+∠ABD=180°-∠BDA=90°
∵∠BAC=90°
∴∠BAD+∠CAE=180°-∠BAC=90°
则∠ABD=∠CAE
在Rt△BDA和Rt△AEC中
∴Rt△BDA≌Rt△AEC(AAS)
∴AD=CE,BD=AE
∴BD+CE=AE+AD=DE
(3)CE=BD+DE
【解析】
(1)(2)利用一线三等角的全等模型,利用角度的等量代换,容易证出
Rt△BDA≌Rt△AEC(AAS)
(3)同理,结合上述证明思路,得出对应三角形的全等关系,找到对应边相等即可,再根据线段的和差关系不难解出答案。
课堂练习
二、等边三角形中的“一线三等角”
例1、如图,△ABC为等边三角形,D,E,F分别AB , BC,AC上的点,∠DEF= 60°, BD=CE.求证:BE= CF.
【解答】
已知△ABC为等边三角形
∴∠B=∠C=60°
∴∠BED+∠BDE=120°
∵∠DEF=60°
∴∠BED+∠FEC=120°
∴∠BDE=∠FEC
在△BED和△FCE中
∴△BED≌△FCE(ASA)
∴BE=CF
【分析】本题关键在于求证△BED≌△FCE(ASA)
一线三等角
课堂练习
练习1.如图,△ABC为等边三角形,D,E分别是BC,AC上的点, BE,AD交于点F,∠AFE=60°.求证:AD= BE.
【解答】∵△BAC是等边三角形,∴∠BAC=∠C=60°,AB=AC
∵∠AFE=60°且是△BFA的外角
∴∠BAF +∠FBA =∠AFE=60°.
∵∠BAF+∠DAC=∠BAC=60°
∴∠EBA=∠DAC
在△BAE和△ACD中
∴△BAE≌△ACD(ASA)
∴AD=BE.
【分析】本题属于一线三等角的全等模型,利用角度的和差关系,将∠EBA=∠DAC求证出,进而转化为ASA的全等证明
课堂练习
三、等腰直角三角形中的“一线三等角”
例1、如图,在等腰Rt△ABC中,∠ACB=90°,点D,E分别为AB 、BC上的点,且CD= DE,∠CDE=45°求证:BD= BC.
【解答】已知在等腰Rt△ABC中,∠ACB=90°
∴∠B=45°∵CD= DE,∠CDE=45°
∴∠DCE=
在△DCB中,同理∠CDB=180°-∠DCE-∠B=67.5°
∴∠DCE=∠CDB
∴BD= BC
【分析】利用三角形内角和等于180°定理,再利用角度的和差关系,进而利用等角对等边得到答案
课堂练习
练习1.如图,在四边形ABCD中,∠ADC=∠C=90° , BC=7,AD=4,过点A作AE⊥AB,垂足为A,且AE=AB,连接DE.求△ADE的面积.
构造全等
【解析】
构造Rt△EMA≌Rt△BNA(ASA)
求得EM=BN=7-4=3
∴6
课堂练习
2.已知:在四边形ABCD中,AD//BC,AB=AD,∠ABC=2∠C=2α,点E在AD.上,点 F在DC上.
(1)如图1,若α=45°,∠BDC的度数为
(2)如图2,当α=45°,∠BEF=90°时,求证: EB=EF;
(3)如图3,若α=30°,则当∠BEF= 时,使得EB= EF成立 (请直接写出结果)
90°
构造Rt△EHB≌Rt△EDF(ASA)
120°
在AB上截取AN=AE,进而求证△BNE≌△EDF
作EH//AB,交BD于点H;求证△BHE≌△EDF
课后练习
例1、如图8,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为( )
A.2 B.4 C.5 D.不能确定
例2、已知:在△ABC中,∠BAC=90° ,AB=AC,AE是过点A的一条直线,且BD⊥AE于D,CE⊥AE于E.
(1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由;
(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系如何?请说明理由;
(3)归纳(1)、(2),请用简洁的语言表达BD、DE、CE之间的关系.
B
(1)略(2)BD=DE-CE
(3)当D、E位于直线BC异侧时,BD=DE+CE;
当D、E位于直线BC同侧时,BD=DE-CE.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
