14.3.2.1 利用平方差公式因式分解课件(19张PPT)
文档属性
| 名称 | 14.3.2.1 利用平方差公式因式分解课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 16:58:50 | ||
图片预览






文档简介
(共19张PPT)
14.3.2.1利用平方差公式 因式分解
人教版八年级上册
教学目标
1、会用平方差公式因式分解.
2、熟练应用提公因式、套平方差公式因式分解.
3、体会平方差公式的特点,从而进一步认识数学的严谨性和灵活性,感受观察、分析是获取知识解决问题的关键.
重点:用平方差公式因式分解
难点:把多项式适当变形后套用平方差公式因式分解
新知导入
请根据多项式乘法运算法则计算下列结果:
(1)(x+5)(x-5)=______________
(2)(3x+y)(3x-y)=______________
(3)(3m+2n)(3m-2n)=______________
x2-25
9x2-y2
9m2-4n2
它们的结果有什么共同特征?
尝试将它们的结果分别写成两个因式的积,你发现什么?
(1)x2-25=______________
(2)9x2-y2=______________
(3)9m2-4n2=______________
(x+5)(x-5)
(3x+y)(3x-y)
(3m+2n)(3m-2n)
新知讲解
利用平方差公式分解因式
知识点1
思考
多项式a2-b2有什么特点?
是两个数的平方差,可以写成(a+b)(a-b)的形式.
你能将它分解因式吗?
a2-b2=(a+b)(a-b)
新知讲解
)
)(
(
b
a
b
a
–
+
=
2
2
b
a
–
)
)(
(
2
2
b
a
b
a
b
a
–
+
=
–
整式乘法
因式分解
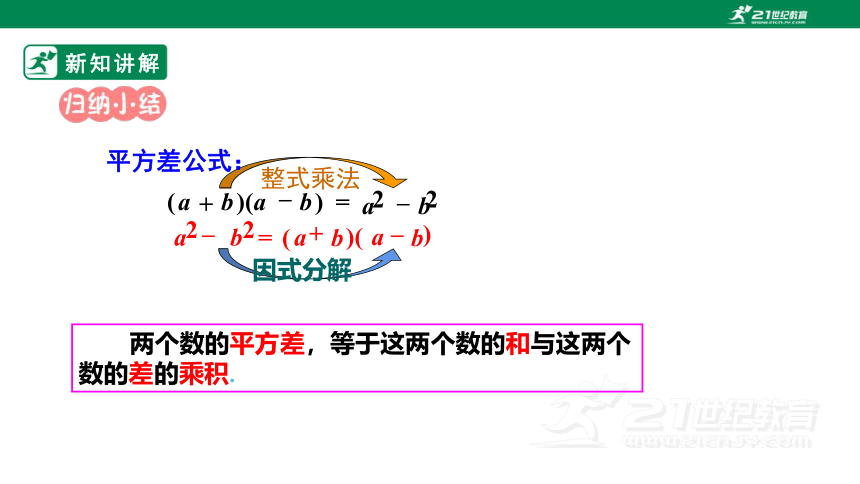
两个数的平方差,等于这两个数的和与这两个数的差的乘积.
平方差公式:
强化练习
下列多项式能否用平方差公式来分解因式?为什么?
(1)
(2)
(3)
(4)
√
√
×
×
【课本P117 练习 第1题】
什么样的多项式可以用平方差公式分解因式?
思考
适用于平方差公式因式分解的多项式必须是二项式,每一项都为平方项,并且两个平方项的符号相反.
例题讲解
分析:在(1)中,4x2-9=( )2-( )2,可用平方差公式来分解因式;在(2)中,令x+p=m,x+q=n,则原式=( )2-( )2.
2x
例1 分解因式:
(1) 4x2-9; (2)(x+p)2-(x+q)2.
3
m
n
整体思想
解:(1)
(2)
例题讲解
分析:对于(1),x4-y4=( )2-( )2,可用平方差公式来分解因式;对于(2),可先提取公因式 ,再用平方差公式来分解因式.
x2
例2 分解因式:
(1) x4-y4; (2) a3b-ab.
y2
ab
解:(1)
(2)
分解完全了吗?
强化练习
(1) (2)
2、分解因式:
=(3a+2b)(3a-2b)
【课本P117 练习 第2题】
(3) (4)
例题讲解
例3 已知x2–y2=–2,x+y=1,求x–y,x,y的值.
∴x–y=–2②.
解:∵x2–y2=(x+y)(x–y)=–2,
x+y=1①,
联立①②组成二元一次方程组,
解得:
方法总结:在与x2–y2,x±y有关的求代数式或未知数的值的问题中,通常需先因式分解,然后整体代入或联立方程组求值.
例题讲解
例4 求证:当n为整数时,多项式(2n+1)2–(2n–1)2一定能被8整除.
即多项式(2n+1)2–(2n–1)2一定能被8整除.
证明:原式=(2n+1+2n–1)(2n+1–2n+1)=4n 2=8n,
∵n为整数,
∴8n被8整除,
方法总结:解决整除的基本思路就是将代数式化为整式乘积的形式,然后分析能被哪些数或式子整除.
强化练习
3、如图,在半径为 R 的圆形钢板上,挖去半径为 r 的四个小圆,计算当 R = 7.8 cm,r = 1.1 cm 时剩余部分的面积 ( π 取 3.14 ).
【课本P120 第7题】
强化练习
4、 如图,某小区规划在边长为 x m 的正方形场地上,修建两条宽为 2 m 的甬道,其余部分种草,你能用几种方法计算甬道所占的面积?
【课本P120 第8题】
课堂总结
平方差公式分解因式
公式
a2–b2=(a+b)(a–b)
步骤
一提:公因式;
二套:公式;
三查:多项式的因式分解有没有分解到不能再分解为止.
拓展提高
1、若a、b、c 是三角形的三边长,且满足(a+b)2-
(b+c)2=0 ,则此三角形是( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.不能确定
A
解析:∵(a+b)2-(b+c)2=0,
(a+b+b+c) (a+b-b-c)=0,
(a+2b+c) (a-c)=0,
∴ a-c=0,即a=c.
拓展提高
2、已知4m+n=40,2m–3n=5.求(m+2n)2–(3m–n)2的值.
原式= – 40×5= –200.
解:原式=(m+2n+3m – n)(m+2n – 3m+n)
=(4m+n)(3n – 2m)
= –(4m+n)(2m – 3n),
当4m+n=40,2m–3n=5时,
拓展提高
3、(1)992–1能否被100整除吗?
解:(1)因为 992–1=(99+1)(99–1)=100×98,
所以,(2n+1)2–25能被4整除.
(2)n为整数,(2n+1)2–25能否被4整除?
所以992–1能被100整除.
(2)原式=(2n+1+5)(2n+1–5)
=(2n+6)(2n–4)
=2(n+3) ×2(n–2)=4(n+3)(n–2).
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
14.3.2.1利用平方差公式 因式分解
人教版八年级上册
教学目标
1、会用平方差公式因式分解.
2、熟练应用提公因式、套平方差公式因式分解.
3、体会平方差公式的特点,从而进一步认识数学的严谨性和灵活性,感受观察、分析是获取知识解决问题的关键.
重点:用平方差公式因式分解
难点:把多项式适当变形后套用平方差公式因式分解
新知导入
请根据多项式乘法运算法则计算下列结果:
(1)(x+5)(x-5)=______________
(2)(3x+y)(3x-y)=______________
(3)(3m+2n)(3m-2n)=______________
x2-25
9x2-y2
9m2-4n2
它们的结果有什么共同特征?
尝试将它们的结果分别写成两个因式的积,你发现什么?
(1)x2-25=______________
(2)9x2-y2=______________
(3)9m2-4n2=______________
(x+5)(x-5)
(3x+y)(3x-y)
(3m+2n)(3m-2n)
新知讲解
利用平方差公式分解因式
知识点1
思考
多项式a2-b2有什么特点?
是两个数的平方差,可以写成(a+b)(a-b)的形式.
你能将它分解因式吗?
a2-b2=(a+b)(a-b)
新知讲解
)
)(
(
b
a
b
a
–
+
=
2
2
b
a
–
)
)(
(
2
2
b
a
b
a
b
a
–
+
=
–
整式乘法
因式分解
两个数的平方差,等于这两个数的和与这两个数的差的乘积.
平方差公式:
强化练习
下列多项式能否用平方差公式来分解因式?为什么?
(1)
(2)
(3)
(4)
√
√
×
×
【课本P117 练习 第1题】
什么样的多项式可以用平方差公式分解因式?
思考
适用于平方差公式因式分解的多项式必须是二项式,每一项都为平方项,并且两个平方项的符号相反.
例题讲解
分析:在(1)中,4x2-9=( )2-( )2,可用平方差公式来分解因式;在(2)中,令x+p=m,x+q=n,则原式=( )2-( )2.
2x
例1 分解因式:
(1) 4x2-9; (2)(x+p)2-(x+q)2.
3
m
n
整体思想
解:(1)
(2)
例题讲解
分析:对于(1),x4-y4=( )2-( )2,可用平方差公式来分解因式;对于(2),可先提取公因式 ,再用平方差公式来分解因式.
x2
例2 分解因式:
(1) x4-y4; (2) a3b-ab.
y2
ab
解:(1)
(2)
分解完全了吗?
强化练习
(1) (2)
2、分解因式:
=(3a+2b)(3a-2b)
【课本P117 练习 第2题】
(3) (4)
例题讲解
例3 已知x2–y2=–2,x+y=1,求x–y,x,y的值.
∴x–y=–2②.
解:∵x2–y2=(x+y)(x–y)=–2,
x+y=1①,
联立①②组成二元一次方程组,
解得:
方法总结:在与x2–y2,x±y有关的求代数式或未知数的值的问题中,通常需先因式分解,然后整体代入或联立方程组求值.
例题讲解
例4 求证:当n为整数时,多项式(2n+1)2–(2n–1)2一定能被8整除.
即多项式(2n+1)2–(2n–1)2一定能被8整除.
证明:原式=(2n+1+2n–1)(2n+1–2n+1)=4n 2=8n,
∵n为整数,
∴8n被8整除,
方法总结:解决整除的基本思路就是将代数式化为整式乘积的形式,然后分析能被哪些数或式子整除.
强化练习
3、如图,在半径为 R 的圆形钢板上,挖去半径为 r 的四个小圆,计算当 R = 7.8 cm,r = 1.1 cm 时剩余部分的面积 ( π 取 3.14 ).
【课本P120 第7题】
强化练习
4、 如图,某小区规划在边长为 x m 的正方形场地上,修建两条宽为 2 m 的甬道,其余部分种草,你能用几种方法计算甬道所占的面积?
【课本P120 第8题】
课堂总结
平方差公式分解因式
公式
a2–b2=(a+b)(a–b)
步骤
一提:公因式;
二套:公式;
三查:多项式的因式分解有没有分解到不能再分解为止.
拓展提高
1、若a、b、c 是三角形的三边长,且满足(a+b)2-
(b+c)2=0 ,则此三角形是( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.不能确定
A
解析:∵(a+b)2-(b+c)2=0,
(a+b+b+c) (a+b-b-c)=0,
(a+2b+c) (a-c)=0,
∴ a-c=0,即a=c.
拓展提高
2、已知4m+n=40,2m–3n=5.求(m+2n)2–(3m–n)2的值.
原式= – 40×5= –200.
解:原式=(m+2n+3m – n)(m+2n – 3m+n)
=(4m+n)(3n – 2m)
= –(4m+n)(2m – 3n),
当4m+n=40,2m–3n=5时,
拓展提高
3、(1)992–1能否被100整除吗?
解:(1)因为 992–1=(99+1)(99–1)=100×98,
所以,(2n+1)2–25能被4整除.
(2)n为整数,(2n+1)2–25能否被4整除?
所以992–1能被100整除.
(2)原式=(2n+1+5)(2n+1–5)
=(2n+6)(2n–4)
=2(n+3) ×2(n–2)=4(n+3)(n–2).
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
