鲁教版数学六年级上3.2代数式(第2课时) 课件(17张PPT)
文档属性
| 名称 | 鲁教版数学六年级上3.2代数式(第2课时) 课件(17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 689.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 15:48:55 | ||
图片预览





文档简介
(共17张PPT)
第三章 整式及其加减
学习新知
检测反馈
2 代数式(第2课时)
(1)遗传是影响一个人身高的因素之一。国外有学者总结出由父母身高预测子女身高的公式:儿子成年后的身高= ,女儿成年后的身高= ,其中a是父亲的身高,b是母亲的身高,单位是:m。现在你可以预测一下自己的身高了。
问题
(2)你们用同一个公式计算的结果相同吗?为什么?
学 习 新 知
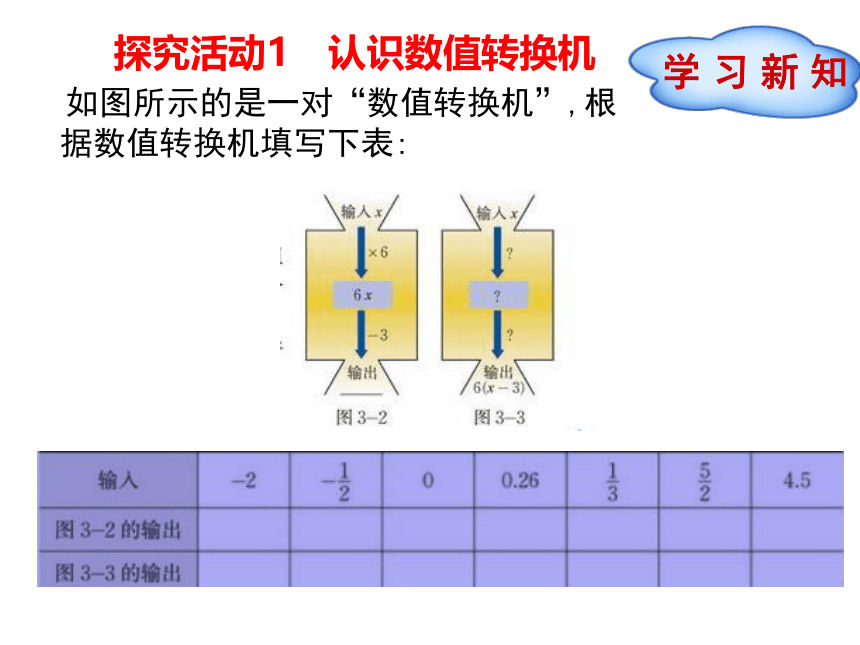
探究活动1 认识数值转换机
如图所示的是一对“数值转换机”,根据数值转换机填写下表:
两次的输出相同吗?为什么?
因为两个数值转换机所表示的代数式不
同,所以输出的结果不相同.
问题
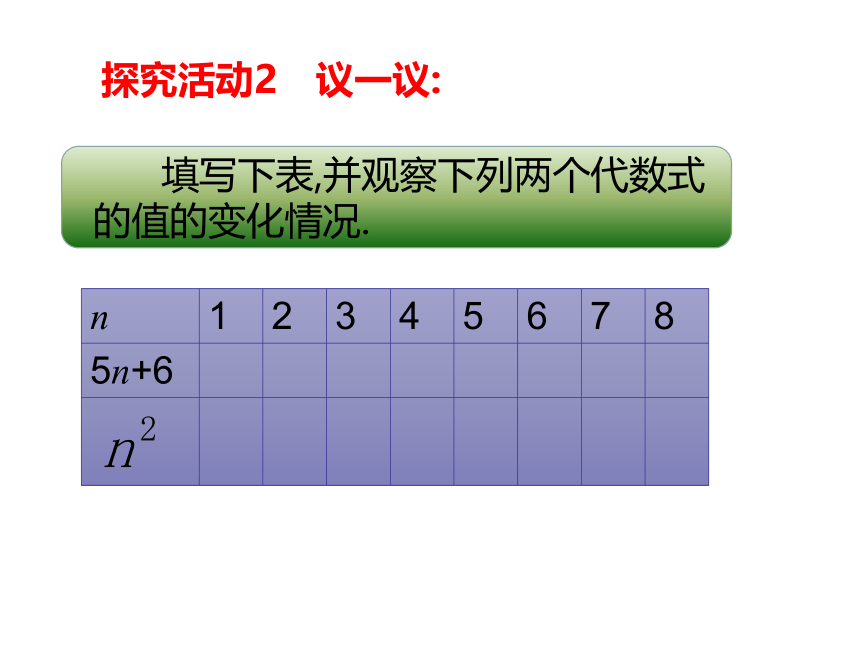
探究活动2 议一议:
填写下表,并观察下列两个代数式的值的变化情况.
n 1 2 3 4 5 6 7 8
5n+6
(1)随着n的值逐渐变大,两个代数式的值如何变化
(2)估计一下,哪个代数式的值先超过100
问题
例1(补充)有一数值转换器,原理如图所示,若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2014次输出的结果是 .
探究活动3 例题解析,应用新知
输入x
x为奇数
x为偶数
x+3
输出
首先由数值转换器发现第二次输出的结果是4,为偶数,所以第三次输出的结果为2,第四次为1,第五次为4,第六次为2,…,可得出规律:从第二次开始,每三次一个循环.因为(2014-1)÷3=671,所以第2014次输出的结果是1.
例2(补充)物体自由下落的高度h m和下落的时间t s的关系,在地球上大约是h=4.9t2,在月球上大约是h=0.8t2.
(1)填写下表:
探究活动4 变式训练,能力提高
t 0 2 4 6 8
10
h=4.9t2
h=0.8t2
(3)当h=20 m时,比较物体在地球上和月球上自由下落所需的时间.
(2)物体在哪儿下落得快
(1)代数式的值是按代数式的运算关系得到的具体数值,随字母取值的不同而不同,字母的值确定了,代数式的值也就确定了,但字母的取值必须确保代数式有意义.
(2)代数式中原来省略乘号时,代入具体数值后出现数与数相乘时,必须恢复乘号.
知识拓展
(3)若做乘方运算,字母给出的数值是负数或分数时,代入时要加括号.
(4)一个代数式的值由它所含字母的值决定,具有不唯一性.
1.代数式求值步骤:
求代数式的值时,先确定是直接代入还是整体代入,然后按照运算顺序进行计算.
2.如何列代数式
列代数式时,要善于抓住关键性的词语,如“大、小、多、少、增加、减少、和、差、积、商”等,还要注意已知量和未知量之间的关系.
知识小结
1.当x=2时,下列代数式中与代数式2x+1的值相等的是 ( )
A.1-x2 B.3x+1
C.3x-x2 D.x2+1
检测反馈
D
解析: 将x=2代入各代数式,得2x+1=5,
1-x2=-3,3x+1=7,3x-x2=2,x2+1=5.故选D.
2.如右图所示的图形的面积用代数式表示是 ( )
A.ab+bc
B.c[b-d+d(a-c)]
C.ad+c(b-d)
D.ab-cd
解析:把图形看成一个大的长方形,面积为ab,再减去长为d,宽为c的长方形的面积,剩下的就是所求图形的面积,即ab-cd.故选D.
D
3.当m=3,n=-2时,代数式m2-2n2的值是 .
解析: 将m=3,n=-2代入m2-2n2得9-2×(-2)2=1.故填1.
4.若x2-2x+1=0,则2x2-4x= .
解析: 根据已知条件目前还解
不出x的值,所以把x2-2x+1=0进行
整体思考,将x2-2x+1=0变形为x2-2x
=-1,2x2-4x=2(x2-2x)=2×(-1)=-2,所以求得2x2-4x=-2.故填-2.
5.代数式x2+x+3的值为7,则代数式
2x2+2x-3的值为 .
解析: 由x2+x+3=7可知x2+x=4,所以2x2+2x-3=2(x2+x)-3
=2×4-3=5.故填5.
第三章 整式及其加减
学习新知
检测反馈
2 代数式(第2课时)
(1)遗传是影响一个人身高的因素之一。国外有学者总结出由父母身高预测子女身高的公式:儿子成年后的身高= ,女儿成年后的身高= ,其中a是父亲的身高,b是母亲的身高,单位是:m。现在你可以预测一下自己的身高了。
问题
(2)你们用同一个公式计算的结果相同吗?为什么?
学 习 新 知
探究活动1 认识数值转换机
如图所示的是一对“数值转换机”,根据数值转换机填写下表:
两次的输出相同吗?为什么?
因为两个数值转换机所表示的代数式不
同,所以输出的结果不相同.
问题
探究活动2 议一议:
填写下表,并观察下列两个代数式的值的变化情况.
n 1 2 3 4 5 6 7 8
5n+6
(1)随着n的值逐渐变大,两个代数式的值如何变化
(2)估计一下,哪个代数式的值先超过100
问题
例1(补充)有一数值转换器,原理如图所示,若开始输入x的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2014次输出的结果是 .
探究活动3 例题解析,应用新知
输入x
x为奇数
x为偶数
x+3
输出
首先由数值转换器发现第二次输出的结果是4,为偶数,所以第三次输出的结果为2,第四次为1,第五次为4,第六次为2,…,可得出规律:从第二次开始,每三次一个循环.因为(2014-1)÷3=671,所以第2014次输出的结果是1.
例2(补充)物体自由下落的高度h m和下落的时间t s的关系,在地球上大约是h=4.9t2,在月球上大约是h=0.8t2.
(1)填写下表:
探究活动4 变式训练,能力提高
t 0 2 4 6 8
10
h=4.9t2
h=0.8t2
(3)当h=20 m时,比较物体在地球上和月球上自由下落所需的时间.
(2)物体在哪儿下落得快
(1)代数式的值是按代数式的运算关系得到的具体数值,随字母取值的不同而不同,字母的值确定了,代数式的值也就确定了,但字母的取值必须确保代数式有意义.
(2)代数式中原来省略乘号时,代入具体数值后出现数与数相乘时,必须恢复乘号.
知识拓展
(3)若做乘方运算,字母给出的数值是负数或分数时,代入时要加括号.
(4)一个代数式的值由它所含字母的值决定,具有不唯一性.
1.代数式求值步骤:
求代数式的值时,先确定是直接代入还是整体代入,然后按照运算顺序进行计算.
2.如何列代数式
列代数式时,要善于抓住关键性的词语,如“大、小、多、少、增加、减少、和、差、积、商”等,还要注意已知量和未知量之间的关系.
知识小结
1.当x=2时,下列代数式中与代数式2x+1的值相等的是 ( )
A.1-x2 B.3x+1
C.3x-x2 D.x2+1
检测反馈
D
解析: 将x=2代入各代数式,得2x+1=5,
1-x2=-3,3x+1=7,3x-x2=2,x2+1=5.故选D.
2.如右图所示的图形的面积用代数式表示是 ( )
A.ab+bc
B.c[b-d+d(a-c)]
C.ad+c(b-d)
D.ab-cd
解析:把图形看成一个大的长方形,面积为ab,再减去长为d,宽为c的长方形的面积,剩下的就是所求图形的面积,即ab-cd.故选D.
D
3.当m=3,n=-2时,代数式m2-2n2的值是 .
解析: 将m=3,n=-2代入m2-2n2得9-2×(-2)2=1.故填1.
4.若x2-2x+1=0,则2x2-4x= .
解析: 根据已知条件目前还解
不出x的值,所以把x2-2x+1=0进行
整体思考,将x2-2x+1=0变形为x2-2x
=-1,2x2-4x=2(x2-2x)=2×(-1)=-2,所以求得2x2-4x=-2.故填-2.
5.代数式x2+x+3的值为7,则代数式
2x2+2x-3的值为 .
解析: 由x2+x+3=7可知x2+x=4,所以2x2+2x-3=2(x2+x)-3
=2×4-3=5.故填5.
