4.2 正切 课件(共45张PPT)

(共45张PPT)
第四章 锐角三角函数
4.2 正 切
1.理解锐角的三角函数中正切的概念及其与现实生活的联系；（重点）
2.能在直角三角形中求出某个锐角的正切值，并进行简单计算； (重点)
学习目标
智者乐水，仁者乐山
图片欣赏
思考：衡量山“险”与“不险”的标准是什么呢？
陡
陡意味着倾斜程度大！
想一想:你能比较两个梯子哪个更陡吗？你有哪些办法？
铅直高度
水平宽度
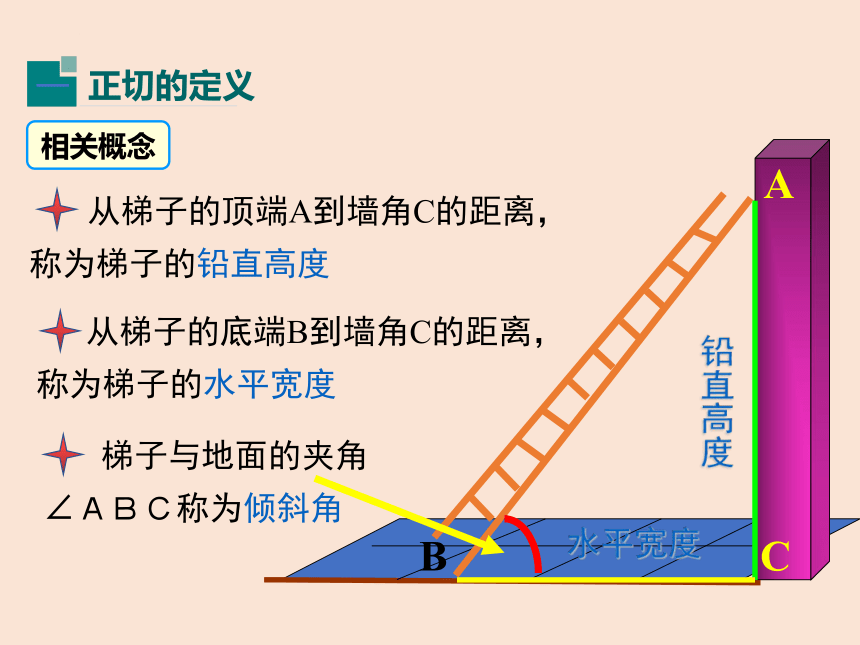
梯子与地面的夹角∠ＡＢＣ称为倾斜角
从梯子的顶端A到墙角C的距离，称为梯子的铅直高度
从梯子的底端B到墙角C的距离，称为梯子的水平宽度
A
C
B
正切的定义
一
相关概念
问题1:你能比较两个梯子哪个更陡吗？你有哪些办法？
合作探究1
A
B
C
D
E
F
倾斜角越大——梯子越陡
问题2:如图，梯子AB和EF哪个更陡？你是怎样判断的？
当铅直高度一样，水平宽度越小，梯子越陡
当水平宽度一样，铅直高度越大，梯子越陡
甲
乙
问题3:如图，梯子AB和EF哪个更陡？你是怎样判断的？
当铅直高度与水平宽度的比相等时，
梯子一样陡
3m
6m
D
E
F
C
2m
B
4m
A
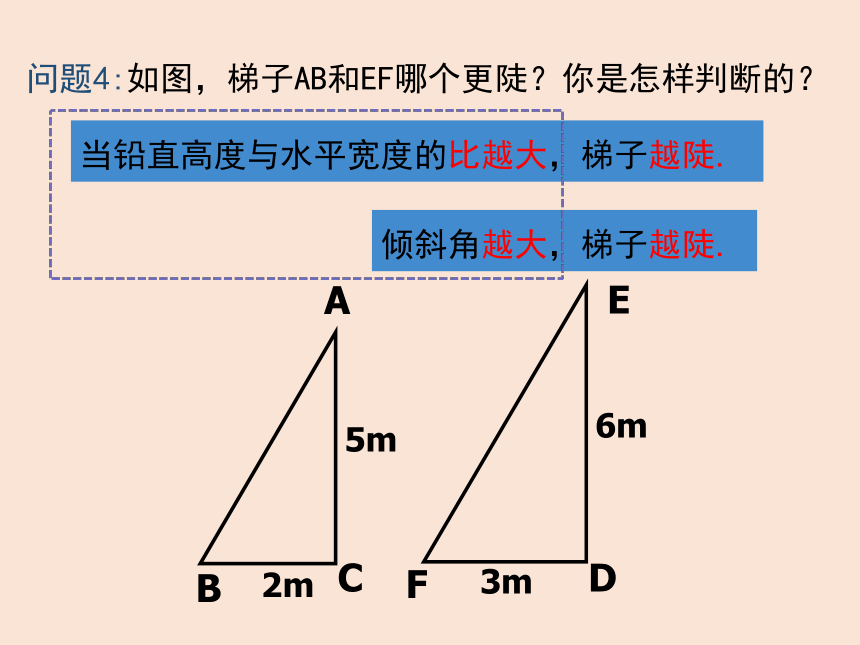
问题4:如图，梯子AB和EF哪个更陡？你是怎样判断的？
当铅直高度与水平宽度的比越大，梯子越陡.
3m
2m
6m
5m
A
B
C
D
E
F
倾斜角越大，梯子越陡.
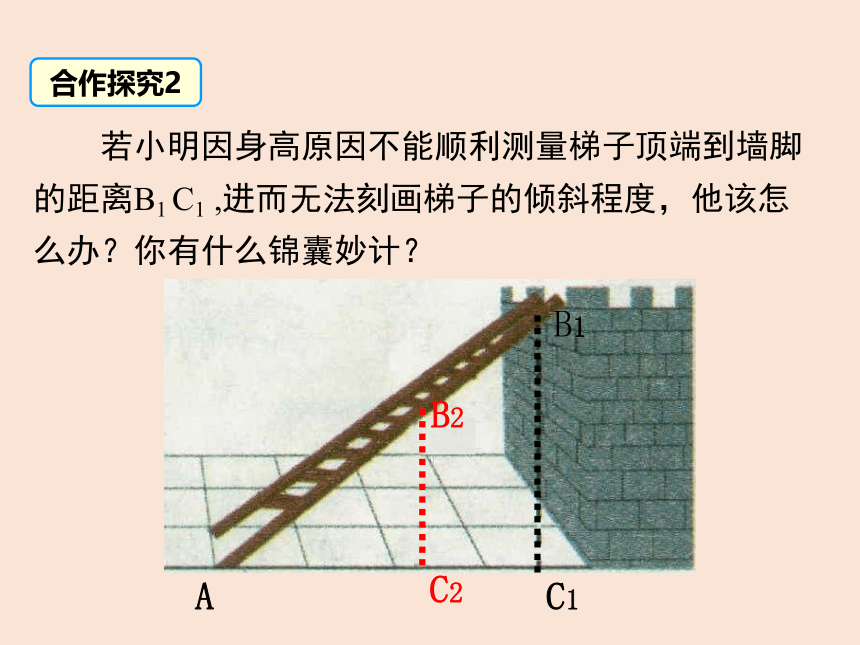
若小明因身高原因不能顺利测量梯子顶端到墙脚的距离B1 C1 ,进而无法刻画梯子的倾斜程度，他该怎么办？你有什么锦囊妙计？
A
C1
C2
B2
B1
合作探究2
两个直角三角形相似
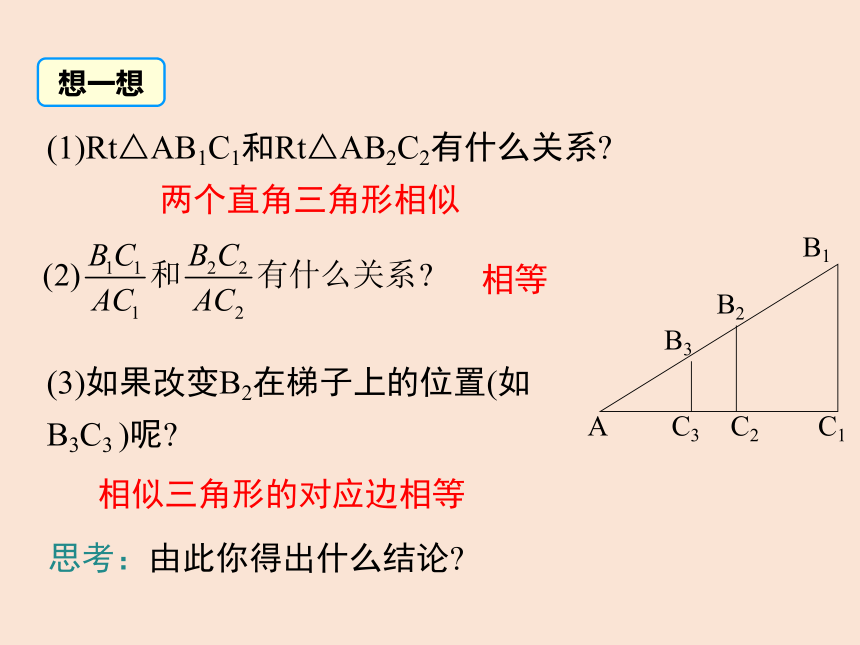
(1)Rt△AB1C1和Rt△AB2C2有什么关系
(3)如果改变B2在梯子上的位置(如B3C3 )呢
思考：由此你得出什么结论
A
B1
C2
C1
B2
C3
B3
想一想
相等
相似三角形的对应边相等
在Rt△ABC中,如果锐角A确定，那么∠A的对边与邻边的比便随之确定，这个比叫做∠A的正切,记作tanA,即
A
B
C
∠A的对边
∠A的邻边
┌
tanA=
归纳总结
结论：tanA的值越大，梯子越陡.
定义中的几点说明：
1.初中阶段，正切是在直角三角形中定义的， ∠A是一个锐角.
2.tanA是一个完整的符号，它表示∠A的正切.但∠BAC的正切表示为:tan∠BAC.∠1的正切表示为:tan∠1.
3.tanA﹥0 且没有单位，它表示一个比值，即直角三角形中锐角∠A的对边与邻边的比（注意顺序： ）.
4.tanA不表示“tan”乘以“A ”.
5.tanA的大小只与∠A的大小有关，而与直角三角形的边长无关.
A
B
C
┌
锐角A的正切值可以等于1吗？为什么？可以大于1吗？
对于锐角A的每一个确定的值，tanA都有唯一的确定的值与它对应.
解：可以等于1，此时为等腰直角三角形；也可以大于1，甚至可逼近于无穷大.
议一议
例1： 下图表示两个自动扶梯,哪一个自动扶梯比较陡
解:甲梯中,
β
6m
┐
乙
8m
α
5m
┌
甲
13m
乙梯中,
∵tanβ＞tanα,∴乙梯更陡.
提示:在生活中,常用一个锐角的正切表示梯子的倾斜程度.
典例精析
例2： 计算：tan45°+tan230°+tan230°tan260°
原式=
1. 在Rt△ABC中，∠C=90°，AC=7，BC=5，则 tan A=______，tan B =______．
练一练
互余两锐角的正切值互为倒数.
2.下图中∠ACB=90°，CD⊥AB,垂足为D.指出∠A和∠B的对边、邻边.
A
B
C
D
(1) tanA =
=
AC
( )
CD
( )
(2) tanB=
=
BC
( )
CD
( )
BC
AD
BD
AC
4.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值（ ）
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定
A
B
C
┌
C
3.已知∠A,∠B为锐角，
(1)若∠A=∠B,则tanA tanB;
(2)若tanA=tanB,则∠A ∠B.
=
=
求 tan30°，tan60°的值.
从而　AC2=AB2-BC2=(2BC)2-BC2=3BC2.
解：
如图，构造一个Rt△ABC，使∠C=90°，∠A=30°，
于是 BC = AB ， ∠B=60°.
由此得出 AC = BC.
因此 　
因此
合作探究
说一说tan 45°的值
tan45°=1
30°、45°、60°角的正弦值、余弦值和正切值如下表：
锐角a 三角 函数 30° 45° 60°
sin a
cos a
tan a
归纳：
1
　　对于一般锐角α（30°，45°，60°除外）的正切值，
我们也可用计算器来求.
用计算器求锐角的正切值或根据正切值求角
二
　　例如求25°角的正切值，可以在计算器上依次按键 　　　　 ，显示结果为0.4663…　　
　　如果已知正切值，我们也可以利用计算
器求出它的对应锐角.
　　例如，已知tanα=0.8391，依次按键
，显示结果为
40.000…，表示角α约等于40°.
总结归纳
从正弦、余弦、正切的定义看到，任意给定一个锐角α，都有唯一确定的比值sinα(或cosα，tanα)与它对应，并且我们还知道，当锐角α变化时，它的比值sinα (或cosα，tanα)也随之变化. 因此我们把锐角α的正弦、余弦和正切统称为角α的锐角三角函数.
定义中应该注意的几个问题:
1.sinA,cosA,tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA是一个完整的符号,分别表示∠A的正弦,余弦,正切 (习惯省去“∠”号).
3.sinA,cosA,tanA 是一个比值.注意比的顺序.且sinA,cosA,tanA均﹥0,无单位.
4.sinA,cosA,tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则其三角函数值相等；两锐角的三角函数值相等,则这两个锐角相等.
例2 求下列各式的值：
提示：cos260°表示(cos60°)2，即
(cos60°)×(cos60°).
解：cos260°+sin260°
典例精析
(1) cos260°+sin260°；
(2)
解：
练一练
计算：
(1) sin30°+ cos45°；
解：原式 =
(2) sin230°+ cos230°－tan45°.
解：原式 =
例3 已知 △ABC 中的 ∠A 与 ∠B 满足 (1－tanA)2 ＋|sinB－ |＝0，试判断 △ABC 的形状．
解：∵ (1－tanA)2 ＋ | sinB－ |＝0，
∴ tanA＝1，sinB＝
∴ ∠A＝45°，∠B＝60°，
∠C＝180°－45°－60°＝75°，
∴ △ABC 是锐角三角形．
练一练
1. 已知：| tanB－ | ＋ (2 sinA－ )2 ＝0，求∠A，∠B的度数.
解：∵ | tanB－ | ＋ (2 sinA－ )2 ＝0，
∴ tanB＝ ，sinA＝
∴ ∠B＝60°，∠A＝60°.
2. 已知 α 为锐角，且 tanα 是方程 x2 + 2x －3 = 0 的一
个根，求 2 sin2α + cos2α － tan (α+15°)的值．
解：解方程 x2 + 2x － 3 = 0，得 x1 = 1，x2 = －3.
∵ tanα ＞0，∴ tanα =1，∴ α = 45°.
∴ 2 sin2α + cos2α － tan (α+15°)
= 2 sin245°+cos245°－ tan60°
B
C
A
(1)在Rt△ABC中∠C=90°，BC=5,
AC=12,tanA=( ).
(2)在Rt△ABC中∠C=90°，BC=5,
AB=13,tanA=( ),tanB=( ).
(3)在Rt△ABC中∠C=90°，BC=5,tanA= ,
AC=( ).
1.完成下列填空：
2.如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tanA= （ ）
A. B.
C. D.
D
这个图呢？
C
A
B
C
A
B
3.如图,P是 的边 OA 上一点，点 P的坐标为
，则 =__________.
M
记得构造直角三角形哦！
O
P(12,5)
A
x
y
5.在等腰△ABC中, AB=AC=13, BC=10,求tanB.
提示:过点A作AD垂直于BC于点D.
求锐角三角函数时,勾股定理的运用是很重要的.
A
C
B
┌
D
解：如图，过点A作AD⊥BC于点D，
∴在Rt△ABD中，
易知BD=5，AD=12.
6.在Rt△ABC中,∠C=90°, AB=15,tanA= ,求AC和BC.
4k
┌
A
C
B
15
3k
7. 如图，在Rt△ABC中，∠C＝90°，AB =10，BC＝6，求sinA、cosA、tanA的值．
解：∵
又∵
A
B
C
6
10
变式1：如图，在Rt△ABC中，∠C＝90°，
cosA＝ ，求sinA、tanA的值．
解：∵
A
B
C
设AC=15k，则AB=17k
所以
∴
变式2：如图，在Rt△ABC中，∠C＝90°，AC＝8，tanA＝ ，求sinA、cosB的值．
A
B
C
8
解：∵
如图，在平面直角坐标系中，P(x,y)是第一象限内直线y=-x+6上的点, 点A(5,0)，O是坐标原点，△PAO 的面积为S.
（1）求S与x的函数关系式；
（2）当S=10时,求tan∠PAO 的值.
M
能力提升
解：(1)过点P作PM⊥OA于点M，
（2）当S=10时,求tan∠PAO 的值.
M
解：
又∵点P在直线y=-x+6上，
∴x=2.
∴AM=OA-OM=5-2=3.
正切
正切的概念：在直角三角形中，锐角α的对边与邻边的比叫做角α的正切
正弦的性质：α确定的情况下，tanα为定值，与三角形的大小无关
用计算器解决正切问题
正切
定义
∠A越大，tanA越大,
梯子越陡
与梯子倾斜程度的关系
谢谢观看