第14章 整式的乘法与因式分解 章末复习课件(21张PPT)
文档属性
| 名称 | 第14章 整式的乘法与因式分解 章末复习课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-23 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
第14章 整式的乘法与因式分解
章末复习课件
人教版八年级上册
教学目标
1. 熟记整式的乘除法法则,正确运用乘法公式.
2. 会将多项式进行因式分解.
3. 能说出整式乘法与因式分解的联系与区别.
复习回顾
要点1 幂的运算性质
字母表达式
同底数幂的乘法
幂的乘方
积的乘方
同底数幂的除法
am·an=am+n
(am)n=amn
(ab)n=anbn
am ÷ an=am-n
复习回顾
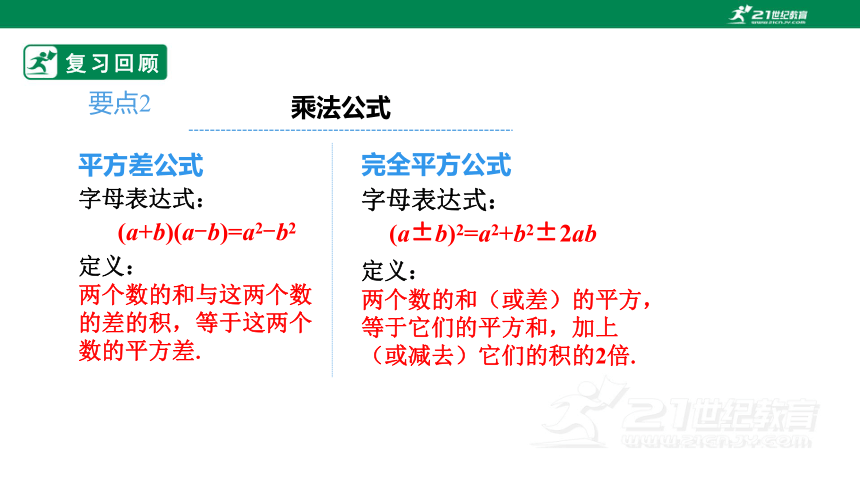
要点2
乘法公式
平方差公式
字母表达式:
定义:
两个数的和与这两个数的差的积,等于这两个数的平方差.
完全平方公式
字母表达式:
定义:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
(a+b)(a-b)=a2-b2
(a±b)2=a2+b2±2ab
复习回顾
要点3 因式分解
定义 把一个多项式化成几个整式的积的形式,这样的式子变形叫做把这个多项式的因式分解,也叫做把这个多项式分解因式.
复习回顾
因式分解的常用方法
1
2
提公因式法
平方差公式
3
完全平方公式
pa+pb+pc=p(a+b+c)
a2-b2=(a+b)(a-b)
(a+b)2=a2+b2+2ab (a-b)2=a2+b2-2ab
复习回顾
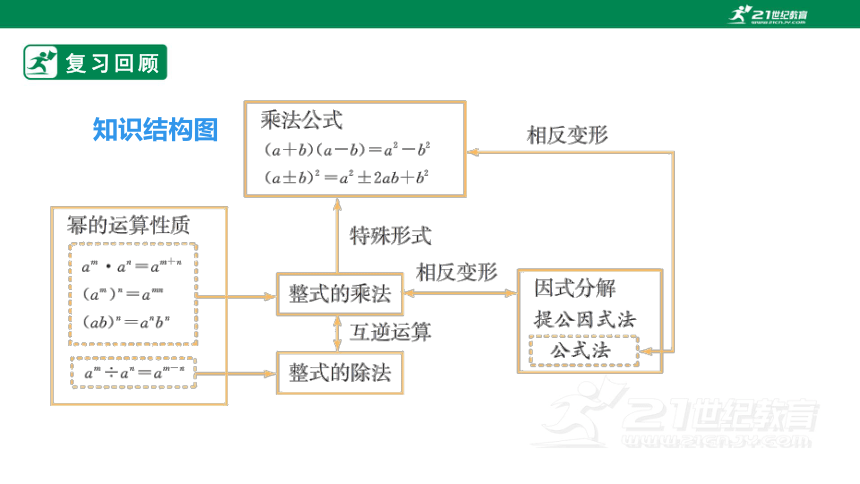
知识结构图
典例讲解
例1 下列运算正确的是( )
A.a2·a3=a6 B.(a4)3=a12
C.(-2ab)3=-6a3b3 D.a4+a5=a9
解析 a2·a3=a2+3=a5,A选项错误;(a4)3=a4×3=a12,B选项正确;(-2ab)3=(-2)3a3b3=-8a3b3,C选项错误;a4和a5不是同类项,不能合并,D选项错误.
B
典例讲解
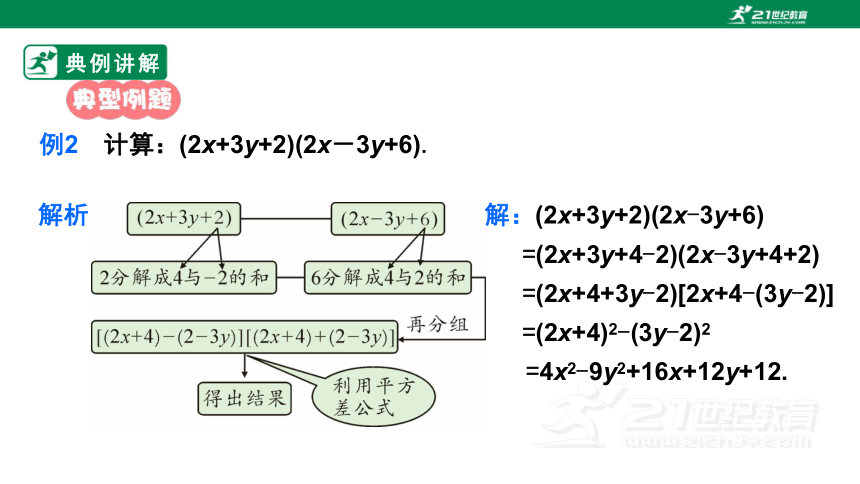
例2 计算:(2x+3y+2)(2x-3y+6).
解析
解:(2x+3y+2)(2x-3y+6)
=(2x+3y+4-2)(2x-3y+4+2)
=(2x+4+3y-2)[2x+4-(3y-2)]
=(2x+4)2-(3y-2)2
=4x2-9y2+16x+12y+12.
强化练习
1. 计算:
(1)4(x+1)2-(2x+5)(2x-5); (2)2x( x2-1)-3x( x2+ );
教材124页第6题
强化练习
1. 计算:
(3)3(y-z)2-(2y+z)(-z+2y); (4)[x(x2y2-xy)-y(x2-x3y)]÷3x2y.
典例讲解
例3 分解因式:
(1)16a4-8a2b2+b4;(2)(x2+3x)2-(x-1)2.
解析 综合运用完全平方公式和平方差公式.注意分解要完全.
解:16a4-8a2b2+b4
=(4a2-b2)2
=(2a+b)2(2a-b)2
解:(x2+3x)2-(x-1)2
=(x2+3x+x-1)(x2+3x-x+1)
=(x2+4x-1)(x+1)2
强化练习
2 .分解因式:
(1)25x2-16y2; (2)(a-b)(x-y)-(b-a)(x+y);
教材124页第3题
强化练习
(3)a2-4ab+4b2; (4)4+12(x-y)+9(x-y)2.
强化练习
3. 已知 (x+y)2 = 25,(x-y)2 = 9,求 xy与 2 + y 的值.
教材125页第8题
强化练习
4. 求证: 当 n 是整数时,两个连续奇数的平方差(2n+1)2-(2n-1)2 是 8 的倍数.
教材125页第11题
典例讲解
例4 如图,水压机有四根空心钢立柱,每根高都是 18 m,外径 D 为 1 m 内径 d 为 0.4 m,每立方米钢的质量为7.8 t,求 4 根立柱的总质量 (π取3.14)
强化练习
5.某种产品的原料提价,因而厂家决定对产品进行提价,
现有三种方案:
(1)第一次提价 p%,第二次提价 q%;
(2)第一次提价 q%,第二次提价 p%;
(3)第一、二次提价均为
其中 p,q 是不相等的正数. 三种方案哪种提价最多?
(提示: 因为 p≠q,(p-q)2 = p2-2pq+q2>0,所以p2+q2 >2pq.)
教材125页第12题
强化练习
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第14章 整式的乘法与因式分解
章末复习课件
人教版八年级上册
教学目标
1. 熟记整式的乘除法法则,正确运用乘法公式.
2. 会将多项式进行因式分解.
3. 能说出整式乘法与因式分解的联系与区别.
复习回顾
要点1 幂的运算性质
字母表达式
同底数幂的乘法
幂的乘方
积的乘方
同底数幂的除法
am·an=am+n
(am)n=amn
(ab)n=anbn
am ÷ an=am-n
复习回顾
要点2
乘法公式
平方差公式
字母表达式:
定义:
两个数的和与这两个数的差的积,等于这两个数的平方差.
完全平方公式
字母表达式:
定义:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
(a+b)(a-b)=a2-b2
(a±b)2=a2+b2±2ab
复习回顾
要点3 因式分解
定义 把一个多项式化成几个整式的积的形式,这样的式子变形叫做把这个多项式的因式分解,也叫做把这个多项式分解因式.
复习回顾
因式分解的常用方法
1
2
提公因式法
平方差公式
3
完全平方公式
pa+pb+pc=p(a+b+c)
a2-b2=(a+b)(a-b)
(a+b)2=a2+b2+2ab (a-b)2=a2+b2-2ab
复习回顾
知识结构图
典例讲解
例1 下列运算正确的是( )
A.a2·a3=a6 B.(a4)3=a12
C.(-2ab)3=-6a3b3 D.a4+a5=a9
解析 a2·a3=a2+3=a5,A选项错误;(a4)3=a4×3=a12,B选项正确;(-2ab)3=(-2)3a3b3=-8a3b3,C选项错误;a4和a5不是同类项,不能合并,D选项错误.
B
典例讲解
例2 计算:(2x+3y+2)(2x-3y+6).
解析
解:(2x+3y+2)(2x-3y+6)
=(2x+3y+4-2)(2x-3y+4+2)
=(2x+4+3y-2)[2x+4-(3y-2)]
=(2x+4)2-(3y-2)2
=4x2-9y2+16x+12y+12.
强化练习
1. 计算:
(1)4(x+1)2-(2x+5)(2x-5); (2)2x( x2-1)-3x( x2+ );
教材124页第6题
强化练习
1. 计算:
(3)3(y-z)2-(2y+z)(-z+2y); (4)[x(x2y2-xy)-y(x2-x3y)]÷3x2y.
典例讲解
例3 分解因式:
(1)16a4-8a2b2+b4;(2)(x2+3x)2-(x-1)2.
解析 综合运用完全平方公式和平方差公式.注意分解要完全.
解:16a4-8a2b2+b4
=(4a2-b2)2
=(2a+b)2(2a-b)2
解:(x2+3x)2-(x-1)2
=(x2+3x+x-1)(x2+3x-x+1)
=(x2+4x-1)(x+1)2
强化练习
2 .分解因式:
(1)25x2-16y2; (2)(a-b)(x-y)-(b-a)(x+y);
教材124页第3题
强化练习
(3)a2-4ab+4b2; (4)4+12(x-y)+9(x-y)2.
强化练习
3. 已知 (x+y)2 = 25,(x-y)2 = 9,求 xy与 2 + y 的值.
教材125页第8题
强化练习
4. 求证: 当 n 是整数时,两个连续奇数的平方差(2n+1)2-(2n-1)2 是 8 的倍数.
教材125页第11题
典例讲解
例4 如图,水压机有四根空心钢立柱,每根高都是 18 m,外径 D 为 1 m 内径 d 为 0.4 m,每立方米钢的质量为7.8 t,求 4 根立柱的总质量 (π取3.14)
强化练习
5.某种产品的原料提价,因而厂家决定对产品进行提价,
现有三种方案:
(1)第一次提价 p%,第二次提价 q%;
(2)第一次提价 q%,第二次提价 p%;
(3)第一、二次提价均为
其中 p,q 是不相等的正数. 三种方案哪种提价最多?
(提示: 因为 p≠q,(p-q)2 = p2-2pq+q2>0,所以p2+q2 >2pq.)
教材125页第12题
强化练习
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
