活动单导学课程 苏教版高中数学选择性必修第一册第5章导数及其应用5.1.1 平均变化率(有答案)
文档属性
| 名称 | 活动单导学课程 苏教版高中数学选择性必修第一册第5章导数及其应用5.1.1 平均变化率(有答案) | 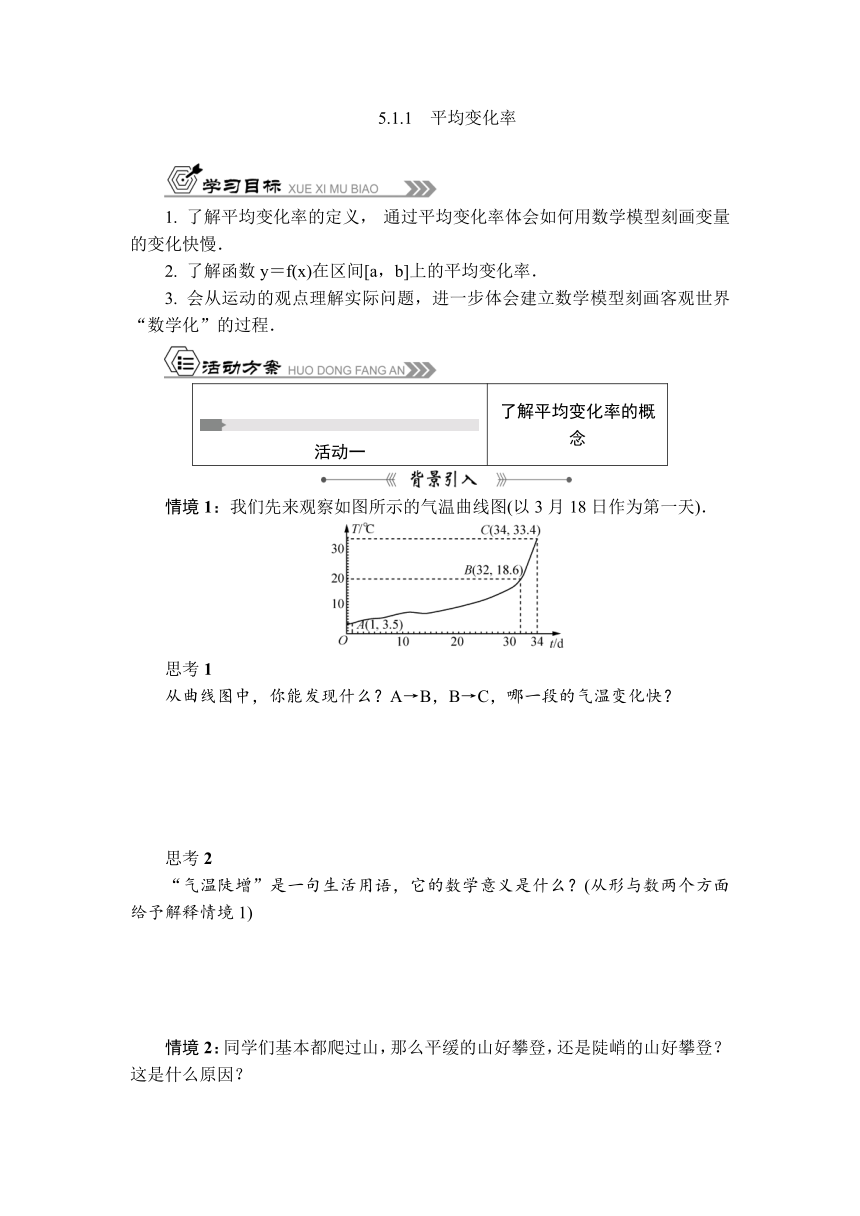 | |
| 格式 | docx | ||
| 文件大小 | 196.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-24 16:13:17 | ||
图片预览



文档简介
5.1.1 平均变化率
1. 了解平均变化率的定义, 通过平均变化率体会如何用数学模型刻画变量的变化快慢.
2. 了解函数y=f(x)在区间[a,b]上的平均变化率.
3. 会从运动的观点理解实际问题,进一步体会建立数学模型刻画客观世界“数学化”的过程.
活动一 了解平均变化率的概念
情境1:我们先来观察如图所示的气温曲线图(以3月18日作为第一天).
思考1
从曲线图中,你能发现什么?A→B,B→C,哪一段的气温变化快?
思考2
“气温陡增”是一句生活用语,它的数学意义是什么?(从形与数两个方面给予解释情境1)
情境2:同学们基本都爬过山,那么平缓的山好攀登,还是陡峭的山好攀登?这是什么原因?
情境3:在跑步的时候,在相同的时间内,跑得快累,还是跑得慢累?这是什么原因呢?
思考3
(1) 上述三个情境问题有什么共同点?
(2) 数学上用什么量来刻画变化的快慢?
1. 平均变化率.
思考4
结合上述问题总结平均变化率的概念.
思考5
试再举例说明平均变化率.
思考6
如果把上述三个情境问题都看成一个量为x,一个量为y,两者之间都有一个函数关系y=f(x),请用代数式子来表示平均变化率.
2. 函数的平均变化率.
思考7
试给出函数的平均变化率的概念.
解决函数平均变化率问题的关键是:
(1) 函数的解析式;
(2) 自变量的变化区间.
活动二 理解平均变化率的实际意义
例1 某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到第3个月以及第6个月到第12个月该婴儿体重的平均变化率.
例2 水经过虹吸管从容器甲流向容器乙,t s后容器甲中水的体积V(t)=5e-0.1t(单位:cm3),试计算第一个10 s内V的平均变化率.
活动三 了解函数y=f(x)在区间[a,b]上的平均变化率的求法
例3 已知函数f(x)=x2,分别计算函数f(x)在下列区间上的平均变化率:
(1) [1,3];
(2) [1,2];
(3) [1,1.1];
(4) [1,1.001].
例4 已知函数f(x)=-4x+1,g(x)=-2x分别计算在区间[-3,-1]和[0,5]上函数f(x)及g(x)平均变化率.
思考8
(1) 若将区间改为[1,1+Δx],结果如何?
(2) 一次函数在不同区间上的平均变化率有何特征?
活动四 了解平均变化率的几何意义
例5 已知曲线f(x)=x3上的两点P(1,1)和Q(1+Δx,1+Δy),求直线PQ的斜率,并求当Δx=0.1 时直线PQ的斜率.
1. 函数f(x)=x2+c(c∈R)区间上的平均变化率为( )
A. 2 B. 4 C. c D. 2c
2. 汽车行驶的路程s和时间t之间的函数图象如图,在时间段[t0,t1],[t1,t2],[t2,t3]上的平均速度分别为v1,v2,v3,则三者的大小关系为( )
A. v2=v3B. v1C. v1D. v23. (多选)甲工厂八年来某种产品的年产量y与时间x(单位:年)的函数关系如图所示,则下列说法中正确的是( )
A. 前四年该产品产量的增长速度越来越快
B. 前四年该产品产量的增长速度越来越慢
C. 第四年后该产品停止生产
D. 第四年后该产品的年产量保持不变
4. 函数y=2x2-4在区间[1,1+Δx]上的平均变化率为________.
5. 巍巍泰山为我国的五岳之首,有“天下第一山”之美誉.登泰山在当地有用“紧十八,慢十八,不紧不慢又十八”的俗语来形容爬十八盘的感受.下面是一段登山路线图,同样是登山,但是从A处到B处会感觉比较轻松,而从B处到C处会感觉比较吃力.试用数学语言给出解释.
参考答案与解析
【活动方案】
思考1:容易看出点B,C之间的曲线比点A,B之间的曲线更加“陡峭”.B→C段的气温变化快.
思考2:从形的角度:B→C段的曲线较A→B段更陡峭;从数的角度:气温在区间[1,32]上的平均变化率约为0.5;气温在区间[32,34]上的平均变化率为7.4.
情境2:平缓的山好攀登.因为山越陡峭,当爬山移动的水平距离变化量一定时,垂直距离的变化量越大,从而在陡峭的山攀登平均变化量就越大.
情境3:跑得快累.因为当时间变化量一定时,跑得快的位移变化量就大,从而在这时间内的平均变化量就大.
思考3:(1) 都和平均变化率有关.
(2) 平均变化率.
思考4:量化两点间陡峭程度,并称该比值为平均变化率.
思考5:略
思考6:y=f(x)=.
思考7:函数f(x)在区间[x1,x2]上的平均变化率为.
例1 从出生到第3个月,该婴儿体重的平均变化率为=1(kg/月),
从第6个月到第12个月,该婴儿体重的平均变化率为==0.4(kg/月).
例2 在区间[0,10]上,体积V的平均变化率为≈=-0.316 1(cm3/s),
即第一个10 s内容器甲中水的体积的平均变化率为-0.316 1 cm3/s(负号表示容器甲中的水在减少).
例3 (1) 函数f(x)在区间[1,3]上的平均变化率为=4.
(2) 函数f(x)在区间[1,2]上的平均变化率为=3.
(3) 函数f(x)在区间[1,1.1]上的平均变化率为=2.1.
(4) 函数f(x)在区间[1,1.001]上的平均变化率为=2.001.
例4 函数f(x)在区间[-3,-1]上的平均变化率为=-4,
函数f(x)在区间[0,5]上的平均变化率为=-4;
函数g(x)在区间[-3,-1]上的平均变化率为=-2;
函数g(x)在区间[0,5]上的平均变化率为=-2.
思考8:(1) 函数f(x)在区间[1,1+Δx]上的平均变化率为=-4,
函数g(x)在区间[1,1+Δx]上的平均变化率为=-2.
综上可知,结果保持不变.
(2) 一次函数在不同区间上的平均变化率等于斜率.
例5 因为Δy=f(1+Δx)-f(1)=(1+Δx)3-1=(Δx)3+3(Δx)2+3Δx,
所以直线PQ的斜率k==(Δx)2+3Δx+3.
设当Δx=0.1时,直线PQ的斜率为k1,则k1=0.12+3×0.1+3=3.31.
【检测反馈】
1. B 解析:===4.
2. C 解析:由题意,得v1=kOA,v2=kAB,v3=kBC,由题图易知kOA3. BD 解析:设y=f(x),由题图可知前四年该产品产量的增长速度越来越慢,故A错误,B正确;由题图可知从第四年开始产品产量不发生变化,且f(4)≠0,故C错误,D正确.故选BD.
4. 4+2Δx 解析:===4+2Δx.
5. 从A处到B处高度的平均变化率为==,从B处到C处高度的平均变化率为==.
由>,知山路从B处到C处比从A处到B处陡峭,
故从A处到B处会感觉比较轻松,从B处到C处会感觉比较吃力.
1. 了解平均变化率的定义, 通过平均变化率体会如何用数学模型刻画变量的变化快慢.
2. 了解函数y=f(x)在区间[a,b]上的平均变化率.
3. 会从运动的观点理解实际问题,进一步体会建立数学模型刻画客观世界“数学化”的过程.
活动一 了解平均变化率的概念
情境1:我们先来观察如图所示的气温曲线图(以3月18日作为第一天).
思考1
从曲线图中,你能发现什么?A→B,B→C,哪一段的气温变化快?
思考2
“气温陡增”是一句生活用语,它的数学意义是什么?(从形与数两个方面给予解释情境1)
情境2:同学们基本都爬过山,那么平缓的山好攀登,还是陡峭的山好攀登?这是什么原因?
情境3:在跑步的时候,在相同的时间内,跑得快累,还是跑得慢累?这是什么原因呢?
思考3
(1) 上述三个情境问题有什么共同点?
(2) 数学上用什么量来刻画变化的快慢?
1. 平均变化率.
思考4
结合上述问题总结平均变化率的概念.
思考5
试再举例说明平均变化率.
思考6
如果把上述三个情境问题都看成一个量为x,一个量为y,两者之间都有一个函数关系y=f(x),请用代数式子来表示平均变化率.
2. 函数的平均变化率.
思考7
试给出函数的平均变化率的概念.
解决函数平均变化率问题的关键是:
(1) 函数的解析式;
(2) 自变量的变化区间.
活动二 理解平均变化率的实际意义
例1 某婴儿从出生到第12个月的体重变化如图所示,试分别计算从出生到第3个月以及第6个月到第12个月该婴儿体重的平均变化率.
例2 水经过虹吸管从容器甲流向容器乙,t s后容器甲中水的体积V(t)=5e-0.1t(单位:cm3),试计算第一个10 s内V的平均变化率.
活动三 了解函数y=f(x)在区间[a,b]上的平均变化率的求法
例3 已知函数f(x)=x2,分别计算函数f(x)在下列区间上的平均变化率:
(1) [1,3];
(2) [1,2];
(3) [1,1.1];
(4) [1,1.001].
例4 已知函数f(x)=-4x+1,g(x)=-2x分别计算在区间[-3,-1]和[0,5]上函数f(x)及g(x)平均变化率.
思考8
(1) 若将区间改为[1,1+Δx],结果如何?
(2) 一次函数在不同区间上的平均变化率有何特征?
活动四 了解平均变化率的几何意义
例5 已知曲线f(x)=x3上的两点P(1,1)和Q(1+Δx,1+Δy),求直线PQ的斜率,并求当Δx=0.1 时直线PQ的斜率.
1. 函数f(x)=x2+c(c∈R)区间上的平均变化率为( )
A. 2 B. 4 C. c D. 2c
2. 汽车行驶的路程s和时间t之间的函数图象如图,在时间段[t0,t1],[t1,t2],[t2,t3]上的平均速度分别为v1,v2,v3,则三者的大小关系为( )
A. v2=v3
A. 前四年该产品产量的增长速度越来越快
B. 前四年该产品产量的增长速度越来越慢
C. 第四年后该产品停止生产
D. 第四年后该产品的年产量保持不变
4. 函数y=2x2-4在区间[1,1+Δx]上的平均变化率为________.
5. 巍巍泰山为我国的五岳之首,有“天下第一山”之美誉.登泰山在当地有用“紧十八,慢十八,不紧不慢又十八”的俗语来形容爬十八盘的感受.下面是一段登山路线图,同样是登山,但是从A处到B处会感觉比较轻松,而从B处到C处会感觉比较吃力.试用数学语言给出解释.
参考答案与解析
【活动方案】
思考1:容易看出点B,C之间的曲线比点A,B之间的曲线更加“陡峭”.B→C段的气温变化快.
思考2:从形的角度:B→C段的曲线较A→B段更陡峭;从数的角度:气温在区间[1,32]上的平均变化率约为0.5;气温在区间[32,34]上的平均变化率为7.4.
情境2:平缓的山好攀登.因为山越陡峭,当爬山移动的水平距离变化量一定时,垂直距离的变化量越大,从而在陡峭的山攀登平均变化量就越大.
情境3:跑得快累.因为当时间变化量一定时,跑得快的位移变化量就大,从而在这时间内的平均变化量就大.
思考3:(1) 都和平均变化率有关.
(2) 平均变化率.
思考4:量化两点间陡峭程度,并称该比值为平均变化率.
思考5:略
思考6:y=f(x)=.
思考7:函数f(x)在区间[x1,x2]上的平均变化率为.
例1 从出生到第3个月,该婴儿体重的平均变化率为=1(kg/月),
从第6个月到第12个月,该婴儿体重的平均变化率为==0.4(kg/月).
例2 在区间[0,10]上,体积V的平均变化率为≈=-0.316 1(cm3/s),
即第一个10 s内容器甲中水的体积的平均变化率为-0.316 1 cm3/s(负号表示容器甲中的水在减少).
例3 (1) 函数f(x)在区间[1,3]上的平均变化率为=4.
(2) 函数f(x)在区间[1,2]上的平均变化率为=3.
(3) 函数f(x)在区间[1,1.1]上的平均变化率为=2.1.
(4) 函数f(x)在区间[1,1.001]上的平均变化率为=2.001.
例4 函数f(x)在区间[-3,-1]上的平均变化率为=-4,
函数f(x)在区间[0,5]上的平均变化率为=-4;
函数g(x)在区间[-3,-1]上的平均变化率为=-2;
函数g(x)在区间[0,5]上的平均变化率为=-2.
思考8:(1) 函数f(x)在区间[1,1+Δx]上的平均变化率为=-4,
函数g(x)在区间[1,1+Δx]上的平均变化率为=-2.
综上可知,结果保持不变.
(2) 一次函数在不同区间上的平均变化率等于斜率.
例5 因为Δy=f(1+Δx)-f(1)=(1+Δx)3-1=(Δx)3+3(Δx)2+3Δx,
所以直线PQ的斜率k==(Δx)2+3Δx+3.
设当Δx=0.1时,直线PQ的斜率为k1,则k1=0.12+3×0.1+3=3.31.
【检测反馈】
1. B 解析:===4.
2. C 解析:由题意,得v1=kOA,v2=kAB,v3=kBC,由题图易知kOA
4. 4+2Δx 解析:===4+2Δx.
5. 从A处到B处高度的平均变化率为==,从B处到C处高度的平均变化率为==.
由>,知山路从B处到C处比从A处到B处陡峭,
故从A处到B处会感觉比较轻松,从B处到C处会感觉比较吃力.
