整式的乘法[上学期]
图片预览










文档简介
课件42张PPT。15.2.4整式的乘法钟凌峰共两课时复习提问?2、幂的乘方:3、积的乘方:1、同底数幂的乘法法则:其中 m , n都是正整数小测试题 计算:
(1) (103)5 (2) (-x2)7
(3) (-3xy2)3 (4) (ab)10
(5) m3(-m)6 (-m)5
(6) (x+y)2· (x+y)3
(7)
(8) (-2a3)2-(-4a2)3-[-(3a)2]3 1015-x14-27x3y6a10b10=-m3m6m5=-m14(x+y)5 (1)什么是单项式? (2)什么叫单项式的系数? (3)什么叫单项式的次数? 回忆1由数字与字母(或字母与字母)的 乘积组成的,
这样的代数式叫做单项式.单项式中的数字因数 叫做这个单项式的系数。一个单项式中,所有 字母的指数的和 叫做这个单项式的次数。回忆2你知道这是什么吗?ab=ba你能说出结果吗?x2 x1=x3 这是前面才学过的同底数幂的乘法及积的乘方.问题 光的速度约为3×105千米/秒,太阳光照射到地球上需要的时间大约是5 ×102秒,你知道地球与太阳的距离约是多少千米吗?地球与太阳的距离约是
(3×105) ×(5×102)千米. =(3 × 5) ×(105 × 102)
= 15 ×107
=1.5 ×108(千米)讨论
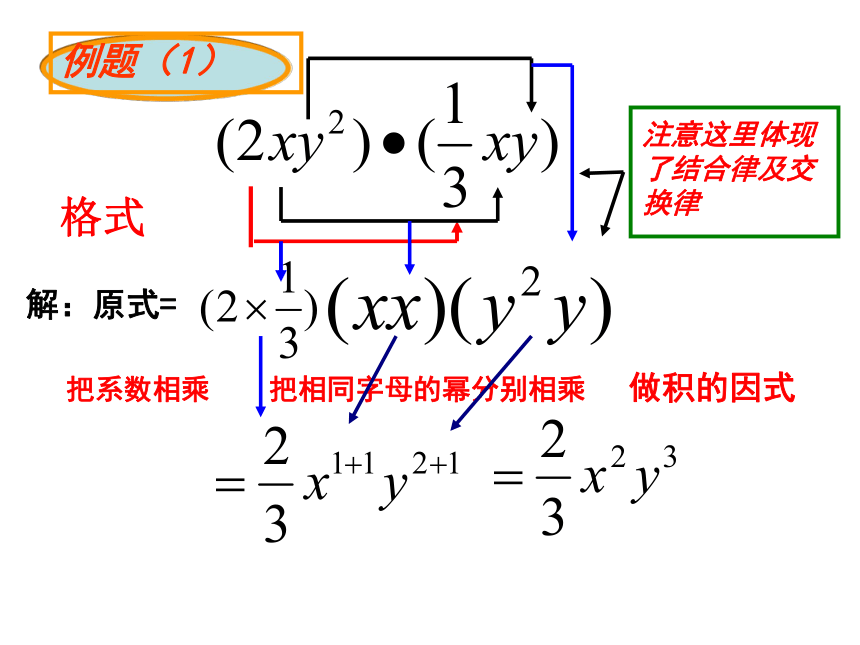
比如ac5?bc2怎样计算这个式子?ac5?bc2是两个单项式ac5与bc2相乘,我们可以利用乘法交换律,结合律及同底数幂的运算性质来计算:ac5?bc2=(a ?b)?(c5?c2) = abc5+2=abc7.试一试计算:(1) 2c5.5c2; (2) (-5a2b3).(-4b2c)谁能告诉大家怎样进行单项式乘法? 单项式与单项式相乘,把它们的系数、相同字母分别相乘 ,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。(1)系数相乘(2)相同字母的幂相乘(3)其余字母连同它的指数不变, 作为积的因式。例题(1)格式解:原式=把系数相乘把相同字母的幂分别相乘做积的因式把系数相乘作为积的因式解:原式=例题 (2)例题 (3)解:原式科学记数法表示的数也是单项式可以了吗?科学记数法是有规定的。结论一定要化简下面的计算对不 对?如果不对,怎样改正?正确请你当医生赛一赛:计算以下各题:(1)6x2·3xy (2)(2ab2)·( -3ab ) (3)(mn)2 ·(-m2n) (4) (-5amb) · (-2b2) (5)(4×106)(8×102) 算一算:例2、(-5a2b)· (-3a) · (-2ab2c)(1) (-3ab)· (-a2c)· 6ab2=18a4b3c试一试:(2) (2ab2)2 · (-3a2) + a3b· 2ab3=-10a4b4(1)大长方形的长 ,宽为 ,
面积 . (2)①、②、③三个小长方形的面积分别是
.面积和 。(3)由(1)、(2)得出等式
.①②③(a+b+c)ma、mb、mcm(a+b+c)看图说明 = ma+mb+mcmm(a+b+c) ma+mb+mc单项式与多项式相乘法则: 单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加。m(a+b+c)=ma+mb+mc计算:
(1)(- 2a) ? (2a 2 - 3a + 1)解原式= (- 2a) ? 2a 2 +(- 2a) ?( - 3a)+(- 2a) ? 1= - 4a3+6a2 - 2a(分配律)(单项式乘法法则)例2
(2) (- 4x) (2x2+3x-1)解:原式=(- 4x) ?2x2+(- 4x)?3x+(- 4x)?(-1) = - 8x3- 12x2+4x单项式与多项式相乘时,分两个阶段:①按分配律把乘积写成单项式与单项式乘积的代数和的形式;②单项式的乘法运算。解:原式= a2b3– a2b2注意: 1. 单项式与多项式相乘,结果是一个多项式,其项数与因式中多项式的项数相同.2. 计算时,要注意符号问题,多项式中每一项都包括它前面的符号,特别要注意系数的符号. 3.不要出现漏乘现象,运算要有顺序。问题:1、单项式与多项式的乘法法则是什么?并说出下列各题的结果。
(1)6a4· (-2a2)= (2)(-ya) ·4y=
(3) (4)
-12a6-4ya+1问题如图,为了扩大街心花园的绿地面积,把一块原长a米、宽m米的长方形绿地,增长了b米,加宽了n米。你能用几种方法求出扩大后的绿地的面积?扩大后的绿地可以看成长为(a+b)米,宽为(m+n)米的长方形,所以这块绿地的面积为(a+b)(m+n)米2(am+an+bm+bn)米2ambmanbn因此 (a+b) (m+n)=am+an+bm+bn(a+b) (m+n)计算:(a+b) (m+n),可以先把其中的一个多项式,如(m+n),看成一个整体,运用单项式与多项式相乘的法则,得=a(m+n)+b(m+n)再利用单项式与多项式相乘的法则,得a(m+n)+b(m+n)=am+an+bm+bn 总体一看,(a+b) (m+n)的结果可以看作由a+b的每一项乘m+n的每一项,再把所得的积相加而得到的,即(a+b) (m+n)=am+an+bm+bn 多项式与多项式相乘,先用一个多项式的每一项乘另一多项式的每一项,再把所得的积相加。例4、计算:
(1)(3x + 1)(x - 2) (2) (x – 8y)(x – y)解: (1) (3x + 1)(x - 2)=(3x) ·x + (3x) ·(-2) +1·x + 1×(-2)=3x2 – 6x + x - 2=3x2 – 5x - 2(2) (x – 8y)(x – y)= x2 – xy – 8xy + 8y2= x2 – 9xy + 8y2例5、计算:
(1)
(2)巩固练习 1、口算: (1) (m + n)(u + v) (2) (x + y)(a - b)
(3) (p - q)(x + y) (4) (a - b)(c - d)
2、计算: (1) (2n + 6)(n - 3) (2) (2x + 3)(3x - 1)
(3) (2a – 3b)(a + 5b) (4) (3x – 2x)(3x - 2y)
(5) (6) (2x + 5)(2x + 5)1.4(a-b+1)=___________________4a-4b+42.3x(2x-y2)=___________________6x2-3xy23.-3x(2x-5y+6z)=___________________-6x2+15xy-18xz4.(-2a2)(-a-2b+c)=___________________2a3+4a2b-2a2c小试身手: 火眼金睛:(1)( - 3x)(2x - 3y)=6x2 - 9xy ( )
(2) 5x(2x2 - 3x+1)=10x3 - 15x2 ( )
(3) am(am-a2+1)=a2m-a2m+am=am ( )
(4) (-2x)?(ax+b-3)=-2ax2-2bx-6x( )
××××注意:各项符号的确定!防止漏项哦!求值:
yn(yn + 9y - 12) – 3(3yn+1 - 4yn),
其中y= - 3,n=2.解: yn(yn + 9y - 12) – 3(3yn+1 - 4yn)= y 2n+ 9yn+1- 12 yn– 9yn+1 +12 yn= y 2n当y= - 3,n=2时,原式=(- 3)4=81虞老师今年1月看中了杜桥蓝盾的一套房屋,为了想了解客厅的面积,用自己的步长(步长为a米)去测量客厅,量得客厅长15步,宽14步,请问客厅有多少平方米?请你帮忙:15a·14a=210a2 (m2)虞老师对刚才的那套房屋比较满意,决定购买后打算把除卧室以外的其它部分全都铺上地砖,问至少需要多少平方米的地转?
如果某种地转的价格是a元/平方米,那么购买地砖至少需要多少元?请你帮忙:4x· 2y+2x· y+x· y=8xy+2xy+xy=11xy11xy· a=11axy探索与思考解:ab(a2b5-ab3-b)=a3b6-a2b4-ab2=(ab2)3-(ab2)2-ab2当ab2=-6时,原式=( - 6)3 -( - 6)2- (- 6)=-246挑战自我:2、(-xya) · nx2y2= 6x3y4 则 n = __, a = __-623、若(am+1bn+2)(a2n-1b2m)=a5b3 则m+n的值为 ( )(A) 1 (B)2 (C)3 (D) -3 BB挑战自我: 动脑筋: 计算下列图形的面积?方法1:=方法2:=方法3:方法4:ab-(a-t) (b-t)=at+bt-t23、计算:
(x + 1)( x2 – 2x + 3)
(x – 1)(x2 + x + 1)
(4x – 3)(5x2 – 4x + 7)
(3x + 2)(3x – 2)(x2 – 1)
(5) (3a – 2)(a – 1) + (a + 1)(a + 2)
(6) (2x2 – 1)(x – 4) - ( x2 + 3)(2x – 5)作业: 1、计算:
(1) (3x + 1)(x + 2) (2) (4y - 1)(y - 5)
(2x - 3)(4x - 1) (4) (3a +2)(4a + 1)
(5 ) (7x2 - 8y2)(x2 + 3y2) (6)(9m - 4n)(9m - 4n)
(7) (8) (x + 2)(x - 2)(x2 + 4)
(9) (1 - 2x + 4x2)(1 + 2x)
(x - y)(x2 + xy + y2)
(11) 5x(x2+2x +1) - (2x + 3)(x - 5)
(12) (3x – y)(y + 3x) - (4x - 3y)(3y + 4x)2、计算:
(1) (x + 3)(x + 2)
(2) (a + 5)(a - 3)
(3) (x - 5)(x + 3)
(4) (m + 2)(m - 8)
(5)先化简,再求值
(3x + 1)(2x - 3) - (6x - 5)(x - 4)
其中x = -2课时小结: 1、单项式与多项式相乘的实质是把单项式乘以多项式转化为单项式乘法 2、相关的混合运算,要弄清顺序
(1)单项式乘以单项式或单项式乘以多项式。
(2)整式加减注意最后应合并同类项。几点注意: 1、 单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定:同号相乘得正,异号相乘得负 2.不要出现漏乘现象3、运算要有顺序:先乘方,再乘除,最后加减。有括号一般先去括号(小→大)转化思想单项式与单项式相乘的法则生活中处处有数学思想方法收获应用收获知识收获谈收获老师们、同学们、再见!
(1) (103)5 (2) (-x2)7
(3) (-3xy2)3 (4) (ab)10
(5) m3(-m)6 (-m)5
(6) (x+y)2· (x+y)3
(7)
(8) (-2a3)2-(-4a2)3-[-(3a)2]3 1015-x14-27x3y6a10b10=-m3m6m5=-m14(x+y)5 (1)什么是单项式? (2)什么叫单项式的系数? (3)什么叫单项式的次数? 回忆1由数字与字母(或字母与字母)的 乘积组成的,
这样的代数式叫做单项式.单项式中的数字因数 叫做这个单项式的系数。一个单项式中,所有 字母的指数的和 叫做这个单项式的次数。回忆2你知道这是什么吗?ab=ba你能说出结果吗?x2 x1=x3 这是前面才学过的同底数幂的乘法及积的乘方.问题 光的速度约为3×105千米/秒,太阳光照射到地球上需要的时间大约是5 ×102秒,你知道地球与太阳的距离约是多少千米吗?地球与太阳的距离约是
(3×105) ×(5×102)千米. =(3 × 5) ×(105 × 102)
= 15 ×107
=1.5 ×108(千米)讨论
比如ac5?bc2怎样计算这个式子?ac5?bc2是两个单项式ac5与bc2相乘,我们可以利用乘法交换律,结合律及同底数幂的运算性质来计算:ac5?bc2=(a ?b)?(c5?c2) = abc5+2=abc7.试一试计算:(1) 2c5.5c2; (2) (-5a2b3).(-4b2c)谁能告诉大家怎样进行单项式乘法? 单项式与单项式相乘,把它们的系数、相同字母分别相乘 ,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。(1)系数相乘(2)相同字母的幂相乘(3)其余字母连同它的指数不变, 作为积的因式。例题(1)格式解:原式=把系数相乘把相同字母的幂分别相乘做积的因式把系数相乘作为积的因式解:原式=例题 (2)例题 (3)解:原式科学记数法表示的数也是单项式可以了吗?科学记数法是有规定的。结论一定要化简下面的计算对不 对?如果不对,怎样改正?正确请你当医生赛一赛:计算以下各题:(1)6x2·3xy (2)(2ab2)·( -3ab ) (3)(mn)2 ·(-m2n) (4) (-5amb) · (-2b2) (5)(4×106)(8×102) 算一算:例2、(-5a2b)· (-3a) · (-2ab2c)(1) (-3ab)· (-a2c)· 6ab2=18a4b3c试一试:(2) (2ab2)2 · (-3a2) + a3b· 2ab3=-10a4b4(1)大长方形的长 ,宽为 ,
面积 . (2)①、②、③三个小长方形的面积分别是
.面积和 。(3)由(1)、(2)得出等式
.①②③(a+b+c)ma、mb、mcm(a+b+c)看图说明 = ma+mb+mcmm(a+b+c) ma+mb+mc单项式与多项式相乘法则: 单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加。m(a+b+c)=ma+mb+mc计算:
(1)(- 2a) ? (2a 2 - 3a + 1)解原式= (- 2a) ? 2a 2 +(- 2a) ?( - 3a)+(- 2a) ? 1= - 4a3+6a2 - 2a(分配律)(单项式乘法法则)例2
(2) (- 4x) (2x2+3x-1)解:原式=(- 4x) ?2x2+(- 4x)?3x+(- 4x)?(-1) = - 8x3- 12x2+4x单项式与多项式相乘时,分两个阶段:①按分配律把乘积写成单项式与单项式乘积的代数和的形式;②单项式的乘法运算。解:原式= a2b3– a2b2注意: 1. 单项式与多项式相乘,结果是一个多项式,其项数与因式中多项式的项数相同.2. 计算时,要注意符号问题,多项式中每一项都包括它前面的符号,特别要注意系数的符号. 3.不要出现漏乘现象,运算要有顺序。问题:1、单项式与多项式的乘法法则是什么?并说出下列各题的结果。
(1)6a4· (-2a2)= (2)(-ya) ·4y=
(3) (4)
-12a6-4ya+1问题如图,为了扩大街心花园的绿地面积,把一块原长a米、宽m米的长方形绿地,增长了b米,加宽了n米。你能用几种方法求出扩大后的绿地的面积?扩大后的绿地可以看成长为(a+b)米,宽为(m+n)米的长方形,所以这块绿地的面积为(a+b)(m+n)米2(am+an+bm+bn)米2ambmanbn因此 (a+b) (m+n)=am+an+bm+bn(a+b) (m+n)计算:(a+b) (m+n),可以先把其中的一个多项式,如(m+n),看成一个整体,运用单项式与多项式相乘的法则,得=a(m+n)+b(m+n)再利用单项式与多项式相乘的法则,得a(m+n)+b(m+n)=am+an+bm+bn 总体一看,(a+b) (m+n)的结果可以看作由a+b的每一项乘m+n的每一项,再把所得的积相加而得到的,即(a+b) (m+n)=am+an+bm+bn 多项式与多项式相乘,先用一个多项式的每一项乘另一多项式的每一项,再把所得的积相加。例4、计算:
(1)(3x + 1)(x - 2) (2) (x – 8y)(x – y)解: (1) (3x + 1)(x - 2)=(3x) ·x + (3x) ·(-2) +1·x + 1×(-2)=3x2 – 6x + x - 2=3x2 – 5x - 2(2) (x – 8y)(x – y)= x2 – xy – 8xy + 8y2= x2 – 9xy + 8y2例5、计算:
(1)
(2)巩固练习 1、口算: (1) (m + n)(u + v) (2) (x + y)(a - b)
(3) (p - q)(x + y) (4) (a - b)(c - d)
2、计算: (1) (2n + 6)(n - 3) (2) (2x + 3)(3x - 1)
(3) (2a – 3b)(a + 5b) (4) (3x – 2x)(3x - 2y)
(5) (6) (2x + 5)(2x + 5)1.4(a-b+1)=___________________4a-4b+42.3x(2x-y2)=___________________6x2-3xy23.-3x(2x-5y+6z)=___________________-6x2+15xy-18xz4.(-2a2)(-a-2b+c)=___________________2a3+4a2b-2a2c小试身手: 火眼金睛:(1)( - 3x)(2x - 3y)=6x2 - 9xy ( )
(2) 5x(2x2 - 3x+1)=10x3 - 15x2 ( )
(3) am(am-a2+1)=a2m-a2m+am=am ( )
(4) (-2x)?(ax+b-3)=-2ax2-2bx-6x( )
××××注意:各项符号的确定!防止漏项哦!求值:
yn(yn + 9y - 12) – 3(3yn+1 - 4yn),
其中y= - 3,n=2.解: yn(yn + 9y - 12) – 3(3yn+1 - 4yn)= y 2n+ 9yn+1- 12 yn– 9yn+1 +12 yn= y 2n当y= - 3,n=2时,原式=(- 3)4=81虞老师今年1月看中了杜桥蓝盾的一套房屋,为了想了解客厅的面积,用自己的步长(步长为a米)去测量客厅,量得客厅长15步,宽14步,请问客厅有多少平方米?请你帮忙:15a·14a=210a2 (m2)虞老师对刚才的那套房屋比较满意,决定购买后打算把除卧室以外的其它部分全都铺上地砖,问至少需要多少平方米的地转?
如果某种地转的价格是a元/平方米,那么购买地砖至少需要多少元?请你帮忙:4x· 2y+2x· y+x· y=8xy+2xy+xy=11xy11xy· a=11axy探索与思考解:ab(a2b5-ab3-b)=a3b6-a2b4-ab2=(ab2)3-(ab2)2-ab2当ab2=-6时,原式=( - 6)3 -( - 6)2- (- 6)=-246挑战自我:2、(-xya) · nx2y2= 6x3y4 则 n = __, a = __-623、若(am+1bn+2)(a2n-1b2m)=a5b3 则m+n的值为 ( )(A) 1 (B)2 (C)3 (D) -3 BB挑战自我: 动脑筋: 计算下列图形的面积?方法1:=方法2:=方法3:方法4:ab-(a-t) (b-t)=at+bt-t23、计算:
(x + 1)( x2 – 2x + 3)
(x – 1)(x2 + x + 1)
(4x – 3)(5x2 – 4x + 7)
(3x + 2)(3x – 2)(x2 – 1)
(5) (3a – 2)(a – 1) + (a + 1)(a + 2)
(6) (2x2 – 1)(x – 4) - ( x2 + 3)(2x – 5)作业: 1、计算:
(1) (3x + 1)(x + 2) (2) (4y - 1)(y - 5)
(2x - 3)(4x - 1) (4) (3a +2)(4a + 1)
(5 ) (7x2 - 8y2)(x2 + 3y2) (6)(9m - 4n)(9m - 4n)
(7) (8) (x + 2)(x - 2)(x2 + 4)
(9) (1 - 2x + 4x2)(1 + 2x)
(x - y)(x2 + xy + y2)
(11) 5x(x2+2x +1) - (2x + 3)(x - 5)
(12) (3x – y)(y + 3x) - (4x - 3y)(3y + 4x)2、计算:
(1) (x + 3)(x + 2)
(2) (a + 5)(a - 3)
(3) (x - 5)(x + 3)
(4) (m + 2)(m - 8)
(5)先化简,再求值
(3x + 1)(2x - 3) - (6x - 5)(x - 4)
其中x = -2课时小结: 1、单项式与多项式相乘的实质是把单项式乘以多项式转化为单项式乘法 2、相关的混合运算,要弄清顺序
(1)单项式乘以单项式或单项式乘以多项式。
(2)整式加减注意最后应合并同类项。几点注意: 1、 单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定:同号相乘得正,异号相乘得负 2.不要出现漏乘现象3、运算要有顺序:先乘方,再乘除,最后加减。有括号一般先去括号(小→大)转化思想单项式与单项式相乘的法则生活中处处有数学思想方法收获应用收获知识收获谈收获老师们、同学们、再见!
