整式的乘法3[上学期]
图片预览







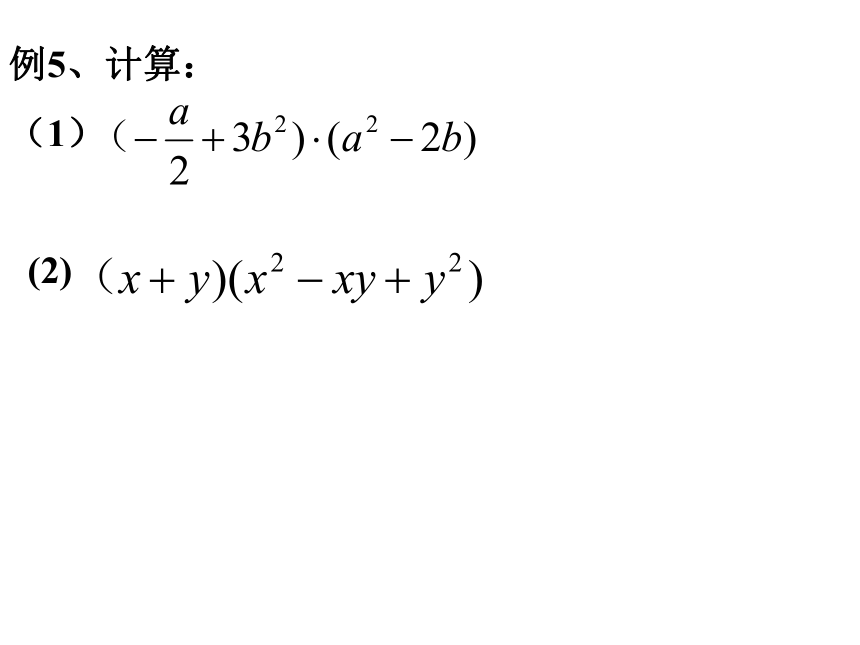
文档简介
课件23张PPT。整式的乘法(3)复习提问?2、幂的乘方:3、积的乘方:1、同底数幂的乘法法则:其中 m , n都是正整数单项式与多项式相乘法则: 单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加。m(a+b+c)=ma+mb+mc1.4(a-b+1)=___________________4a-4b+42.3x(2x-y2)=___________________6x2-3xy23.-3x(2x-5y+6z)=___________________-6x2+15xy-18xz4.(-2a2)(-a-2b+c)=___________________2a3+4a2b-2a2c小试身手: 火眼金睛:(1)( - 3x)(2x - 3y)=6x2 - 9xy ( )
(2) 5x(2x2 - 3x+1)=10x3 - 15x2 ( )
(3) am(am-a2+1)=a2m-a2m+am=am ( )
(4) (-2x)?(ax+b-3)=-2ax2-2bx-6x( )
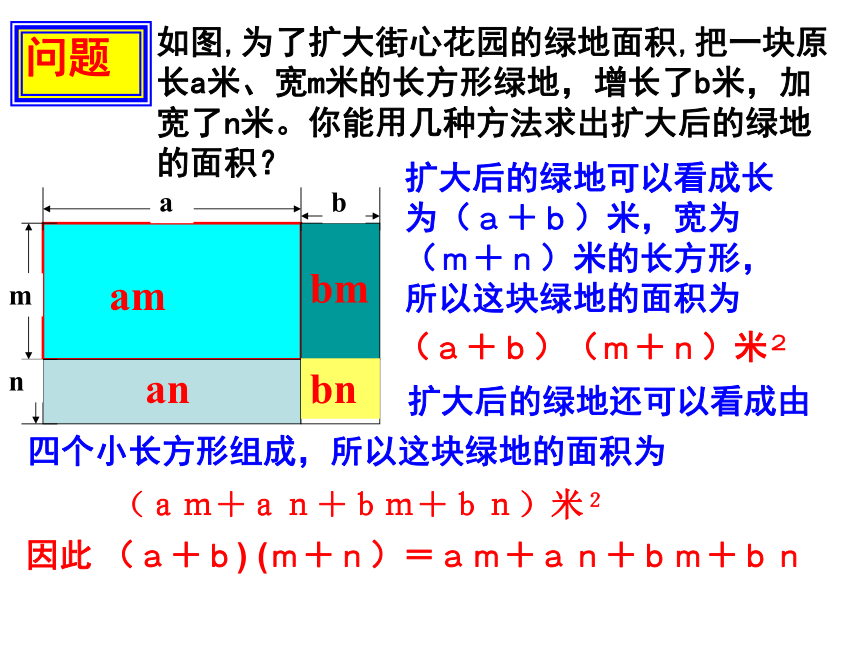
××××注意:各项符号的确定!防止漏项哦!问题如图,为了扩大街心花园的绿地面积,把一块原长a米、宽m米的长方形绿地,增长了b米,加宽了n米。你能用几种方法求出扩大后的绿地的面积?扩大后的绿地可以看成长为(a+b)米,宽为(m+n)米的长方形,所以这块绿地的面积为(a+b)(m+n)米2(am+an+bm+bn)米2ambmanbn因此 (a+b) (m+n)=am+an+bm+bn(a+b) (m+n)计算:(a+b) (m+n),可以先把其中的一个多项式,如(m+n),看成一个整体,运用单项式与多项式相乘的法则,得=a(m+n)+b(m+n)再利用单项式与多项式相乘的法则,得a(m+n)+b(m+n)=am+an+bm+bn 总体一看,(a+b) (m+n)的结果可以看作由a+b的每一项乘m+n的每一项,再把所得的积相加而得到的,即(a+b) (m+n)=am+an+bm+bn 多项式与多项式相乘,先用一个多项式的每一项乘另一多项式的每一项,再把所得的积相加。例4、计算:
(1)(3x + 1)(x - 2) (2) (x – 8y)(x – y)解: (1) (3x + 1)(x - 2)=(3x) ·x + (3x) ·(-2) +1·x + 1×(-2)=3x2 – 6x + x - 2=3x2 – 5x - 2(2) (x – 8y)(x – y)= x2 – xy – 8xy + 8y2= x2 – 9xy + 8y2例5、计算:
(1)
(2)巩固练习 1、口算: (1) (m + n)(u + v) (2) (x + y)(a - b)
(3) (p - q)(x + y) (4) (a - b)(c - d)
2、计算: (1) (2n + 6)(n - 3) (2) (2x + 3)(3x - 1)
(3) (2a – 3b)(a + 5b) (4) (3x – 2x)(3x - 2y)
(5) (6) (2x + 5)(2x + 5)求值:
yn(yn + 9y - 12) – 3(3yn+1 - 4yn),
其中y= - 3,n=2.解: yn(yn + 9y - 12) – 3(3yn+1 - 4yn)= y 2n+ 9yn+1- 12 yn– 9yn+1 +12 yn= y 2n当y= - 3,n=2时,原式=(- 3)4=81虞老师今年1月看中了杜桥蓝盾的一套房屋,为了想了解客厅的面积,用自己的步长(步长为a米)去测量客厅,量得客厅长15步,宽14步,请问客厅有多少平方米?请你帮忙:15a·14a=210a2 (m2)虞老师对刚才的那套房屋比较满意,决定购买后打算把除卧室以外的其它部分全都铺上地砖,问至少需要多少平方米的地转?
如果某种地转的价格是a元/平方米,那么购买地砖至少需要多少元?请你帮忙:4x· 2y+2x· y+x· y=8xy+2xy+xy=11xy11xy· a=11axy探索与思考解:ab(a2b5-ab3-b)=a3b6-a2b4-ab2=(ab2)3-(ab2)2-ab2当ab2=-6时,原式=( - 6)3 -( - 6)2- (- 6)=-2463、若(am+1bn+2)(a2n-1b2m)=a5b3 则m+n的值为 ( )(A) 1 (B)2 (C)3 (D) -3 BB挑战自我: 动脑筋: 计算下列图形的面积?方法1:=方法2:=方法3:方法4:ab-(a-t) (b-t)=at+bt-t23、计算:
(x + 1)( x2 – 2x + 3)
(x – 1)(x2 + x + 1)
(4x – 3)(5x2 – 4x + 7)
(3x + 2)(3x – 2)(x2 – 1)
(5) (3a – 2)(a – 1) + (a + 1)(a + 2)
(6) (2x2 – 1)(x – 4) - ( x2 + 3)(2x – 5)作业: 1、计算:
(1) (3x + 1)(x + 2) (2) (4y - 1)(y - 5)
(2x - 3)(4x - 1) (4) (3a +2)(4a + 1)
(5 ) (7x2 - 8y2)(x2 + 3y2) (6)(9m - 4n)(9m - 4n)
(7) (8) (x + 2)(x - 2)(x2 + 4)
(9) (1 - 2x + 4x2)(1 + 2x)
(x - y)(x2 + xy + y2)
(11) 5x(x2+2x +1) - (2x + 3)(x - 5)
(12) (3x – y)(y + 3x) - (4x - 3y)(3y + 4x)2、计算:
(1) (x + 3)(x + 2)
(2) (a + 5)(a - 3)
(3) (x - 5)(x + 3)
(4) (m + 2)(m - 8)
(5)先化简,再求值
(3x + 1)(2x - 3) - (6x - 5)(x - 4)
其中x = -2课时小结: 1、单项式与多项式相乘的实质是把单项式乘以多项式转化为单项式乘法 2、相关的混合运算,要弄清顺序
(1)单项式乘以单项式或单项式乘以多项式。
(2)整式加减注意最后应合并同类项。几点注意: 1、 单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定:同号相乘得正,异号相乘得负 2.不要出现漏乘现象3、运算要有顺序:先乘方,再乘除,最后加减。有括号一般先去括号(小→大)转化思想单项式与单项式相乘的法则生活中处处有数学思想方法收获应用收获知识收获谈收获老师们、同学们、再见!
(2) 5x(2x2 - 3x+1)=10x3 - 15x2 ( )
(3) am(am-a2+1)=a2m-a2m+am=am ( )
(4) (-2x)?(ax+b-3)=-2ax2-2bx-6x( )
××××注意:各项符号的确定!防止漏项哦!问题如图,为了扩大街心花园的绿地面积,把一块原长a米、宽m米的长方形绿地,增长了b米,加宽了n米。你能用几种方法求出扩大后的绿地的面积?扩大后的绿地可以看成长为(a+b)米,宽为(m+n)米的长方形,所以这块绿地的面积为(a+b)(m+n)米2(am+an+bm+bn)米2ambmanbn因此 (a+b) (m+n)=am+an+bm+bn(a+b) (m+n)计算:(a+b) (m+n),可以先把其中的一个多项式,如(m+n),看成一个整体,运用单项式与多项式相乘的法则,得=a(m+n)+b(m+n)再利用单项式与多项式相乘的法则,得a(m+n)+b(m+n)=am+an+bm+bn 总体一看,(a+b) (m+n)的结果可以看作由a+b的每一项乘m+n的每一项,再把所得的积相加而得到的,即(a+b) (m+n)=am+an+bm+bn 多项式与多项式相乘,先用一个多项式的每一项乘另一多项式的每一项,再把所得的积相加。例4、计算:
(1)(3x + 1)(x - 2) (2) (x – 8y)(x – y)解: (1) (3x + 1)(x - 2)=(3x) ·x + (3x) ·(-2) +1·x + 1×(-2)=3x2 – 6x + x - 2=3x2 – 5x - 2(2) (x – 8y)(x – y)= x2 – xy – 8xy + 8y2= x2 – 9xy + 8y2例5、计算:
(1)
(2)巩固练习 1、口算: (1) (m + n)(u + v) (2) (x + y)(a - b)
(3) (p - q)(x + y) (4) (a - b)(c - d)
2、计算: (1) (2n + 6)(n - 3) (2) (2x + 3)(3x - 1)
(3) (2a – 3b)(a + 5b) (4) (3x – 2x)(3x - 2y)
(5) (6) (2x + 5)(2x + 5)求值:
yn(yn + 9y - 12) – 3(3yn+1 - 4yn),
其中y= - 3,n=2.解: yn(yn + 9y - 12) – 3(3yn+1 - 4yn)= y 2n+ 9yn+1- 12 yn– 9yn+1 +12 yn= y 2n当y= - 3,n=2时,原式=(- 3)4=81虞老师今年1月看中了杜桥蓝盾的一套房屋,为了想了解客厅的面积,用自己的步长(步长为a米)去测量客厅,量得客厅长15步,宽14步,请问客厅有多少平方米?请你帮忙:15a·14a=210a2 (m2)虞老师对刚才的那套房屋比较满意,决定购买后打算把除卧室以外的其它部分全都铺上地砖,问至少需要多少平方米的地转?
如果某种地转的价格是a元/平方米,那么购买地砖至少需要多少元?请你帮忙:4x· 2y+2x· y+x· y=8xy+2xy+xy=11xy11xy· a=11axy探索与思考解:ab(a2b5-ab3-b)=a3b6-a2b4-ab2=(ab2)3-(ab2)2-ab2当ab2=-6时,原式=( - 6)3 -( - 6)2- (- 6)=-2463、若(am+1bn+2)(a2n-1b2m)=a5b3 则m+n的值为 ( )(A) 1 (B)2 (C)3 (D) -3 BB挑战自我: 动脑筋: 计算下列图形的面积?方法1:=方法2:=方法3:方法4:ab-(a-t) (b-t)=at+bt-t23、计算:
(x + 1)( x2 – 2x + 3)
(x – 1)(x2 + x + 1)
(4x – 3)(5x2 – 4x + 7)
(3x + 2)(3x – 2)(x2 – 1)
(5) (3a – 2)(a – 1) + (a + 1)(a + 2)
(6) (2x2 – 1)(x – 4) - ( x2 + 3)(2x – 5)作业: 1、计算:
(1) (3x + 1)(x + 2) (2) (4y - 1)(y - 5)
(2x - 3)(4x - 1) (4) (3a +2)(4a + 1)
(5 ) (7x2 - 8y2)(x2 + 3y2) (6)(9m - 4n)(9m - 4n)
(7) (8) (x + 2)(x - 2)(x2 + 4)
(9) (1 - 2x + 4x2)(1 + 2x)
(x - y)(x2 + xy + y2)
(11) 5x(x2+2x +1) - (2x + 3)(x - 5)
(12) (3x – y)(y + 3x) - (4x - 3y)(3y + 4x)2、计算:
(1) (x + 3)(x + 2)
(2) (a + 5)(a - 3)
(3) (x - 5)(x + 3)
(4) (m + 2)(m - 8)
(5)先化简,再求值
(3x + 1)(2x - 3) - (6x - 5)(x - 4)
其中x = -2课时小结: 1、单项式与多项式相乘的实质是把单项式乘以多项式转化为单项式乘法 2、相关的混合运算,要弄清顺序
(1)单项式乘以单项式或单项式乘以多项式。
(2)整式加减注意最后应合并同类项。几点注意: 1、 单项式分别与多项式的每一项相乘时,要注意积的各项符号的确定:同号相乘得正,异号相乘得负 2.不要出现漏乘现象3、运算要有顺序:先乘方,再乘除,最后加减。有括号一般先去括号(小→大)转化思想单项式与单项式相乘的法则生活中处处有数学思想方法收获应用收获知识收获谈收获老师们、同学们、再见!
