整式的乘法_多项式乘以多项式[上学期]
文档属性
| 名称 | 整式的乘法_多项式乘以多项式[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-02 16:35:00 | ||
图片预览



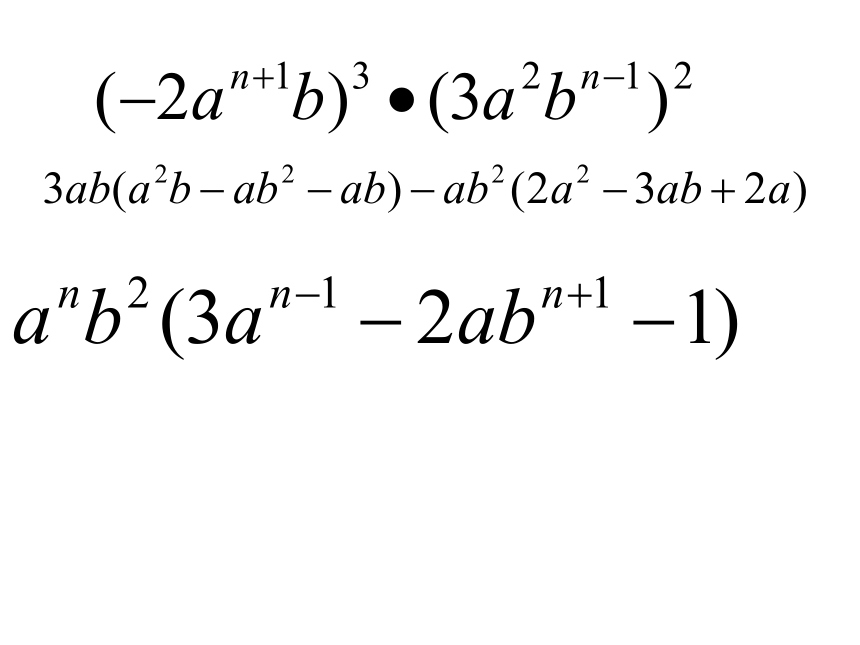


文档简介
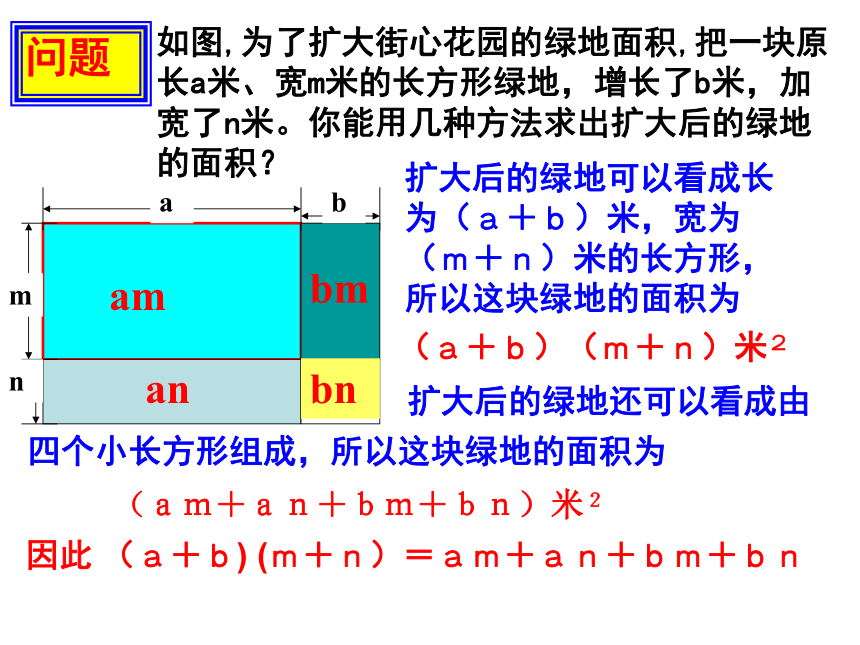
课件18张PPT。15.2.4 整式的乘法(一)复习提问?3、幂的乘方:4、积的乘方:2、同底数幂的乘法法则:其中 m , n都是正整数1、合并同类项:单项式与多项式相乘法则: 单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加。m(a+b+c)=ma+mb+mc问题如图,为了扩大街心花园的绿地面积,把一块原长a米、宽m米的长方形绿地,增长了b米,加宽了n米。你能用几种方法求出扩大后的绿地的面积?扩大后的绿地可以看成长为(a+b)米,宽为(m+n)米的长方形,所以这块绿地的面积为(a+b)(m+n)米2(am+an+bm+bn)米2ambmanbn因此 (a+b) (m+n)=am+an+bm+bn(a+b) (m+n)计算:(a+b) (m+n),可以先把其中的一个多项式,如(m+n),看成一个整体,运用单项式与多项式相乘的法则,得=a(m+n)+b(m+n)再利用单项式与多项式相乘的法则,得a(m+n)+b(m+n)=am+an+bm+bn 总体一看,(a+b) (m+n)的结果可以看作由a+b的每一项乘m+n的每一项,再把所得的积相加而得到的,即(a+b) (m+n)=am+an+bm+bn 多项式与多项式相乘,先用一个多项式的每一项乘另一多项式的每一项,再把所得的积相加。(a+b)(m+n)=am1234+an+bm+bn多项式的乘法法则例题解析 【例】计算: (1)(x+2)(x?3), (2)(3x -1)(2x+1)。?3x+2x=x2 -x-6 -2×3(2) (3x -1)(2x+1)=3x?2x+3x? 1-1?2 x?1=6x2+3x-2 x?1=6x2 +x?1. 【例】计算: (1)(x?3y)(x+7y), (2)(2x + 5y)(3x?2y)。+7xy?3yx-=x2 +4xy-21y2; 21y2(2) (2x +5 y)(3x?2y)==x22x?3x ?2x? 2y +5 y? 3x?5y?2y=6x2?4xy+ 15xy?10y2=6x2 +11xy?10y2.例、计算:
(1)(3x + 1)(x - 2) (2) (x – 8y)(x – y)解: (1) (3x + 1)(x - 2)=(3x) ·x + (3x) ·(-2) +1·x + 1×(-2)=3x2 – 6x + x - 2=3x2 – 5x - 2(2) (x – 8y)(x – y)= x2 – xy – 8xy + 8y2= x2 – 9xy + 8y23、计算:
(x + 1)( x2 – 2x + 3)
(3x + 2)(3x – 2)(x2 – 1)
(6) (2x2 – 1)(x – 4) - ( x2 + 3)(2x – 5)
方法与规律延伸训练:填空:观察上面四个等式,你能发现什么规律?你能根据这个规律解决下面的问题吗?计算、观察、找规律:归纳2、计算:
(1) (x + 3)(x + 2)
(2) (a + 5)(a - 3)
(3) (x - 5)(x + 3)
(4) (m + 2)(m - 8)
(5)先化简,再求值
(3x + 1)(2x - 3) - (6x - 5)(x - 4)
其中x = -2挑战极限: 如果(x2+bx+8)(x2 – 3x+c)的乘积中不含x2和x3的项,求b、c的值。解:原式= x4 – 3x3 + c x2 +bx3
– 3bx2 +bcx+8 x2– 24x+8cX2项系数为:c –3b+8X3项系数为:b – 3= 0= 0∴ b=3 , c=1拓展与提高谢谢再见别忘了完成作业哦!
(1)(3x + 1)(x - 2) (2) (x – 8y)(x – y)解: (1) (3x + 1)(x - 2)=(3x) ·x + (3x) ·(-2) +1·x + 1×(-2)=3x2 – 6x + x - 2=3x2 – 5x - 2(2) (x – 8y)(x – y)= x2 – xy – 8xy + 8y2= x2 – 9xy + 8y23、计算:
(x + 1)( x2 – 2x + 3)
(3x + 2)(3x – 2)(x2 – 1)
(6) (2x2 – 1)(x – 4) - ( x2 + 3)(2x – 5)
方法与规律延伸训练:填空:观察上面四个等式,你能发现什么规律?你能根据这个规律解决下面的问题吗?计算、观察、找规律:归纳2、计算:
(1) (x + 3)(x + 2)
(2) (a + 5)(a - 3)
(3) (x - 5)(x + 3)
(4) (m + 2)(m - 8)
(5)先化简,再求值
(3x + 1)(2x - 3) - (6x - 5)(x - 4)
其中x = -2挑战极限: 如果(x2+bx+8)(x2 – 3x+c)的乘积中不含x2和x3的项,求b、c的值。解:原式= x4 – 3x3 + c x2 +bx3
– 3bx2 +bcx+8 x2– 24x+8cX2项系数为:c –3b+8X3项系数为:b – 3= 0= 0∴ b=3 , c=1拓展与提高谢谢再见别忘了完成作业哦!
