2022-2023学年北师大版数学七年级上册第3章 整式及其加减 综合测试卷(含答案)
文档属性
| 名称 | 2022-2023学年北师大版数学七年级上册第3章 整式及其加减 综合测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 397.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-24 00:00:00 | ||
图片预览




文档简介
第3章 整式及其加减 综合测试卷
一、单选题
1.下列各组两项属于同类项的是( )
A.与 B.和 C.和 D.2与
2.下列各式:﹣mn,m,8,,x2+2x+6,,,y3﹣5y+中,整式有( )
A.3个 B.4个 C.6个 D.7个
3.代数式, 2x+y, a2b, , , 0.5 中整式的个数( )
A.3个 B.4个 C.5个 D.6个
4.下面是小芳做的一道多项式的加减运算题,但她不小心把一滴墨水滴在了上面: ,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是( )
A. B. C. D.
5.在式子,,,,,,中,单项式有( )
A.3个 B.4个 C.5个 D.6个
6.乐乐在数学学习中遇到了神奇的“数值转换机”,按如图所示的程序运算,若输入一个有理数,则可相应的输出一个结果.若输入的值为,则输出的结果为( )
A. B. C. D.
7.小李今年a岁,小王今年(a-15)岁,过n+1年后,他们相差( )岁
A.15 B.n+1 C.n+16 D.16
8.已知关于x、y的多项式合并后不含有二次项,则m+n的值为( )
A.-5 B.-1 C.1 D.5
9.将从1开始的连续奇数按如图所示的规律排列,例如,位于第4行第3列的数为27,则位于第32行第13列的数是( )
A.2025 B.2023 C.2021 D.2019
10.已知与是同类项,则的值是( )
A.2 B.3 C.4 D.5
11.如图,将图1中的长方形纸片前成①号、②号、③号、④号正方形和⑤号长方形,并将它们按图2的方式无重叠地放入另一个大长方形中,若需求出没有覆盖的阴影部分的周长,则下列说法中错误的是( )
A.只需知道图1中大长方形的周长即可
B.只需知道图2中大长方形的周长即可
C.只需知道③号正方形的周长即可
D.只需知道⑤号长方形的周长即可
12.多项式与多项式相加后,不含二次项,则常数m的值是( )
A.2 B. C. D.
13.数学家华罗庚曾经说过:“数形结合百般好,隔裂分家万事休”.如图,将一个边长为1的正方形纸板等分成两个面积为的长方形,接着把面积为的长方形分成两个面积为的长方形,如此继续进行下去,根据图形的规律计算:的值为( )
A. B. C. D.
14.2020年我省财政收入比2019年增长8.9%,2021年比2020年增长9.5%,若2019年和2021年我省财政收入分别为a亿元和b亿元,则a、b之间满足的关系式为( )
A. B.
C. D.
15.已知:关于,的多项式不含二次项,则的值是( )
A.-3 B.2 C.-17 D.18
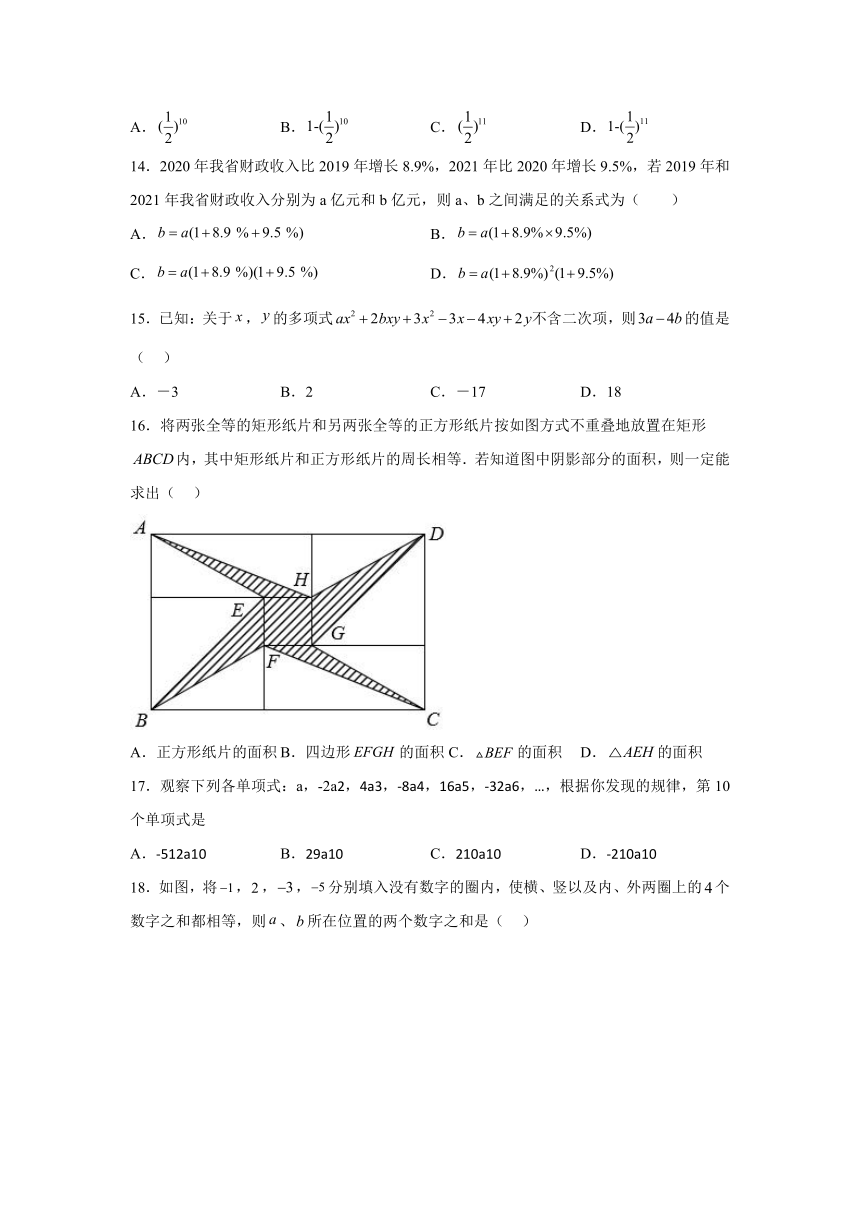
16.将两张全等的矩形纸片和另两张全等的正方形纸片按如图方式不重叠地放置在矩形内,其中矩形纸片和正方形纸片的周长相等.若知道图中阴影部分的面积,则一定能求出( )
A.正方形纸片的面积 B.四边形的面积C.的面积 D.的面积
17.观察下列各单项式:a,-2a2,4a3,-8a4,16a5,-32a6,…,根据你发现的规律,第10个单项式是
A.-512a10 B.29a10 C.210a10 D.-210a10
18.如图,将,,,分别填入没有数字的圈内,使横、竖以及内、外两圈上的个数字之和都相等,则、所在位置的两个数字之和是( )
A.或 B.或 C.或 D.或.
19.定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
若n=13,则第2018次“F”运算的结果是( )
A.1 B.4 C.2018 D.42018
20.2018年电影《我不是药神》反映了进口药用药贵的事实,从而引起了社会的广泛关注.国家针对部分药品进行改革,看病贵将成为历史.某药厂对售价为m元的药品进行了降价,现在有三种方案.
方案一:第一次降价10%,第二次降价30%;
方案二:第一次降价20%,第二次降价15%;
方案三:第一、二次降价均为20%.三种方案哪种降价最多( )
A.方案一 B.方案二 C.方案三 D.不能确定
二、填空题
21.如将看成一个整体,则化简多项式__.
22.若代数式的值与字母无关,则的值为__________.
23.将黑色圆点按如图所示的规律进行排列,图中黑色圆点的个数依次为:1,3,6,10,……,将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据,则新数据中的第33个数为___________.
24.-_________________=.
25.观察下列一组数:2,,,…,它们按一定规律排列,第n个数记为,且满足.则________,________.
三、解答题
26.计算
(1)
(2)
(3)2x+3y-2(3x-y);
(4).
(5)
(6)
27.阅读材料:数学活动课上,小智同学提出一个猜想;把一个三位正整数的百位上的与个位上的数交换位置,十位上的数不变,原数与所得数的差等于99乘原数的百位上的数与个位上的数的差.例如:782﹣287=99×(7﹣2).
(1)小智的猜想是否正确?若正确,对任意情况进行说明;若不正确,说明理由.
(2)已知一个五位正整数的万位上的数为m,个位上的数为n,把万位上的数与个位上的数交换位置,其余数位上的数不变,原数与所得数的差等于 .(用含m,n的式子表示)
28.若一个四位数正整数,其千位数字的5倍与后三位组成的数的和得到的数称为t的“笃学数”,记为,“笃学数”百位数字的5倍与后两位组成的数的和得到的数称为t的“图新数”,记为,例如:3412的“笃学数”为,3412的“图新数”,
(1)写______;______;
(2)若一个千位为4,十位为6的四位数的“笃学数”与“图新数”之和能被33整除,求该四位数.
29.已知多项式的常数项是a,次数是b,a、b在数轴上分别表示的点是A、B(如图),点A与点B之间的距离记作.
(1)求a,b的值;
(2)动点P从数1对应的点开始向右运动,速度为每秒1个单位长度.同时点A,B在数轴上运动,点A,B的速度分别为每秒2个单位长度,每秒3个单位长度,运动时间为t秒.
①若点A向右运动,点B向左运动,,求t的值;
②若点A向左运动,点B向右运动,问是否存在常数m,使得的值为定值?若存在,求出m的值,且定值为多少?若不存在,说明理由.
30.阅读探究:,,,…
(1)根据上述规律,小亮发现,求出___________.
(2)小聪继续又发现:
,求出___________.
若,请运用小聪的方法求和的值。
参考答案
1--10DCBDB BACBB 11--20BBBCC CABAA
21.
22.-2
23.1275
24.
25.
26.解:(1)原式=﹣a2b+3ab2﹣a2b﹣4ab2+2a2b
=(﹣1﹣1+2)a2b+(3﹣4)ab2
=﹣ab2,
(2)原式=3x2y﹣xy+3xy2﹣(2xy2 - 2xy +3x2y)
=3x2y﹣xy+3xy2﹣2xy2 +2xy-3x2y
=xy2+xy,
(3)解:原式=2x+3y-6x+2y
=-4x+5y.
(4)解:原式
.
(5)解:
=
=2x-3y;
(6)解:
=
= m2-3m
27.(1)解:小智的猜想正确.证明如下:
设一个三位正整数的百位上的数为a,十位上的数为b,个位上的数为c,则
该三位正整数为100a+10b+c,新三位正整数为100c+10b+a,
因为100a+10b+c﹣(100c+10b+a)
=100a+10b+c﹣100c﹣10b﹣a
=99a﹣99c
=99(a﹣c),
所以小智的猜想是正确的;
(2)
解:原数与所得数的差等于10000m+n﹣(10000n+m)=10000m+n﹣10000n﹣m=9999m﹣9999n=9999(m﹣n).
故答案为:9999(m﹣n).
28.(1),
.
故答案为:264,74;
(2)设这个四位数为4a6b(,且a、b为整数 )
则,
.
∴.
∵能被33整除,且,a、b为整数.
∴①当时,即能被33整除,得不符合题意;
②当时,即能被33整除,得不符合题意;
③当时,即能被33整除,得不符合题意;
④当时,即能被33整除,得不符合题意;
⑤当时,即能被33整除,得符合题意;
⑥当时,即能被33整除,得符合题意;
⑦当时,即能被33整除,得符合题意;
⑧当时,即能被33整除,得不符合题意;
⑨当时,即能被33整除,得不符合题意;
⑩当时,即能被33整除,得不符合题意.
综上可知,这个四位数为4467或4564或4661.
29.(1)解∶∵多项式的常数项是-20,次数是30.
∴a=-20,b=30;
(2)
解:①如下图所示∶
当t=0时,AP=21,BP=29,
若点A向右运动,点B向左运动,则运动t秒时,A点表示的数为-20+2t,B点表示的数为30-3t.
∵动点P从数1对应的点开始向右运动,速度为每秒1个单位长度,
∴运动t秒时,P点表示的数为1+t;
下面分两类情况来讨论∶点A、B在相遇前时,
∵AP=PB,
∴1+t-(-20+2t)=30-3t-(1+t),
解得;
点A、B在相遇时,AP=PB,此时A与B重台,
则-20+2t=30-3t,解得t=10;
显然,点A,B在相遇后,BP大于AP,不符合条件.
综上所述,或10;
②当运动t秒时,A点表示的数为-20-2t,B点表示的数为30+3t,P点表示的数为1+t,
2AP-m×PB
=2[(1+t)-(-20-2t)]-m[(30+3t)-(1+t)]
=(6-2m)t+(42-29m),
当6-2m=0时,上式的值不随时间t的变化而改变.
∴存在常数m=3,使得的值为定值,此时.
30.(1)解:∵,,,
∴,
∴
故答案为:6
(2)
解:∵,
,
∴,
∴.
故答案为:7
(3)
解:∵,
∴
∵,
∴,.
一、单选题
1.下列各组两项属于同类项的是( )
A.与 B.和 C.和 D.2与
2.下列各式:﹣mn,m,8,,x2+2x+6,,,y3﹣5y+中,整式有( )
A.3个 B.4个 C.6个 D.7个
3.代数式, 2x+y, a2b, , , 0.5 中整式的个数( )
A.3个 B.4个 C.5个 D.6个
4.下面是小芳做的一道多项式的加减运算题,但她不小心把一滴墨水滴在了上面: ,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是( )
A. B. C. D.
5.在式子,,,,,,中,单项式有( )
A.3个 B.4个 C.5个 D.6个
6.乐乐在数学学习中遇到了神奇的“数值转换机”,按如图所示的程序运算,若输入一个有理数,则可相应的输出一个结果.若输入的值为,则输出的结果为( )
A. B. C. D.
7.小李今年a岁,小王今年(a-15)岁,过n+1年后,他们相差( )岁
A.15 B.n+1 C.n+16 D.16
8.已知关于x、y的多项式合并后不含有二次项,则m+n的值为( )
A.-5 B.-1 C.1 D.5
9.将从1开始的连续奇数按如图所示的规律排列,例如,位于第4行第3列的数为27,则位于第32行第13列的数是( )
A.2025 B.2023 C.2021 D.2019
10.已知与是同类项,则的值是( )
A.2 B.3 C.4 D.5
11.如图,将图1中的长方形纸片前成①号、②号、③号、④号正方形和⑤号长方形,并将它们按图2的方式无重叠地放入另一个大长方形中,若需求出没有覆盖的阴影部分的周长,则下列说法中错误的是( )
A.只需知道图1中大长方形的周长即可
B.只需知道图2中大长方形的周长即可
C.只需知道③号正方形的周长即可
D.只需知道⑤号长方形的周长即可
12.多项式与多项式相加后,不含二次项,则常数m的值是( )
A.2 B. C. D.
13.数学家华罗庚曾经说过:“数形结合百般好,隔裂分家万事休”.如图,将一个边长为1的正方形纸板等分成两个面积为的长方形,接着把面积为的长方形分成两个面积为的长方形,如此继续进行下去,根据图形的规律计算:的值为( )
A. B. C. D.
14.2020年我省财政收入比2019年增长8.9%,2021年比2020年增长9.5%,若2019年和2021年我省财政收入分别为a亿元和b亿元,则a、b之间满足的关系式为( )
A. B.
C. D.
15.已知:关于,的多项式不含二次项,则的值是( )
A.-3 B.2 C.-17 D.18
16.将两张全等的矩形纸片和另两张全等的正方形纸片按如图方式不重叠地放置在矩形内,其中矩形纸片和正方形纸片的周长相等.若知道图中阴影部分的面积,则一定能求出( )
A.正方形纸片的面积 B.四边形的面积C.的面积 D.的面积
17.观察下列各单项式:a,-2a2,4a3,-8a4,16a5,-32a6,…,根据你发现的规律,第10个单项式是
A.-512a10 B.29a10 C.210a10 D.-210a10
18.如图,将,,,分别填入没有数字的圈内,使横、竖以及内、外两圈上的个数字之和都相等,则、所在位置的两个数字之和是( )
A.或 B.或 C.或 D.或.
19.定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
若n=13,则第2018次“F”运算的结果是( )
A.1 B.4 C.2018 D.42018
20.2018年电影《我不是药神》反映了进口药用药贵的事实,从而引起了社会的广泛关注.国家针对部分药品进行改革,看病贵将成为历史.某药厂对售价为m元的药品进行了降价,现在有三种方案.
方案一:第一次降价10%,第二次降价30%;
方案二:第一次降价20%,第二次降价15%;
方案三:第一、二次降价均为20%.三种方案哪种降价最多( )
A.方案一 B.方案二 C.方案三 D.不能确定
二、填空题
21.如将看成一个整体,则化简多项式__.
22.若代数式的值与字母无关,则的值为__________.
23.将黑色圆点按如图所示的规律进行排列,图中黑色圆点的个数依次为:1,3,6,10,……,将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据,则新数据中的第33个数为___________.
24.-_________________=.
25.观察下列一组数:2,,,…,它们按一定规律排列,第n个数记为,且满足.则________,________.
三、解答题
26.计算
(1)
(2)
(3)2x+3y-2(3x-y);
(4).
(5)
(6)
27.阅读材料:数学活动课上,小智同学提出一个猜想;把一个三位正整数的百位上的与个位上的数交换位置,十位上的数不变,原数与所得数的差等于99乘原数的百位上的数与个位上的数的差.例如:782﹣287=99×(7﹣2).
(1)小智的猜想是否正确?若正确,对任意情况进行说明;若不正确,说明理由.
(2)已知一个五位正整数的万位上的数为m,个位上的数为n,把万位上的数与个位上的数交换位置,其余数位上的数不变,原数与所得数的差等于 .(用含m,n的式子表示)
28.若一个四位数正整数,其千位数字的5倍与后三位组成的数的和得到的数称为t的“笃学数”,记为,“笃学数”百位数字的5倍与后两位组成的数的和得到的数称为t的“图新数”,记为,例如:3412的“笃学数”为,3412的“图新数”,
(1)写______;______;
(2)若一个千位为4,十位为6的四位数的“笃学数”与“图新数”之和能被33整除,求该四位数.
29.已知多项式的常数项是a,次数是b,a、b在数轴上分别表示的点是A、B(如图),点A与点B之间的距离记作.
(1)求a,b的值;
(2)动点P从数1对应的点开始向右运动,速度为每秒1个单位长度.同时点A,B在数轴上运动,点A,B的速度分别为每秒2个单位长度,每秒3个单位长度,运动时间为t秒.
①若点A向右运动,点B向左运动,,求t的值;
②若点A向左运动,点B向右运动,问是否存在常数m,使得的值为定值?若存在,求出m的值,且定值为多少?若不存在,说明理由.
30.阅读探究:,,,…
(1)根据上述规律,小亮发现,求出___________.
(2)小聪继续又发现:
,求出___________.
若,请运用小聪的方法求和的值。
参考答案
1--10DCBDB BACBB 11--20BBBCC CABAA
21.
22.-2
23.1275
24.
25.
26.解:(1)原式=﹣a2b+3ab2﹣a2b﹣4ab2+2a2b
=(﹣1﹣1+2)a2b+(3﹣4)ab2
=﹣ab2,
(2)原式=3x2y﹣xy+3xy2﹣(2xy2 - 2xy +3x2y)
=3x2y﹣xy+3xy2﹣2xy2 +2xy-3x2y
=xy2+xy,
(3)解:原式=2x+3y-6x+2y
=-4x+5y.
(4)解:原式
.
(5)解:
=
=2x-3y;
(6)解:
=
= m2-3m
27.(1)解:小智的猜想正确.证明如下:
设一个三位正整数的百位上的数为a,十位上的数为b,个位上的数为c,则
该三位正整数为100a+10b+c,新三位正整数为100c+10b+a,
因为100a+10b+c﹣(100c+10b+a)
=100a+10b+c﹣100c﹣10b﹣a
=99a﹣99c
=99(a﹣c),
所以小智的猜想是正确的;
(2)
解:原数与所得数的差等于10000m+n﹣(10000n+m)=10000m+n﹣10000n﹣m=9999m﹣9999n=9999(m﹣n).
故答案为:9999(m﹣n).
28.(1),
.
故答案为:264,74;
(2)设这个四位数为4a6b(,且a、b为整数 )
则,
.
∴.
∵能被33整除,且,a、b为整数.
∴①当时,即能被33整除,得不符合题意;
②当时,即能被33整除,得不符合题意;
③当时,即能被33整除,得不符合题意;
④当时,即能被33整除,得不符合题意;
⑤当时,即能被33整除,得符合题意;
⑥当时,即能被33整除,得符合题意;
⑦当时,即能被33整除,得符合题意;
⑧当时,即能被33整除,得不符合题意;
⑨当时,即能被33整除,得不符合题意;
⑩当时,即能被33整除,得不符合题意.
综上可知,这个四位数为4467或4564或4661.
29.(1)解∶∵多项式的常数项是-20,次数是30.
∴a=-20,b=30;
(2)
解:①如下图所示∶
当t=0时,AP=21,BP=29,
若点A向右运动,点B向左运动,则运动t秒时,A点表示的数为-20+2t,B点表示的数为30-3t.
∵动点P从数1对应的点开始向右运动,速度为每秒1个单位长度,
∴运动t秒时,P点表示的数为1+t;
下面分两类情况来讨论∶点A、B在相遇前时,
∵AP=PB,
∴1+t-(-20+2t)=30-3t-(1+t),
解得;
点A、B在相遇时,AP=PB,此时A与B重台,
则-20+2t=30-3t,解得t=10;
显然,点A,B在相遇后,BP大于AP,不符合条件.
综上所述,或10;
②当运动t秒时,A点表示的数为-20-2t,B点表示的数为30+3t,P点表示的数为1+t,
2AP-m×PB
=2[(1+t)-(-20-2t)]-m[(30+3t)-(1+t)]
=(6-2m)t+(42-29m),
当6-2m=0时,上式的值不随时间t的变化而改变.
∴存在常数m=3,使得的值为定值,此时.
30.(1)解:∵,,,
∴,
∴
故答案为:6
(2)
解:∵,
,
∴,
∴.
故答案为:7
(3)
解:∵,
∴
∵,
∴,.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
