华师大版数学九年级上册 25.1.2 频数与频率 课件(共21张PPT)
文档属性
| 名称 | 华师大版数学九年级上册 25.1.2 频数与频率 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 881.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-24 00:00:00 | ||
图片预览


文档简介
(共22张PPT)
第二十五章 随机事件的概率
25.1 在重复试验中观察不确定现象
第2课时 频数与频率
1
课堂讲解
频数和频率
在重复实验中观察不确定现象
2
课时流程
逐点
导讲练
课堂小结
作业提升
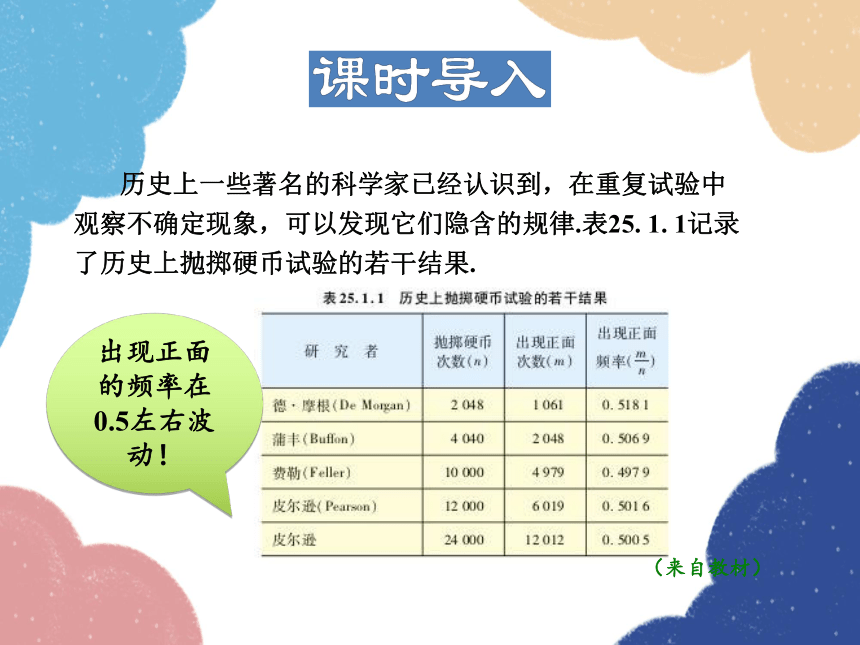
历史上一些著名的科学家已经认识到,在重复试验中观察不确定现象,可以发现它们隐含的规律.表25. 1. 1记录了历史上抛掷硬币试验的若干结果.
(来自教材)
出现正面的频率在0.5左右波动!
1
知识点
频数和频率
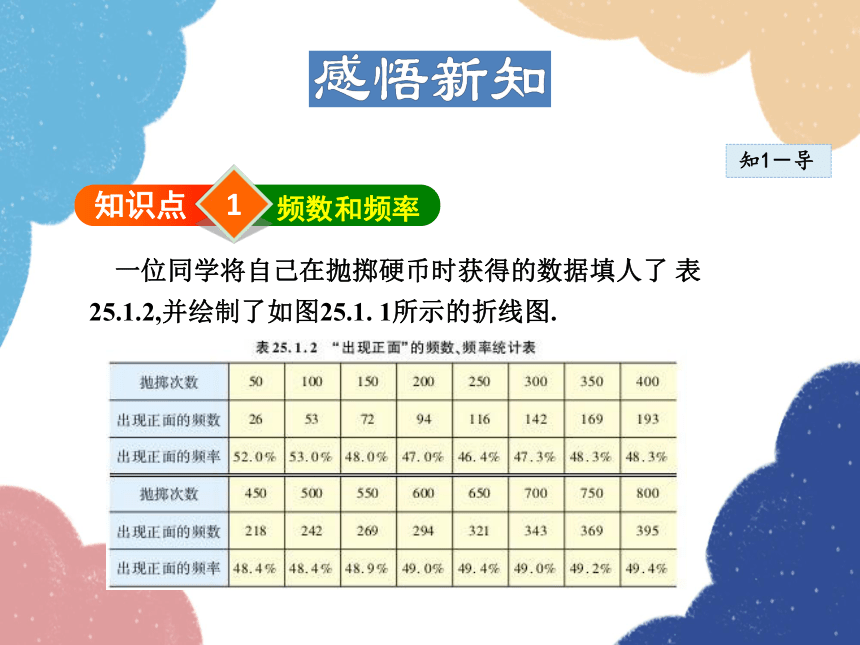
一位同学将自己在抛掷硬币时获得的数据填人了 表25.1.2,并绘制了如图25.1. 1所示的折线图.
知1-导
知1-导
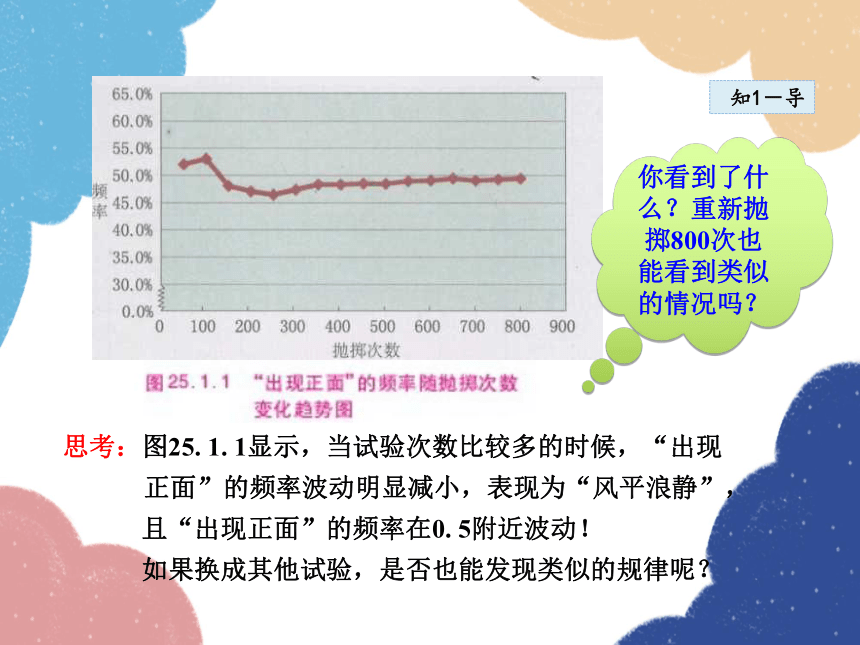
思考:图25. 1. 1显示,当试验次数比较多的时候,“出现
正面”的频率波动明显减小,表现为“风平浪静”,
且“出现正面”的频率在0. 5附近波动!
如果换成其他试验,是否也能发现类似的规律呢?
你看到了什么?重新抛掷800次也能看到类似的情况吗?
知1-讲
概括: 在前面的试验中,我们可以发现,虽然每次试验
的结果是随机的,无法预测,但随着试验次数的增加,隐含的规律逐渐显现,事件发生的频率会稳定到某一个数值附近.正因为随机现象发生的频率有这样趋于稳定的特点,所以我们就可以用频率估计随机事件在每次试验时发 生的机会的大小.
(来自《教材》)
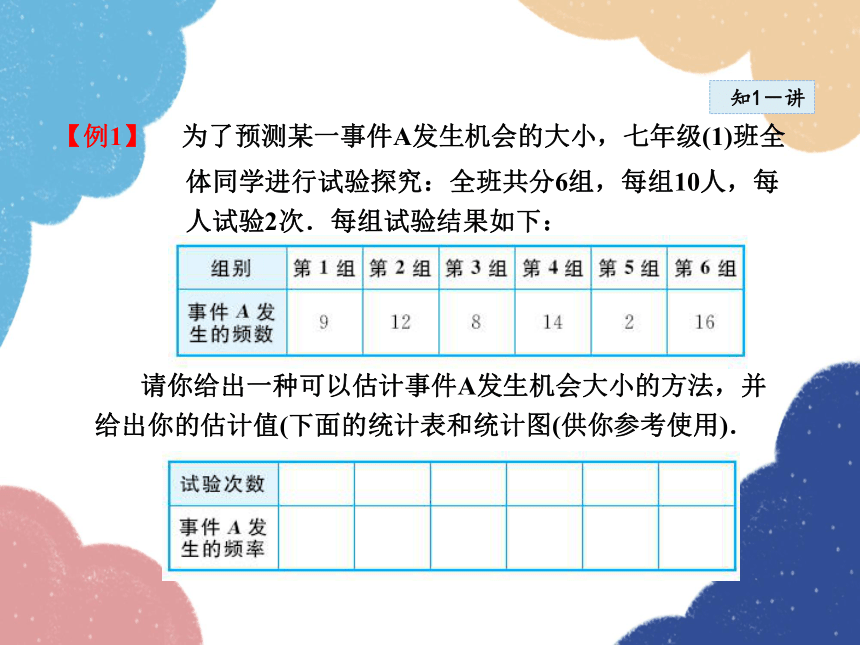
【例1】 为了预测某一事件A发生机会的大小,七年级(1)班全
体同学进行试验探究:全班共分6组,每组10人,每人试验2次.每组试验结果如下:
知1-讲
请你给出一种可以估计事件A发生机会大小的方法,并给出你的估计值(下面的统计表和统计图(供你参考使用).
知1-讲
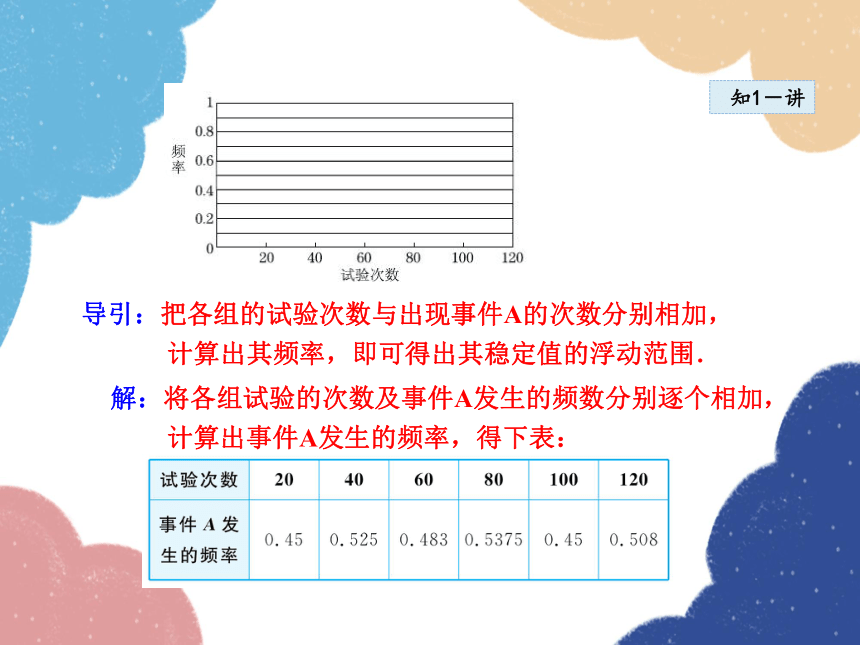
解:将各组试验的次数及事件A发生的频数分别逐个相加,
计算出事件A发生的频率,得下表:
导引:把各组的试验次数与出现事件A的次数分别相加,
计算出其频率,即可得出其稳定值的浮动范围.
知1-讲
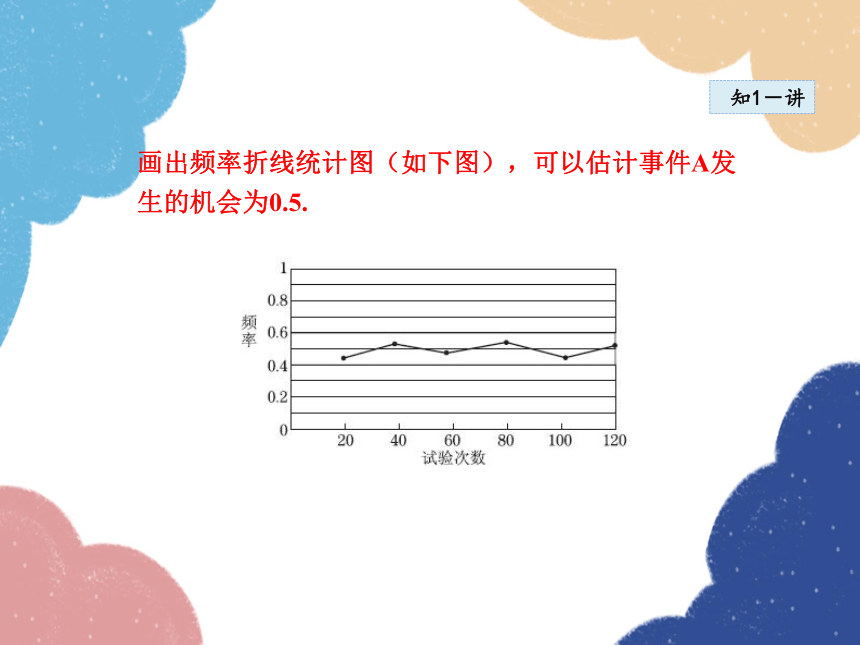
画出频率折线统计图(如下图),可以估计事件A发生的机会为0.5.
知1-讲
总 结
本题是一道开放性问题,重在估计方法的设计,答案不唯一.如试验次数累加的次序不同,则表中“事件A发生的频率”就会出现不同的数值,折线图也就不一样了.
某人在一次抛掷硬币的试验中,结果为“正面朝上”的频数为52,频率为40%,此人共拋掷了________次.
知1-练
九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布
直方图(满分为30分,成绩均为
整数).若将不低于23分的成绩
评为合格,则该班此次成绩达到
合格的同学占全班人数的百分比
是 .
2
知识点
在重复实验中观察不确定现象
知2-导
读一读
由此,我们可以体会到:开展重复试验活动(如同时抛掷两枚硬币)时,虽然每次收集到的数据(如出现哪两个面)可能会是不同的,但通过大量的重复试验,就可能从中发现规律(如出现两个正面的频率稳定在25%附近)
我们可以借助数据分析,认识随机事件发生的规律
(来自教材)
知2-讲
1. 在试验中,虽然每次试验的结果都是随机、无法预测的,但随着试验次数的增加,隐含的规律逐渐显现,事件发生的频率会稳定到某一个数值附近.这个稳定值就可以作为该事件在每次试验中发生的可能性大小的一个估计值.
2.某些随机事件是无法用公式计算解决和主观臆造的,试验是预测某些随机事件发生可能性的必要手段.
【例2】 七年级(1)班同学做抛硬币的试验,每人10次,5人,
10人, 15人,…,50人的试验数据如下表:
知2-讲
(1) 填空:a1=______;a2=______;a3=________;
a4=________;
知2-讲
(2)在图25.1 3中画出正面朝上的频率折线统计图;
(3)估计正面朝上的机会是________.
知2-讲
导引:(1) 由频率=频数÷试验次数算出频率;
(2) 根据表格绘制频率折线统计图;
(3) 根据折线图观察随着抛掷次数的增多,正面朝
上的频率稳定到哪 个数值,该数值即可作为正
面朝上机会的估计值.
知2-讲
解:(1) 0.49;0.52;0.505;0.488
(2) 如图25.1 4.
(3) 0.5
知2-讲
总 结
大量重复试验下频率稳定在一个数值附近.我们可以用频率估计随机事件在每次试验时发生的机会的大小.
知2-练
1 某种绿豆在相同条件下发芽的试验结果如下表,根据表中数据估计这种绿豆发芽的机会大约是________(精确到0.01).
从n个苹果和3个雪梨中任选1个,若选中苹果的机会是
则n的值是( )
A.6 B.3 C.2 D.1
知2-练
2 某灯泡厂的一次质量检查,从2 000个灯泡中抽查了100个,其中有6个不合格,则出现不合格产品的频率为________,在这2 000个灯泡中,估计有________个不合格产品.
用频率估计随机事件发生的机会的大小的方法:利用频率估计随机事件发生的机会的大小时,不能以某一次试验的结果作为估计的随机事件发生的机会的大小.试验的次数越多,用频率估计也越准确,因此用多次试验后的频率的稳定值估计随机事件发生的机会的大小.
第二十五章 随机事件的概率
25.1 在重复试验中观察不确定现象
第2课时 频数与频率
1
课堂讲解
频数和频率
在重复实验中观察不确定现象
2
课时流程
逐点
导讲练
课堂小结
作业提升
历史上一些著名的科学家已经认识到,在重复试验中观察不确定现象,可以发现它们隐含的规律.表25. 1. 1记录了历史上抛掷硬币试验的若干结果.
(来自教材)
出现正面的频率在0.5左右波动!
1
知识点
频数和频率
一位同学将自己在抛掷硬币时获得的数据填人了 表25.1.2,并绘制了如图25.1. 1所示的折线图.
知1-导
知1-导
思考:图25. 1. 1显示,当试验次数比较多的时候,“出现
正面”的频率波动明显减小,表现为“风平浪静”,
且“出现正面”的频率在0. 5附近波动!
如果换成其他试验,是否也能发现类似的规律呢?
你看到了什么?重新抛掷800次也能看到类似的情况吗?
知1-讲
概括: 在前面的试验中,我们可以发现,虽然每次试验
的结果是随机的,无法预测,但随着试验次数的增加,隐含的规律逐渐显现,事件发生的频率会稳定到某一个数值附近.正因为随机现象发生的频率有这样趋于稳定的特点,所以我们就可以用频率估计随机事件在每次试验时发 生的机会的大小.
(来自《教材》)
【例1】 为了预测某一事件A发生机会的大小,七年级(1)班全
体同学进行试验探究:全班共分6组,每组10人,每人试验2次.每组试验结果如下:
知1-讲
请你给出一种可以估计事件A发生机会大小的方法,并给出你的估计值(下面的统计表和统计图(供你参考使用).
知1-讲
解:将各组试验的次数及事件A发生的频数分别逐个相加,
计算出事件A发生的频率,得下表:
导引:把各组的试验次数与出现事件A的次数分别相加,
计算出其频率,即可得出其稳定值的浮动范围.
知1-讲
画出频率折线统计图(如下图),可以估计事件A发生的机会为0.5.
知1-讲
总 结
本题是一道开放性问题,重在估计方法的设计,答案不唯一.如试验次数累加的次序不同,则表中“事件A发生的频率”就会出现不同的数值,折线图也就不一样了.
某人在一次抛掷硬币的试验中,结果为“正面朝上”的频数为52,频率为40%,此人共拋掷了________次.
知1-练
九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布
直方图(满分为30分,成绩均为
整数).若将不低于23分的成绩
评为合格,则该班此次成绩达到
合格的同学占全班人数的百分比
是 .
2
知识点
在重复实验中观察不确定现象
知2-导
读一读
由此,我们可以体会到:开展重复试验活动(如同时抛掷两枚硬币)时,虽然每次收集到的数据(如出现哪两个面)可能会是不同的,但通过大量的重复试验,就可能从中发现规律(如出现两个正面的频率稳定在25%附近)
我们可以借助数据分析,认识随机事件发生的规律
(来自教材)
知2-讲
1. 在试验中,虽然每次试验的结果都是随机、无法预测的,但随着试验次数的增加,隐含的规律逐渐显现,事件发生的频率会稳定到某一个数值附近.这个稳定值就可以作为该事件在每次试验中发生的可能性大小的一个估计值.
2.某些随机事件是无法用公式计算解决和主观臆造的,试验是预测某些随机事件发生可能性的必要手段.
【例2】 七年级(1)班同学做抛硬币的试验,每人10次,5人,
10人, 15人,…,50人的试验数据如下表:
知2-讲
(1) 填空:a1=______;a2=______;a3=________;
a4=________;
知2-讲
(2)在图25.1 3中画出正面朝上的频率折线统计图;
(3)估计正面朝上的机会是________.
知2-讲
导引:(1) 由频率=频数÷试验次数算出频率;
(2) 根据表格绘制频率折线统计图;
(3) 根据折线图观察随着抛掷次数的增多,正面朝
上的频率稳定到哪 个数值,该数值即可作为正
面朝上机会的估计值.
知2-讲
解:(1) 0.49;0.52;0.505;0.488
(2) 如图25.1 4.
(3) 0.5
知2-讲
总 结
大量重复试验下频率稳定在一个数值附近.我们可以用频率估计随机事件在每次试验时发生的机会的大小.
知2-练
1 某种绿豆在相同条件下发芽的试验结果如下表,根据表中数据估计这种绿豆发芽的机会大约是________(精确到0.01).
从n个苹果和3个雪梨中任选1个,若选中苹果的机会是
则n的值是( )
A.6 B.3 C.2 D.1
知2-练
2 某灯泡厂的一次质量检查,从2 000个灯泡中抽查了100个,其中有6个不合格,则出现不合格产品的频率为________,在这2 000个灯泡中,估计有________个不合格产品.
用频率估计随机事件发生的机会的大小的方法:利用频率估计随机事件发生的机会的大小时,不能以某一次试验的结果作为估计的随机事件发生的机会的大小.试验的次数越多,用频率估计也越准确,因此用多次试验后的频率的稳定值估计随机事件发生的机会的大小.
