3.2合并同类项与移项(第4课时) 课件
文档属性
| 名称 | 3.2合并同类项与移项(第4课时) 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-16 10:32:45 | ||
图片预览





文档简介
课件14张PPT。人教版七年级数学上册
第三章一元一次方程3.2合并同类项与移项(第4课时)朱河镇初级中学七年级数学组本课内容掌握题目中含有比的应用题设未知数的方法建立方程解决实际问题 解下列方程 1、某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200t;如用新工艺,则废水排量比环保限制的最大值少100t.新旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少?思考下列问题:
(1)如果设新工艺废水排量是x吨,则旧工艺废水排量是 吨;
(2)如果设旧工艺废水排量是x吨,则新工艺废水排量是 吨;
(3)由新旧工艺的废水排量比是2:5,我们能否设新、旧工艺的废水排量是2x吨和3x吨?
(4)比较上述几种设未知数的方法,你觉得哪种方法更简单?
(5)题目中的等量关系是根据什么来确定的?环保限制的最大量如何表示?能(3)根据环保限制的最大量的不同表示关系列方程解:设新、旧工艺的废水排量分别为2x吨和3x吨,根据题意,得
5x-200=2x+100
移项,得 5x-2x=100+200
合并同类项,得 3x=300
系数化为1,得 x=100
所以, 2x=200, 5x=500
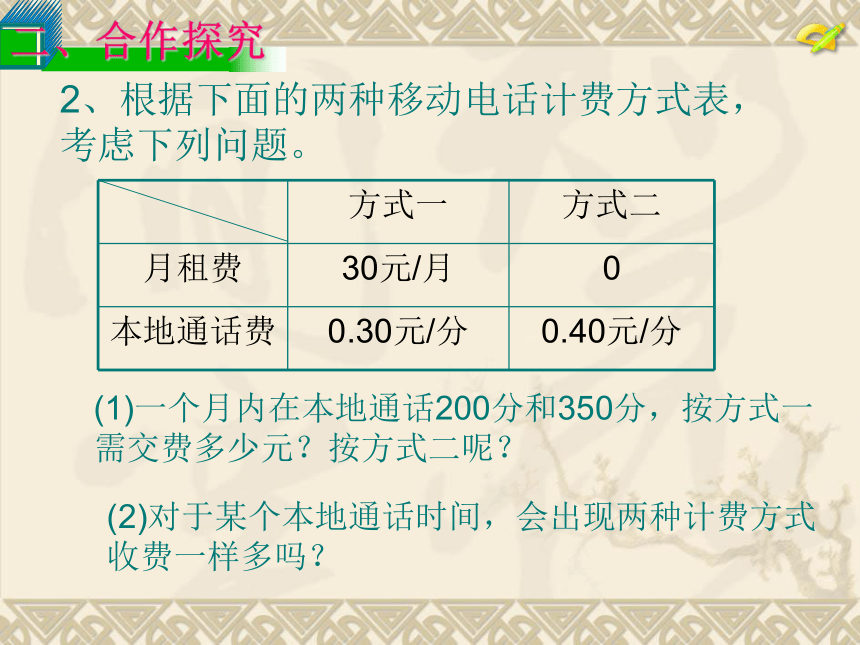
答:新、旧工艺产生的废水排量分别是200t和500t.2、根据下面的两种移动电话计费方式表,
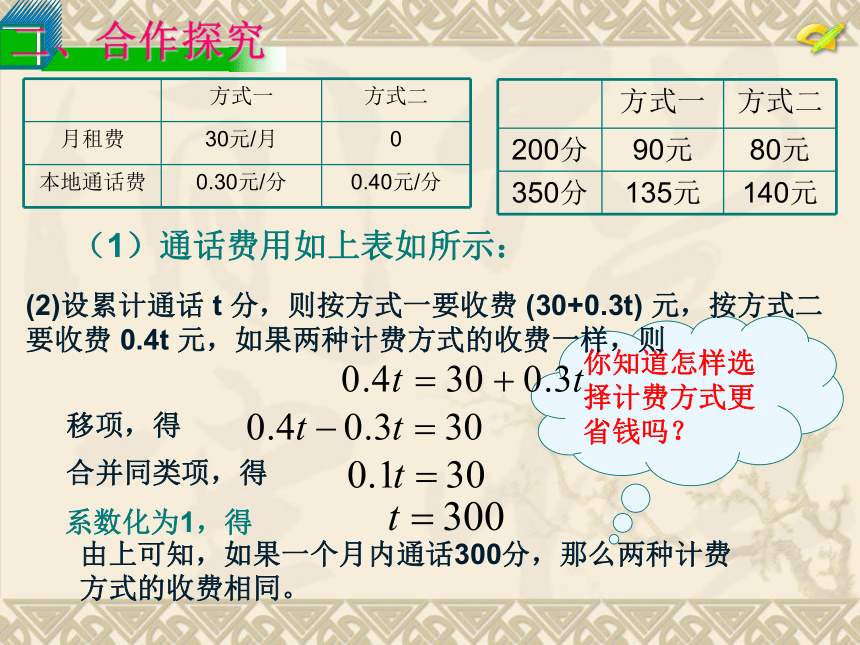
考虑下列问题。(1)一个月内在本地通话200分和350分,按方式一
需交费多少元?按方式二呢?(2)对于某个本地通话时间,会出现两种计费方式
收费一样多吗?你知道怎样选择计费方式更省钱吗?(2)设累计通话 t 分,则按方式一要收费 (30+0.3t) 元,按方式二
要收费 0.4t 元,如果两种计费方式的收费一样,则移项,得合并同类项,得系数化为1,得由上可知,如果一个月内通话300分,那么两种计费
方式的收费相同。(1)通话费用如上表如所示: 【例1】 张师傅加工一批零件,第一天完成的个数与零件的总个数之比是2:5,如果再加工15个,就可以完成这批零件的一半,这批零件共有多少个?解题思路:根据第一天完成个数与零件总个数之比为2:5,可设第一天完成 个零件,零件总数为 个,这批零件的一半为 个,可列方程求解.解:设第一天完成零件的个数为2x个,则零件总个数为5x个,根据题意,得
移项,得 合并同类项,得
系数化为1,得 x=30 所以, 5x=150.
答:这批零件共有150个. 【例2】 三角形三边之比为7:5:4,若中等长度的一边长的2倍比其他两边的和少3 ㎝ ,求三角形的周长?解:设三角形的三边分别为7x ㎝ 、 5x ㎝ 、4x ㎝ ,根据题意,得
2 × 5x=7x+ 4x -3
移项,得 10x-7x- 4x =-3
合并同类项,得 -x=-3
系数化为1,得 x=3
所以,周长为: 7x+5x+ 4x =16x=16 ×3=48( ㎝)
答:三角形的周长为48 ㎝. 【例3】 A、B两地相距450千米,甲、乙两车分别从A、B两地同时出发,相向而行.已知甲车速度为120千米/时,乙车速度为80千米/时,求经过几小时两车相距50千米?解题思路:此题应分相遇前两车相距50千米和相遇后两车相距50千米两种情况讨论作答.解:设经过t小时后两车相距50千米
(1)当甲、乙两车未相遇时,根据题意,得
120t+80t=450-50
解得t=2
(2)当两车相遇后,两车又相距50千米时,根据题意,得
120t+80t=450+50
解得t=2.5
答:经过2小时或2.5小时后,两车相距50千米. 题目中含有比的应用题在设未知数时,一般根据比去设,如果题目告诉的比是a:b,一般设为ax和bx两部分,如果比是a:b:c,一般设为ax,bx,cx,然后找出题目中的等量关系列出方程,并解答.4、关于 的方程 与 的解相同,则a的值为 .5、小明、小华、小丽三个小朋友用积木搭长城,三人用的积木数量之比为1:3:2,数了数,小华用的积木比小丽用的多11块,请你帮小朋友算算共有多少块积木?6、根据下列条件列方程,并求出方程的解
(1)某数的三分之一比它本身小6,求这个数;
(2)一个数的2倍与3的和等于这个数与7的差,求这个数.7、某中学组织七年级的同学去游玩,原计划租用45座客车若干辆,但有15人没有座位,如果租用同样数量的60座客车,则多出一辆且其余客车恰好座满,试问七年级有多少人?原计划租用45座客车多少辆?8、一个两位数的个位数字与十位数字之和为4,如果将个位数字与十位数字对调,所得新数比原数大18,求原两位数是多少?再见
第三章一元一次方程3.2合并同类项与移项(第4课时)朱河镇初级中学七年级数学组本课内容掌握题目中含有比的应用题设未知数的方法建立方程解决实际问题 解下列方程 1、某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200t;如用新工艺,则废水排量比环保限制的最大值少100t.新旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少?思考下列问题:
(1)如果设新工艺废水排量是x吨,则旧工艺废水排量是 吨;
(2)如果设旧工艺废水排量是x吨,则新工艺废水排量是 吨;
(3)由新旧工艺的废水排量比是2:5,我们能否设新、旧工艺的废水排量是2x吨和3x吨?
(4)比较上述几种设未知数的方法,你觉得哪种方法更简单?
(5)题目中的等量关系是根据什么来确定的?环保限制的最大量如何表示?能(3)根据环保限制的最大量的不同表示关系列方程解:设新、旧工艺的废水排量分别为2x吨和3x吨,根据题意,得
5x-200=2x+100
移项,得 5x-2x=100+200
合并同类项,得 3x=300
系数化为1,得 x=100
所以, 2x=200, 5x=500
答:新、旧工艺产生的废水排量分别是200t和500t.2、根据下面的两种移动电话计费方式表,
考虑下列问题。(1)一个月内在本地通话200分和350分,按方式一
需交费多少元?按方式二呢?(2)对于某个本地通话时间,会出现两种计费方式
收费一样多吗?你知道怎样选择计费方式更省钱吗?(2)设累计通话 t 分,则按方式一要收费 (30+0.3t) 元,按方式二
要收费 0.4t 元,如果两种计费方式的收费一样,则移项,得合并同类项,得系数化为1,得由上可知,如果一个月内通话300分,那么两种计费
方式的收费相同。(1)通话费用如上表如所示: 【例1】 张师傅加工一批零件,第一天完成的个数与零件的总个数之比是2:5,如果再加工15个,就可以完成这批零件的一半,这批零件共有多少个?解题思路:根据第一天完成个数与零件总个数之比为2:5,可设第一天完成 个零件,零件总数为 个,这批零件的一半为 个,可列方程求解.解:设第一天完成零件的个数为2x个,则零件总个数为5x个,根据题意,得
移项,得 合并同类项,得
系数化为1,得 x=30 所以, 5x=150.
答:这批零件共有150个. 【例2】 三角形三边之比为7:5:4,若中等长度的一边长的2倍比其他两边的和少3 ㎝ ,求三角形的周长?解:设三角形的三边分别为7x ㎝ 、 5x ㎝ 、4x ㎝ ,根据题意,得
2 × 5x=7x+ 4x -3
移项,得 10x-7x- 4x =-3
合并同类项,得 -x=-3
系数化为1,得 x=3
所以,周长为: 7x+5x+ 4x =16x=16 ×3=48( ㎝)
答:三角形的周长为48 ㎝. 【例3】 A、B两地相距450千米,甲、乙两车分别从A、B两地同时出发,相向而行.已知甲车速度为120千米/时,乙车速度为80千米/时,求经过几小时两车相距50千米?解题思路:此题应分相遇前两车相距50千米和相遇后两车相距50千米两种情况讨论作答.解:设经过t小时后两车相距50千米
(1)当甲、乙两车未相遇时,根据题意,得
120t+80t=450-50
解得t=2
(2)当两车相遇后,两车又相距50千米时,根据题意,得
120t+80t=450+50
解得t=2.5
答:经过2小时或2.5小时后,两车相距50千米. 题目中含有比的应用题在设未知数时,一般根据比去设,如果题目告诉的比是a:b,一般设为ax和bx两部分,如果比是a:b:c,一般设为ax,bx,cx,然后找出题目中的等量关系列出方程,并解答.4、关于 的方程 与 的解相同,则a的值为 .5、小明、小华、小丽三个小朋友用积木搭长城,三人用的积木数量之比为1:3:2,数了数,小华用的积木比小丽用的多11块,请你帮小朋友算算共有多少块积木?6、根据下列条件列方程,并求出方程的解
(1)某数的三分之一比它本身小6,求这个数;
(2)一个数的2倍与3的和等于这个数与7的差,求这个数.7、某中学组织七年级的同学去游玩,原计划租用45座客车若干辆,但有15人没有座位,如果租用同样数量的60座客车,则多出一辆且其余客车恰好座满,试问七年级有多少人?原计划租用45座客车多少辆?8、一个两位数的个位数字与十位数字之和为4,如果将个位数字与十位数字对调,所得新数比原数大18,求原两位数是多少?再见
