【新课标】4.1.2成比例线段 课件(共19张PPT)
文档属性
| 名称 | 【新课标】4.1.2成比例线段 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-24 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
4.1.2成比例线段
北师大版九年级上册
教学目标
1.理解并掌握比例的性质及比例式与等积式的互化.
2.利用比例的性质进行计算.
情景导入
1.线段的比:即两条线段的长度比;
2.成比例线段:四条线段a、b、c、d,如果
(或a∶b=c∶d),那么这四条线段a、b、c、d叫做成比例线段;
如果,那么ad=bc.
如果ad=bc(a、b、c、d都不等于0),那么
新知讲解
B
A
C
D
E
H
F
G
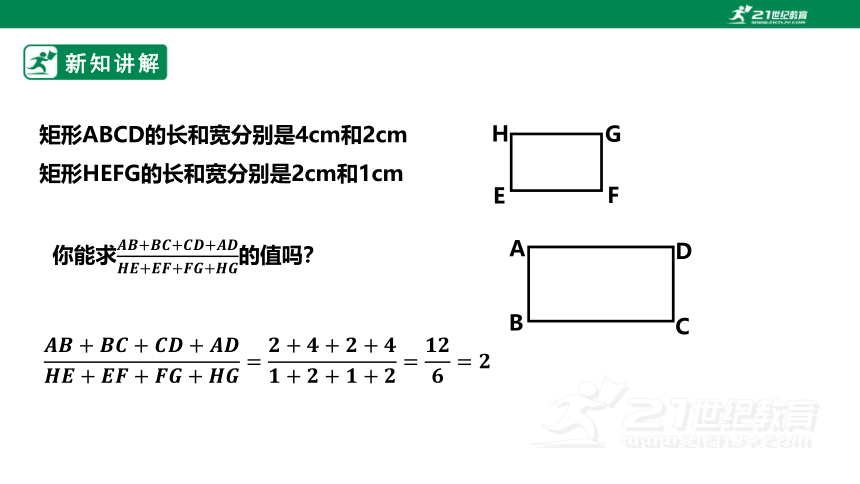
矩形ABCD的长和宽分别是4cm和2cm
矩形HEFG的长和宽分别是2cm和1cm
你能求的值吗?
新知讲解
已知a,b,c,d,e,f 六个数。
如果那么成立吗?为什么?
解:若成立,则有ab+bc+be=ab+ad+af
bc+be=ad+af
∵
∴ad=bc,af=be
∴bc+be=ad+af
∴成立
新知讲解
合比性质:如果,那么
∵ ,在两边同时加上1得,+1 = +1.
∴两边分别通分得:
思考:请仿照上面的方法,证明“如果,则 ”
分比性质
新知讲解
等比性质:如果 (b+d+...+n≠0),那么.
思考:等比性质中,为什么要b+d+...+n≠0这个条件?
因为分母不能为0.
归纳总结
比例的基本性质
典例精析
例2、在△ABC 与△DEF 中,已知 ,且△ABC 的周长为18 cm,求△DEF 的周长.
解:∵∴
∴4(AB+BC+CA)=3(DE+EF+FD)
即(DE+EF+FD)=
又∵△ABC的周长为18 cm,即AB+BC+CA=18 cm,
∴DE+EF+FD = AB + BC + CA)= ×18 = 24(cm), 即△DEF的周长为 24cm.
练一练
已知x∶y∶z=3∶5∶7,求的值.
解:由题意,设x=3k,y=5k,z=7k(k≠0)
则
课堂练习
1.若,则的值为( )
1 B. C. D.
2.已知,则下列等式成立的是( )
B. C. D.y+z=3x
D
D
课堂练习
3.若,则 .
4.若,则 .
课堂练习
5.已知k=,求k的值。
解:当a+b+c=0时,a+b=-c
∴
当a+b+c≠0时,根据等比性质
∴k==2
∴k=-1或k=2
课堂练习
6.已知a,b,c是△ABC的三边长,且≠0.
求:(1) 的值;
(2)若△ABC的周长为90,求各边的长.
解:(1)设=k(k≠0),则a=5k,b=4k,c=6k
∴
(2)由5k+4k+6k=90,解得k=6
∴a=5×6=30,b=4×6=24,c=6×6=36
课堂总结
比例的合比性质
如果,那么.
比例的等比性质
如果
那么.
板书设计
课题:4.1.2成比例线段
1.合比性质
2.等比性质
作业布置
教材第81页习题4.2第1、2、3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
4.1.2成比例线段
北师大版九年级上册
教学目标
1.理解并掌握比例的性质及比例式与等积式的互化.
2.利用比例的性质进行计算.
情景导入
1.线段的比:即两条线段的长度比;
2.成比例线段:四条线段a、b、c、d,如果
(或a∶b=c∶d),那么这四条线段a、b、c、d叫做成比例线段;
如果,那么ad=bc.
如果ad=bc(a、b、c、d都不等于0),那么
新知讲解
B
A
C
D
E
H
F
G
矩形ABCD的长和宽分别是4cm和2cm
矩形HEFG的长和宽分别是2cm和1cm
你能求的值吗?
新知讲解
已知a,b,c,d,e,f 六个数。
如果那么成立吗?为什么?
解:若成立,则有ab+bc+be=ab+ad+af
bc+be=ad+af
∵
∴ad=bc,af=be
∴bc+be=ad+af
∴成立
新知讲解
合比性质:如果,那么
∵ ,在两边同时加上1得,+1 = +1.
∴两边分别通分得:
思考:请仿照上面的方法,证明“如果,则 ”
分比性质
新知讲解
等比性质:如果 (b+d+...+n≠0),那么.
思考:等比性质中,为什么要b+d+...+n≠0这个条件?
因为分母不能为0.
归纳总结
比例的基本性质
典例精析
例2、在△ABC 与△DEF 中,已知 ,且△ABC 的周长为18 cm,求△DEF 的周长.
解:∵∴
∴4(AB+BC+CA)=3(DE+EF+FD)
即(DE+EF+FD)=
又∵△ABC的周长为18 cm,即AB+BC+CA=18 cm,
∴DE+EF+FD = AB + BC + CA)= ×18 = 24(cm), 即△DEF的周长为 24cm.
练一练
已知x∶y∶z=3∶5∶7,求的值.
解:由题意,设x=3k,y=5k,z=7k(k≠0)
则
课堂练习
1.若,则的值为( )
1 B. C. D.
2.已知,则下列等式成立的是( )
B. C. D.y+z=3x
D
D
课堂练习
3.若,则 .
4.若,则 .
课堂练习
5.已知k=,求k的值。
解:当a+b+c=0时,a+b=-c
∴
当a+b+c≠0时,根据等比性质
∴k==2
∴k=-1或k=2
课堂练习
6.已知a,b,c是△ABC的三边长,且≠0.
求:(1) 的值;
(2)若△ABC的周长为90,求各边的长.
解:(1)设=k(k≠0),则a=5k,b=4k,c=6k
∴
(2)由5k+4k+6k=90,解得k=6
∴a=5×6=30,b=4×6=24,c=6×6=36
课堂总结
比例的合比性质
如果,那么.
比例的等比性质
如果
那么.
板书设计
课题:4.1.2成比例线段
1.合比性质
2.等比性质
作业布置
教材第81页习题4.2第1、2、3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
