人教版数学九年级上册 24.1.3弧、弦、圆心角 课件(共21张PPT)
文档属性
| 名称 | 人教版数学九年级上册 24.1.3弧、弦、圆心角 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-24 16:04:17 | ||
图片预览







文档简介
(共21张PPT)
第二十四章 圆
24.1.3 弧、弦、圆心角
欣赏动画:折扇的收拢和展开.
圆是中心对称图形,
圆心是它的对称中心.
把圆绕圆心旋转任意
一个角度,所得的图形
与原图形重合,即圆有
旋转不变性.
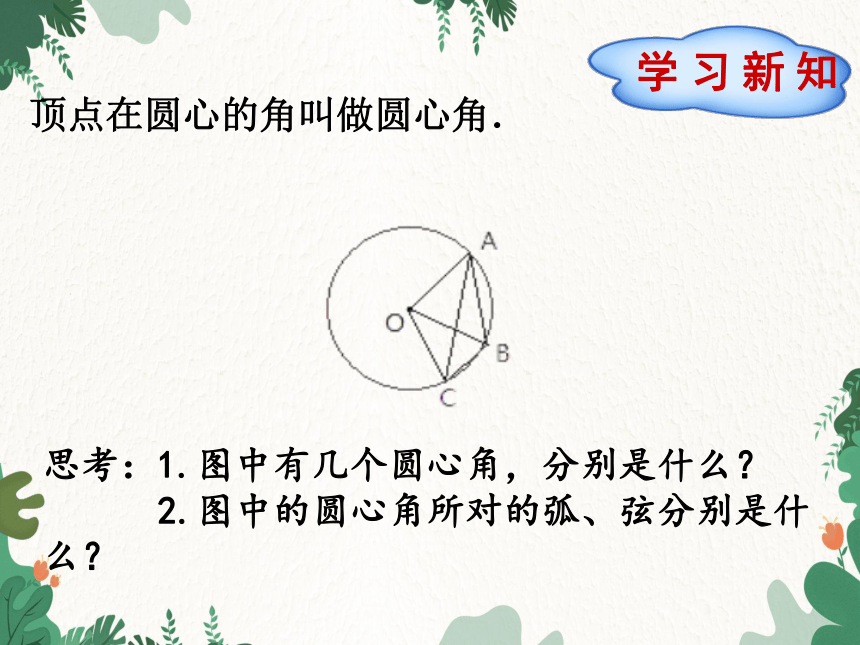
顶点在圆心的角叫做圆心角.
学 习 新 知
思考:1.图中有几个圆心角,分别是什么?
2.图中的圆心角所对的弧、弦分别是什么?
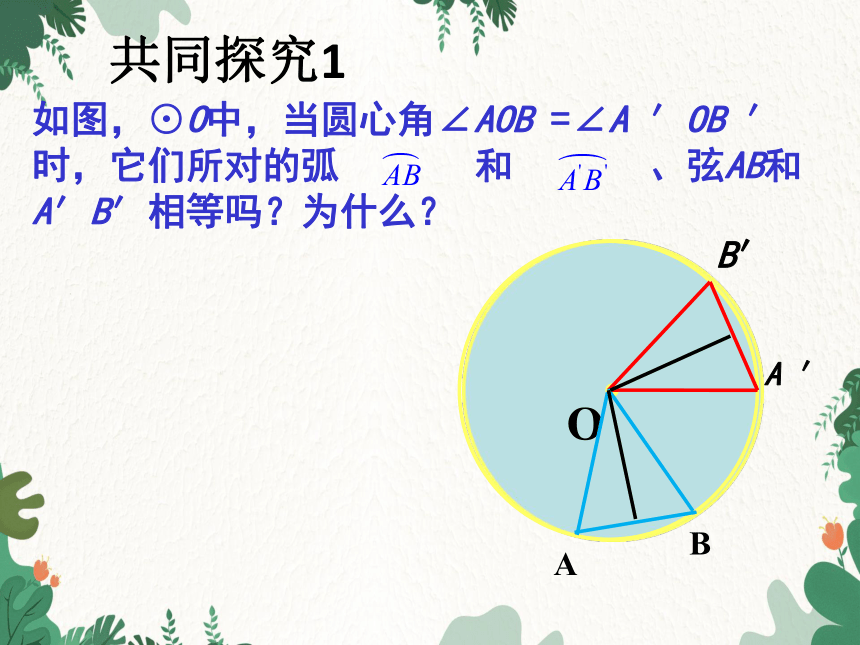
共同探究1
如图,⊙O中,当圆心角∠AOB =∠A ′OB ′ 时,它们所对的弧 和 、弦AB和A′B′相等吗?为什么?
O
A
B
A ′
B′
1.将∠AOB旋转到∠A ′ OB ′的位置,它能否与∠AOB完全重合?
2.如果能重合,你会发现哪些等量关系?
3.你能证明这些结论吗?
4.如果圆心角∠AOB= ∠A ′ OB ′ ,你能否得到相同的结论?
5.你能用语言叙述上面的命题吗?
思考
将∠AOB连同 绕圆心O旋转,使射线OA与OA′重合.
∵∠AOB=∠A′OB′,∴射线OB与OB′重合.
又OA=OA′,OB=OB′,
∴点A与A′重合,点B与B′重合,
因此, 与 重合,AB与A′B′重合.即
= 、AB=A′B′.
分析:
定理:在同圆或等圆中,相等的圆心
角所对的弧相等,所对的弦也相等.
共同探究2
思考:
1.在圆心角性质定理中,为什么要说“在同圆或等圆中”?能不能去掉?
2.在同圆或等圆中,如果两条弧相等,能得到什么结论?
3.在同圆或等圆中,如果两条弦相等,能得到什么结论?
1.圆上各点到定点(圆心O)的距离都等于定长(半径r);
2.到定点的距离等于定长的点都在同一个圆上.
圆的第二定义:圆心为O,半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧相等.
即:在同圆或等圆中,两个圆心角、两条弧、两条弦、两条弦心距中有一组量相等,它们所对应的其余各组量也相等.
·
A
B
C
D
O
填空:如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么 , .
(2)如果 ,那么 , .
(3)如果∠AOB=∠COD,那么 , .
例3
如图,在⊙O中, ,∠ACB=60°.
求证:∠AOB=∠BOC=∠AOC.
A
B
C
O
要证圆心角∠AOB=∠BOC=∠AOC,需证 或 ;
而 ,可得 ,又∠ACB=60°,所以△ABC是
三角形,则 ,从而得证.
1.圆是中心对称图形,圆有旋转不变性.
2.圆心角概念:顶点在圆心的角.
3.圆心角、弧、弦之间的关系:在同圆或等圆中,两个圆心角、两条弧、两条弦、两条弦心距中有一组量相等,它们所对应的其余各组量也相等.
4.利用同圆或等圆中圆心角、弦、弧之间的关系可以证明角、弦或弧相等.
检测反馈
1.在同圆或等圆中,如果 ,那么AB与CD的关系是( )
AB>CD B. AB=CD
C. AB<CD D.无法确定
解析:在同圆或等圆中,相等的弧所对的弦相等,所以由 得AB=CD,故选B.
B
C
2.如图,已知AB是⊙O的直径,点C、D是 上的三等分点,∠AOE=600,则∠COE=( )
A. 40O B.60O C.80O D.120O
解析:∵∠AOE=60°,
∴∠BOE=180°-∠AOE=120°,∴ 的度数是120°,∵C、D是 上的三等分点,∴弧CD与弧ED的度数都是40°,∴∠COE=80°.故选C.
A
B
C
D
E
O
3.如图,在⊙O中, ,∠A=400,则∠B= .
解析:∵ ,∴AB=AC,∵∠A=40°,∴∠B=∠C=(180°-∠A)÷2=70°.
故填70°.
70°
4.如图,在⊙O中,AB、CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为EF.
(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
(2)如果OE=OF,那么 与 的大小有什么关系?AB与CD的大小有什么关系?为什么?∠AOB与∠COD呢?
解:
(1)OE=OF,
理由是:∵OE⊥AB, OF⊥CD,
OA=OB, OC=OD
∴∠OEB=∠OFD=90°,∠EOB= ∠AOB,
∠FOD= ∠COD,
∵∠AOB=∠COD,∴∠EOB=∠FOD,
又∵OB=OD,∴△EOB≌△FOD(AAS),
∴OE=OF.
(2) ,AB=CD ,∠AOB=∠COD, 理由是:
∵OE⊥AB,OF⊥CD,∴∠OEB=∠OFD=90°
∴Rt△BEO≌Rt△DFO(HL),∴BE=DF,
∵OB=OD,OE=OF,
由垂径定理得AB=2BE,CD=2DF,
∴AB=CD, ∴ ,∠AOB=∠COD.
第二十四章 圆
24.1.3 弧、弦、圆心角
欣赏动画:折扇的收拢和展开.
圆是中心对称图形,
圆心是它的对称中心.
把圆绕圆心旋转任意
一个角度,所得的图形
与原图形重合,即圆有
旋转不变性.
顶点在圆心的角叫做圆心角.
学 习 新 知
思考:1.图中有几个圆心角,分别是什么?
2.图中的圆心角所对的弧、弦分别是什么?
共同探究1
如图,⊙O中,当圆心角∠AOB =∠A ′OB ′ 时,它们所对的弧 和 、弦AB和A′B′相等吗?为什么?
O
A
B
A ′
B′
1.将∠AOB旋转到∠A ′ OB ′的位置,它能否与∠AOB完全重合?
2.如果能重合,你会发现哪些等量关系?
3.你能证明这些结论吗?
4.如果圆心角∠AOB= ∠A ′ OB ′ ,你能否得到相同的结论?
5.你能用语言叙述上面的命题吗?
思考
将∠AOB连同 绕圆心O旋转,使射线OA与OA′重合.
∵∠AOB=∠A′OB′,∴射线OB与OB′重合.
又OA=OA′,OB=OB′,
∴点A与A′重合,点B与B′重合,
因此, 与 重合,AB与A′B′重合.即
= 、AB=A′B′.
分析:
定理:在同圆或等圆中,相等的圆心
角所对的弧相等,所对的弦也相等.
共同探究2
思考:
1.在圆心角性质定理中,为什么要说“在同圆或等圆中”?能不能去掉?
2.在同圆或等圆中,如果两条弧相等,能得到什么结论?
3.在同圆或等圆中,如果两条弦相等,能得到什么结论?
1.圆上各点到定点(圆心O)的距离都等于定长(半径r);
2.到定点的距离等于定长的点都在同一个圆上.
圆的第二定义:圆心为O,半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧相等.
即:在同圆或等圆中,两个圆心角、两条弧、两条弦、两条弦心距中有一组量相等,它们所对应的其余各组量也相等.
·
A
B
C
D
O
填空:如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么 , .
(2)如果 ,那么 , .
(3)如果∠AOB=∠COD,那么 , .
例3
如图,在⊙O中, ,∠ACB=60°.
求证:∠AOB=∠BOC=∠AOC.
A
B
C
O
要证圆心角∠AOB=∠BOC=∠AOC,需证 或 ;
而 ,可得 ,又∠ACB=60°,所以△ABC是
三角形,则 ,从而得证.
1.圆是中心对称图形,圆有旋转不变性.
2.圆心角概念:顶点在圆心的角.
3.圆心角、弧、弦之间的关系:在同圆或等圆中,两个圆心角、两条弧、两条弦、两条弦心距中有一组量相等,它们所对应的其余各组量也相等.
4.利用同圆或等圆中圆心角、弦、弧之间的关系可以证明角、弦或弧相等.
检测反馈
1.在同圆或等圆中,如果 ,那么AB与CD的关系是( )
AB>CD B. AB=CD
C. AB<CD D.无法确定
解析:在同圆或等圆中,相等的弧所对的弦相等,所以由 得AB=CD,故选B.
B
C
2.如图,已知AB是⊙O的直径,点C、D是 上的三等分点,∠AOE=600,则∠COE=( )
A. 40O B.60O C.80O D.120O
解析:∵∠AOE=60°,
∴∠BOE=180°-∠AOE=120°,∴ 的度数是120°,∵C、D是 上的三等分点,∴弧CD与弧ED的度数都是40°,∴∠COE=80°.故选C.
A
B
C
D
E
O
3.如图,在⊙O中, ,∠A=400,则∠B= .
解析:∵ ,∴AB=AC,∵∠A=40°,∴∠B=∠C=(180°-∠A)÷2=70°.
故填70°.
70°
4.如图,在⊙O中,AB、CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为EF.
(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
(2)如果OE=OF,那么 与 的大小有什么关系?AB与CD的大小有什么关系?为什么?∠AOB与∠COD呢?
解:
(1)OE=OF,
理由是:∵OE⊥AB, OF⊥CD,
OA=OB, OC=OD
∴∠OEB=∠OFD=90°,∠EOB= ∠AOB,
∠FOD= ∠COD,
∵∠AOB=∠COD,∴∠EOB=∠FOD,
又∵OB=OD,∴△EOB≌△FOD(AAS),
∴OE=OF.
(2) ,AB=CD ,∠AOB=∠COD, 理由是:
∵OE⊥AB,OF⊥CD,∴∠OEB=∠OFD=90°
∴Rt△BEO≌Rt△DFO(HL),∴BE=DF,
∵OB=OD,OE=OF,
由垂径定理得AB=2BE,CD=2DF,
∴AB=CD, ∴ ,∠AOB=∠COD.
同课章节目录
