人教版数学八年级上册 第十一章 三角形小专题(3) 三角形中角度计算的常见类型 课件 (共13张PPT)
文档属性
| 名称 | 人教版数学八年级上册 第十一章 三角形小专题(3) 三角形中角度计算的常见类型 课件 (共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-24 18:36:05 | ||
图片预览


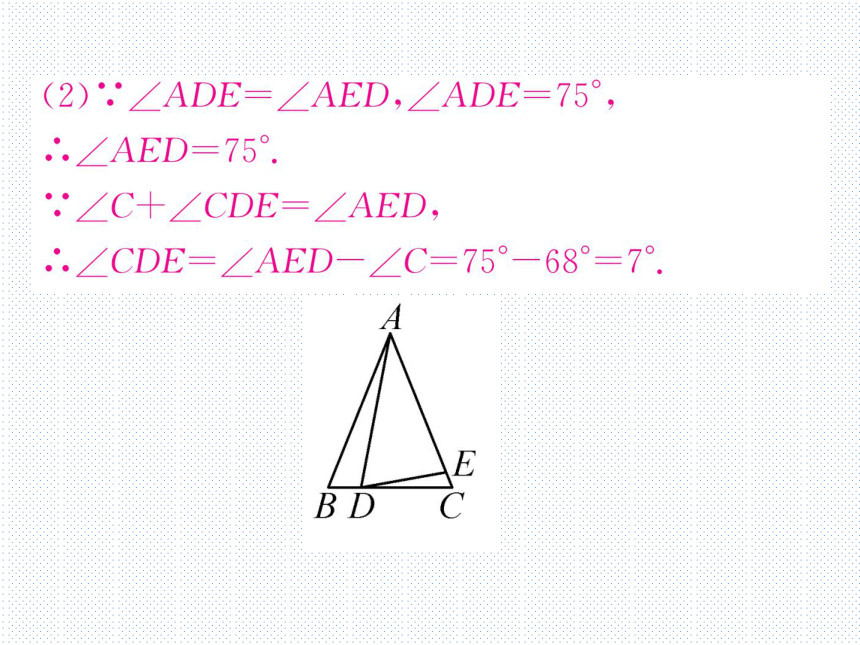
文档简介
(共13张PPT)
类型①直接利用三角形的内、外角性质求
角度
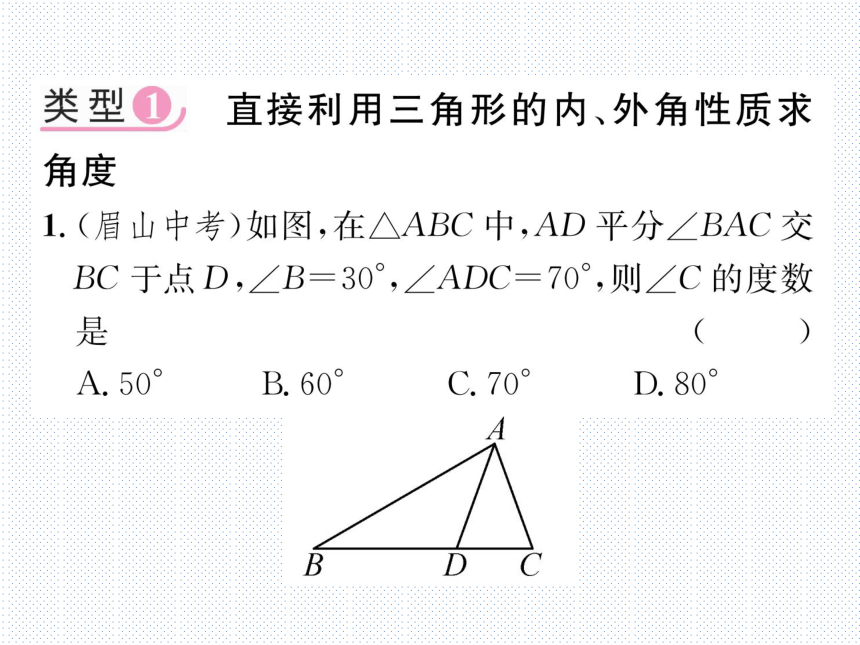
1.(眉山中考)如图,在△ABC中,AD平分∠BAC交
BC于点D,∠B=30°,∠ADC=70°,则∠C的度数
是
(C)
A.50°
B.60°
C.70°
D.80°
B
D
(第1题图)
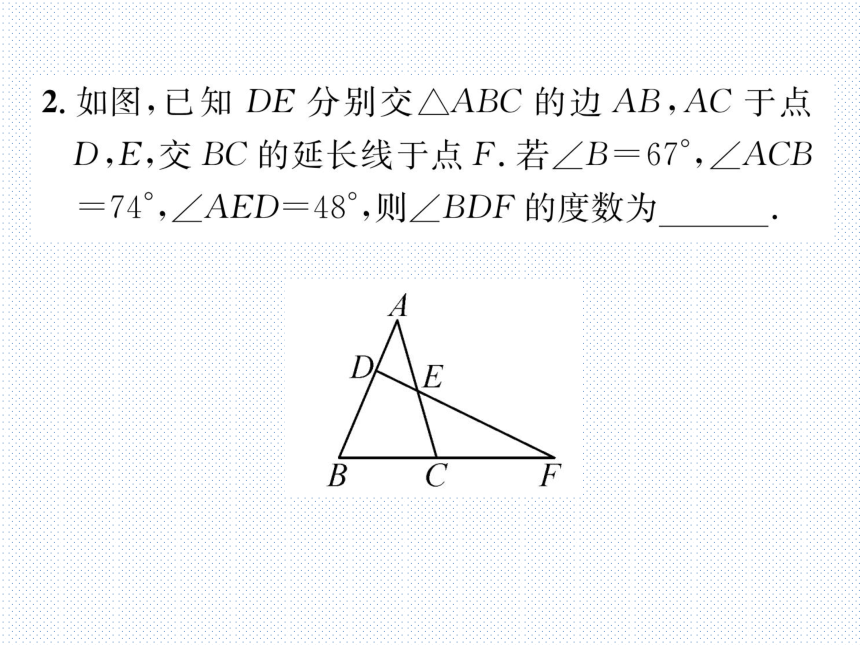
(第2题图)
2.如图,已知DE分别交△ABC的边AB,AC于点
D,E,交BC的延长线于点F.若∠B=67°,∠ACB
=74°,∠AED=48°,则∠BDF的度数为87°.
3.如图,已知在△ABC中,∠B=∠C,D为边BC上
一点(不与点B,C重合),点E为边AC上一点,
∠ADE=∠AED,∠BAC=44°.
(1)求∠C的度数;
(2)若∠ADE=75°,求∠CDE的度数.
解:(1).∠BAC=44°,
.∠B+∠C=180°-∠BAC=180°-44°
=136°.
∠B=∠C,.2∠C=136°,
.∠C=68°;
(2).∠ADE=∠AED,∠ADE=75°,
∴.∠AED=75
'∠C+∠CDE=∠AED,
.∴.∠CDE=∠AED-∠C=75°-68°=7°
类型②借助三角形的角平分线、高的性质
求角度
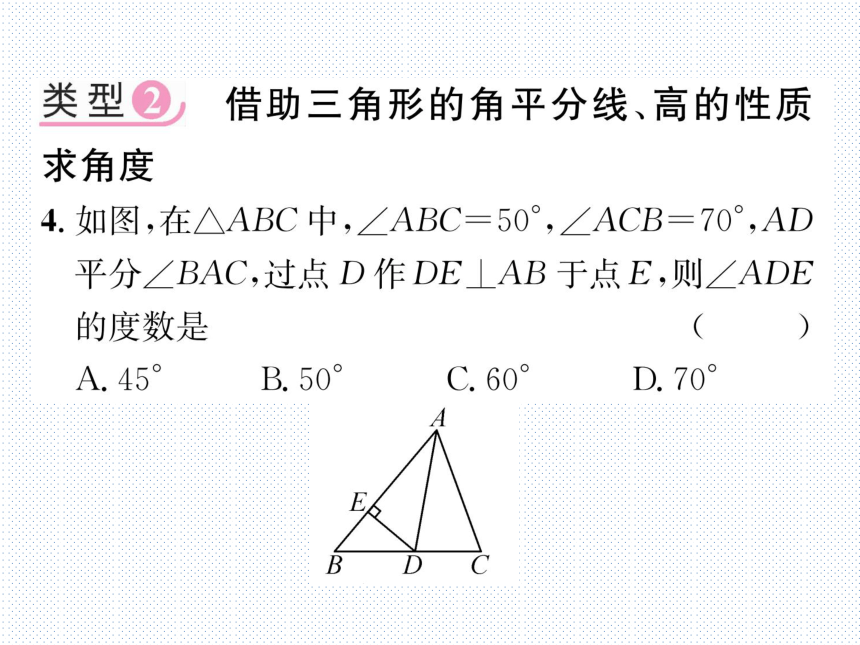
4.如图,在△ABC中,∠ABC=50°,∠ACB=70°,AD
平分∠BAC,过点D作DE⊥AB于点E,则∠ADE
的度数是
(C)
A.45°
B.50°
C.60°
D.70°
B
D
D
(第4题图)
(第5题图)
5.如图,在△ABC中,∠ABC,∠ACB的平分线相交
于点O,OD⊥OC交BC于点D.若∠A=80°,则
∠BOD=40°·
类型③
借助平行线的性质求角度
6.如图,a∥b,∠1+∠2=75°,则∠3十∠4=105°
4
B
万
(第6题图)
(第7题图)
7.如图,CE平分∠ACD,F为CA延长线上一点,FG∥
CE交AB于点G,∠ACD=100°,∠AGF=20°,则
∠BAC的度数为70°,∠B的度数为30°
类型④借助三角板的角度特征求角度
8.如图,直线AB∥CD,一个含60°角的直角三角板
EFG(∠E=60°)的直角顶点F在直线AB上,斜边
EG与AB相交于点H,CD与FG相交于点M.若
∠AHG=50°,则∠FMD等于
(B)
A.10°
B.209
C.30°
D.50
H
B
M
G
B
(第8题图)
(第9题图)
9.(鄂州中考)一副学生用的三角板如图放置,则
∠AOD的度数为105°
类型⑤借助折叠的性质求角度
10.如图,在Rt△ABC中,∠ACB=90°,
E
∠A=48°,将其折叠,E是点A落在
边BC上的点,折痕为CD,则∠EDB
的度数为6°.
11.如图,在△ABC中,点D是BC边上的一点,∠B
50°,∠BAD=30°,将△ABD沿AD折叠得到
△AED,AE与BC相交于点F.
(1)∠AFC=
(2)求∠EDF的度数.
解:(1)110°;
(2).∠B=50°,
/BAD=30°,
.∴.∠ADB=180°-50°-30
=100°,
∴.∠ADF=180°-∠ADB=80°.
.'△ABD沿AD折叠得到△AED,
.∠ADE=∠ADB=100°,
∴.∠EDF=∠ADE-∠ADF=100°-80°=20°.
类型①直接利用三角形的内、外角性质求
角度
1.(眉山中考)如图,在△ABC中,AD平分∠BAC交
BC于点D,∠B=30°,∠ADC=70°,则∠C的度数
是
(C)
A.50°
B.60°
C.70°
D.80°
B
D
(第1题图)
(第2题图)
2.如图,已知DE分别交△ABC的边AB,AC于点
D,E,交BC的延长线于点F.若∠B=67°,∠ACB
=74°,∠AED=48°,则∠BDF的度数为87°.
3.如图,已知在△ABC中,∠B=∠C,D为边BC上
一点(不与点B,C重合),点E为边AC上一点,
∠ADE=∠AED,∠BAC=44°.
(1)求∠C的度数;
(2)若∠ADE=75°,求∠CDE的度数.
解:(1).∠BAC=44°,
.∠B+∠C=180°-∠BAC=180°-44°
=136°.
∠B=∠C,.2∠C=136°,
.∠C=68°;
(2).∠ADE=∠AED,∠ADE=75°,
∴.∠AED=75
'∠C+∠CDE=∠AED,
.∴.∠CDE=∠AED-∠C=75°-68°=7°
类型②借助三角形的角平分线、高的性质
求角度
4.如图,在△ABC中,∠ABC=50°,∠ACB=70°,AD
平分∠BAC,过点D作DE⊥AB于点E,则∠ADE
的度数是
(C)
A.45°
B.50°
C.60°
D.70°
B
D
D
(第4题图)
(第5题图)
5.如图,在△ABC中,∠ABC,∠ACB的平分线相交
于点O,OD⊥OC交BC于点D.若∠A=80°,则
∠BOD=40°·
类型③
借助平行线的性质求角度
6.如图,a∥b,∠1+∠2=75°,则∠3十∠4=105°
4
B
万
(第6题图)
(第7题图)
7.如图,CE平分∠ACD,F为CA延长线上一点,FG∥
CE交AB于点G,∠ACD=100°,∠AGF=20°,则
∠BAC的度数为70°,∠B的度数为30°
类型④借助三角板的角度特征求角度
8.如图,直线AB∥CD,一个含60°角的直角三角板
EFG(∠E=60°)的直角顶点F在直线AB上,斜边
EG与AB相交于点H,CD与FG相交于点M.若
∠AHG=50°,则∠FMD等于
(B)
A.10°
B.209
C.30°
D.50
H
B
M
G
B
(第8题图)
(第9题图)
9.(鄂州中考)一副学生用的三角板如图放置,则
∠AOD的度数为105°
类型⑤借助折叠的性质求角度
10.如图,在Rt△ABC中,∠ACB=90°,
E
∠A=48°,将其折叠,E是点A落在
边BC上的点,折痕为CD,则∠EDB
的度数为6°.
11.如图,在△ABC中,点D是BC边上的一点,∠B
50°,∠BAD=30°,将△ABD沿AD折叠得到
△AED,AE与BC相交于点F.
(1)∠AFC=
(2)求∠EDF的度数.
解:(1)110°;
(2).∠B=50°,
/BAD=30°,
.∴.∠ADB=180°-50°-30
=100°,
∴.∠ADF=180°-∠ADB=80°.
.'△ABD沿AD折叠得到△AED,
.∠ADE=∠ADB=100°,
∴.∠EDF=∠ADE-∠ADF=100°-80°=20°.
