人教版数学八年级上册>第十一章 三角形小专题(1) 探究三角形角平分线相关的结论 课件(共12张PPT)
文档属性
| 名称 | 人教版数学八年级上册>第十一章 三角形小专题(1) 探究三角形角平分线相关的结论 课件(共12张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-24 18:39:13 | ||
图片预览



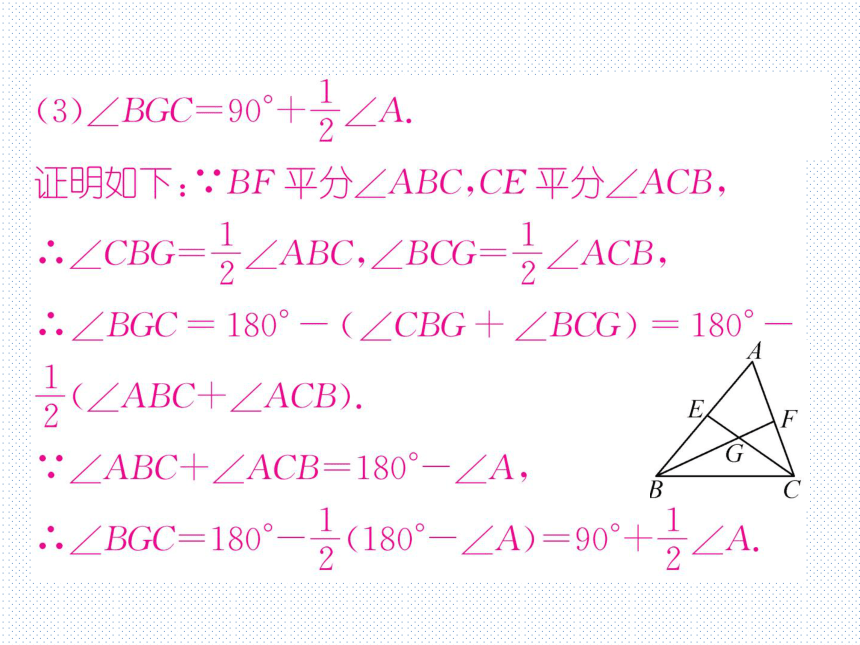

文档简介
(共12张PPT)
《名师测控》
人教版-八年级上册 数学
类型①两内角平分线的夹角
1.如图,△ABC的∠ABC和∠ACB的平分线BF,
CE相交于点G.
(1)若∠ABC=50°,∠ACB=70°,则∠BGC=;
(2)若∠A=50°,则∠BGC=
(3)猜想∠BG℃与∠A之间的数量关系,并加以证明.
解:(1)120°;
(2)115°;
(3)∠BCC=90+2∠A.
证明如下:BF平分∠ABC,CE平分∠ACB,
÷∠CBG-2∠ABC.∠BG-2∠AB.
∴.∠BGC=180°-(∠CBG+∠BCG)=180°
2(∠ABC+∠ACB.
.'∠ABC+∠ACB=180°-∠A,
.∠BGC=180°-2180°-∠A)=90+2∠A.
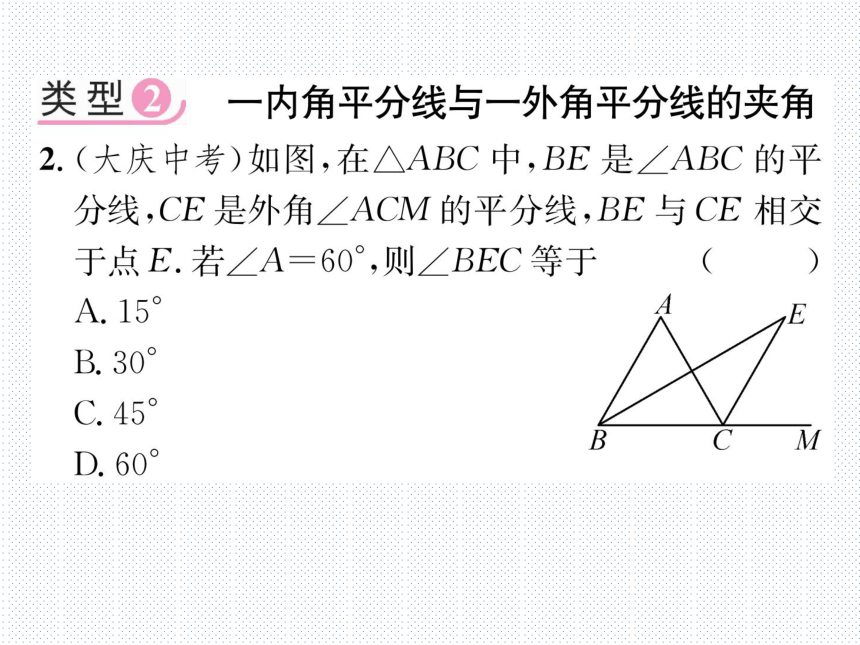
类型②一内角平分线与一外角平分线的夹角
2.(大庆中考)如图,在△ABC中,BE是∠ABC的平
分线,CE是外角∠ACM的平分线,BE与CE相交
于点E.若∠A=60°,则∠BEC等于
(B)
A.15°
B.30°
C.45
D.60°
3.如图,点P是△ABC的内角∠ABC和外角∠ACD
的平分线的交点,试探究∠P与∠A之间的数量
关系.
解:BP平分∠ABC,
÷∠PBC=2∠ABC
.CP平分∠ACD,
∴∠PCD-2∠ACD.
.·∠ACD=∠ABC+∠A,∠PCD=∠PBC+
∠P,
·∠P=∠PCD-∠PBC=(∠ACD-∠ABC
∠A.
=1
4.如图,在△ABC中,外角∠ACD的平分线与∠ABC
的平分线交于点A1,∠ABC的平分线与∠ACD
的平分线交于点A2,则∠A2与∠A有怎样的数量
关系?继续作∠ABC与∠A2CD的平分线可得
∠A3,如此下去可得∠A4,…,∠A,,那么猜想∠A
与∠A又有怎样的数量关系?并求出当∠A=64
时,∠A4的度数
解:“∠A,CD-2∠ABC+
∠A1,
.2∠ACD=∠ABC+B
2∠A1.
又.2∠ACD=∠ACD=∠ABC+∠A,
∴2∠A=∠A,即∠A=号∠A.
同理,得∠A,-2∠A-∠A,∠A.-∠A,
当∠A=640时,∠A=安×64°=4
类型③两外角平分线的夹角
5.如图,在△ABC中,∠A=50°,∠ABC和
∠ACB的外角平分线相交于点D,则
∠BDC=65°
6.如图,点P是△ABC的两个外角∠EBC,
∠FCB的平分线的交点,试探究∠P与∠A之间的
数量关系,
解:.'∠EBC=∠ACB+∠A,
∠FCB=∠ABC+∠A,
∴.∠EBC+∠FCB=∠ACB+∠A
+∠ABC+∠A=180°+∠A.
.'BP,CP分别是∠EBC,∠FCB的平分线,
:∠PBC=2∠EC,∠PCB=2∠FCB,
:∠PBC+∠PCB=(∠EBC+∠FCB)=
2180+∠A)=90+2∠A,
∴.∠P=180°-(∠PBC+∠PCB)=180°-(90°+
2∠A)=90°-2∠A
《名师测控》
人教版-八年级上册 数学
类型①两内角平分线的夹角
1.如图,△ABC的∠ABC和∠ACB的平分线BF,
CE相交于点G.
(1)若∠ABC=50°,∠ACB=70°,则∠BGC=;
(2)若∠A=50°,则∠BGC=
(3)猜想∠BG℃与∠A之间的数量关系,并加以证明.
解:(1)120°;
(2)115°;
(3)∠BCC=90+2∠A.
证明如下:BF平分∠ABC,CE平分∠ACB,
÷∠CBG-2∠ABC.∠BG-2∠AB.
∴.∠BGC=180°-(∠CBG+∠BCG)=180°
2(∠ABC+∠ACB.
.'∠ABC+∠ACB=180°-∠A,
.∠BGC=180°-2180°-∠A)=90+2∠A.
类型②一内角平分线与一外角平分线的夹角
2.(大庆中考)如图,在△ABC中,BE是∠ABC的平
分线,CE是外角∠ACM的平分线,BE与CE相交
于点E.若∠A=60°,则∠BEC等于
(B)
A.15°
B.30°
C.45
D.60°
3.如图,点P是△ABC的内角∠ABC和外角∠ACD
的平分线的交点,试探究∠P与∠A之间的数量
关系.
解:BP平分∠ABC,
÷∠PBC=2∠ABC
.CP平分∠ACD,
∴∠PCD-2∠ACD.
.·∠ACD=∠ABC+∠A,∠PCD=∠PBC+
∠P,
·∠P=∠PCD-∠PBC=(∠ACD-∠ABC
∠A.
=1
4.如图,在△ABC中,外角∠ACD的平分线与∠ABC
的平分线交于点A1,∠ABC的平分线与∠ACD
的平分线交于点A2,则∠A2与∠A有怎样的数量
关系?继续作∠ABC与∠A2CD的平分线可得
∠A3,如此下去可得∠A4,…,∠A,,那么猜想∠A
与∠A又有怎样的数量关系?并求出当∠A=64
时,∠A4的度数
解:“∠A,CD-2∠ABC+
∠A1,
.2∠ACD=∠ABC+B
2∠A1.
又.2∠ACD=∠ACD=∠ABC+∠A,
∴2∠A=∠A,即∠A=号∠A.
同理,得∠A,-2∠A-∠A,∠A.-∠A,
当∠A=640时,∠A=安×64°=4
类型③两外角平分线的夹角
5.如图,在△ABC中,∠A=50°,∠ABC和
∠ACB的外角平分线相交于点D,则
∠BDC=65°
6.如图,点P是△ABC的两个外角∠EBC,
∠FCB的平分线的交点,试探究∠P与∠A之间的
数量关系,
解:.'∠EBC=∠ACB+∠A,
∠FCB=∠ABC+∠A,
∴.∠EBC+∠FCB=∠ACB+∠A
+∠ABC+∠A=180°+∠A.
.'BP,CP分别是∠EBC,∠FCB的平分线,
:∠PBC=2∠EC,∠PCB=2∠FCB,
:∠PBC+∠PCB=(∠EBC+∠FCB)=
2180+∠A)=90+2∠A,
∴.∠P=180°-(∠PBC+∠PCB)=180°-(90°+
2∠A)=90°-2∠A
