人教版数学八年级上册小专题(2) 三角形的重要线段之间的夹角问题课件 (共13张PPT)
文档属性
| 名称 | 人教版数学八年级上册小专题(2) 三角形的重要线段之间的夹角问题课件 (共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-24 18:40:09 | ||
图片预览


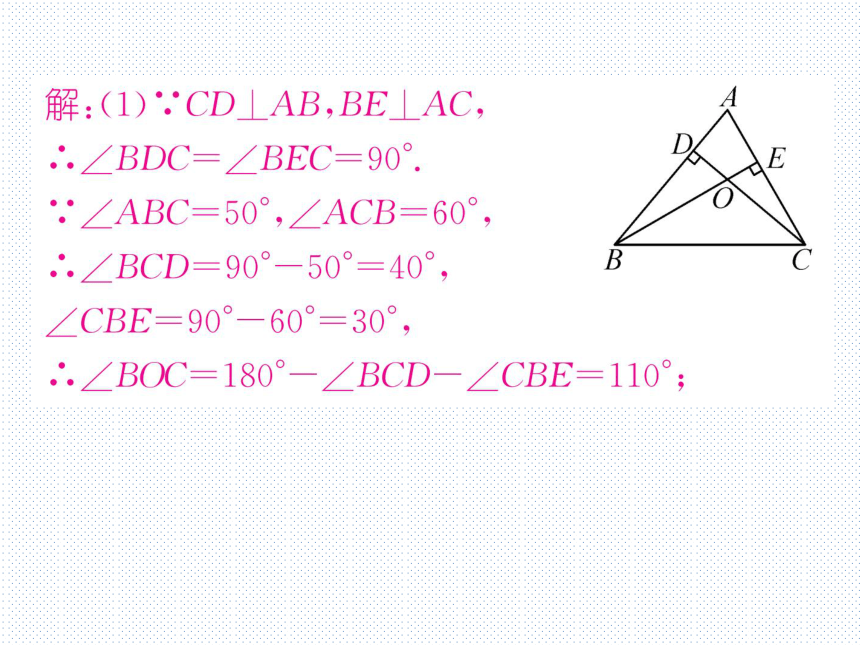
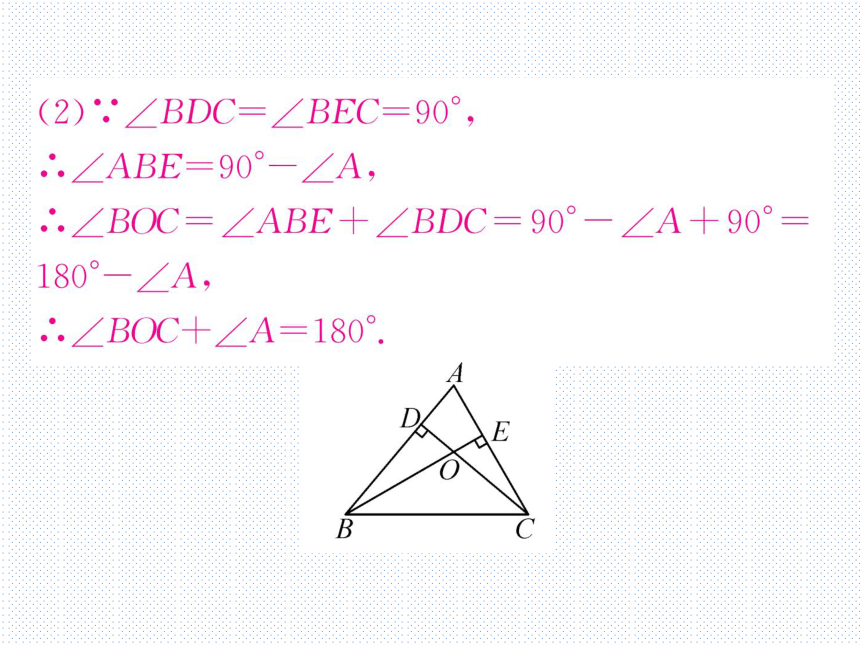

文档简介
(共13张PPT)
类型①三角形中两条高的夹角
1.如图,在△ABC中,CD,BE分别是AB,AC边上的
高,BE,CD相交于点O.
(1)若∠ABC=50°,∠ACB=60°,求∠BO℃的度数;
(2)求证:∠BOC+∠A=180°.
解:(1).CD⊥AB,BE⊥AC,
.∠BDC=∠BEC=90°
.∠ABC=50°,∠ACB=60°,
.∠BCD=90°-50°=40°,
∠CBE=90°-60°=30°,
.∠BOC=180°-∠BCD-∠CBE=110°;
(2).∠BDC=∠BEC=90°,
.∠ABE=90°-∠A,
∴.∠BOC=∠ABE+∠BDC=90°-∠A+90°=
180°-∠A,
.∴.∠BOC+∠A=180°.
类型②三角形同一条边上的高与角平分线
的夹角
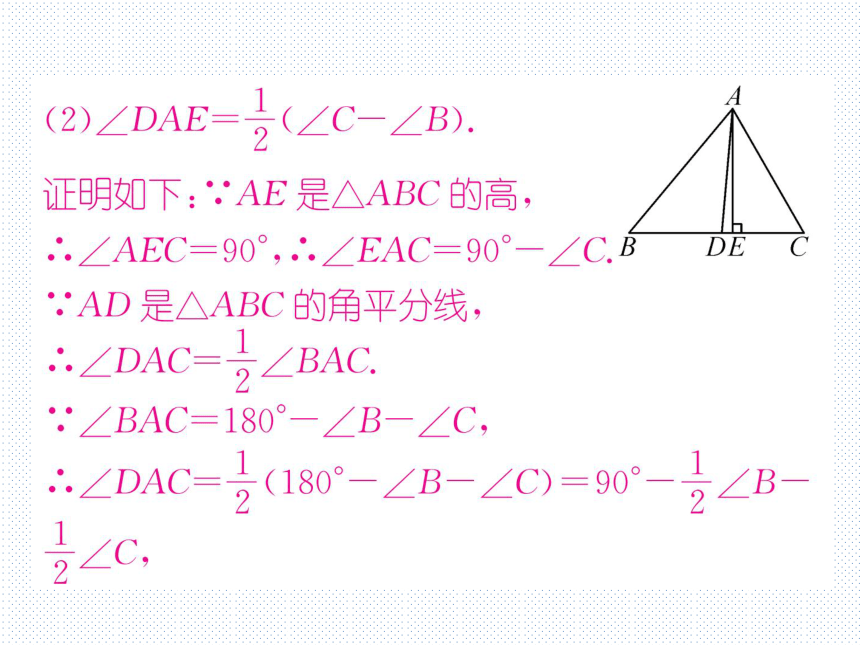
2.如图,AD,AE分别是△ABC的角平分线和高.
(1)若∠B=50°,∠C=60°,则∠DAE=
(2)若∠C>∠B,猜想∠DAE与∠C-∠B之间的
数量关系,并加以证明.
解:(1)5°;
(2)∠DAE=2(∠C-∠B).
证明如下:.'AE是△ABC的高,
DE
∴.∠AEC=90°,.∴.∠EAC=90°-∠C
AD是△ABC的角平分线,
∠DAC=2∠BAC.
.∠BAC=180°-∠B-∠C,
÷∠DAC=2(180°-∠B-∠C)=90-2∠B
∠C,
1
∠B
∴.∠DAE=∠DAC-∠EAC=90°-1
2∠C-(90°-∠C)=2(∠C-∠B.
【变式1】如图,已知在△ABC中,∠B<∠C,AD平分
∠BAC,E为线段AD(除去端,点A,D)上一动点,EF
⊥BC于点F.
(1)若∠B=40°,∠DEF=10°,则∠C的度数为
(2)当E在AD上移动时,∠B,∠C,∠DEF之间存在
怎样的数量关系?请写出这个数量关系,并说明
理由
解:(1)60°;
(2)∠DEF-(∠C-∠B.
理由如下:.EF⊥BC,
∴.∠DEF=90°-∠EDF.
.‘AD平分∠BAC,
:∠BAD=∠BAC
∠EDF=∠B+∠BAD=∠B+2∠BAC
又.∠BAC=180°-∠B-∠C,
∴∠EDF=∠B+2(180-∠B-∠C)=90°+
∴∠DBF=90-(90+2∠B-2∠C)=(∠C
∠B).
【变式2】如图,在△ABC中,∠1=∠2,∠C>∠B,E
为AD延长线上一点,且EF⊥BC于点F.
(1)若∠B=40°,∠C=60,则∠DEF的度数为
(2)由解答(1)的过程,试探索∠DEF与∠B,∠C的
数量关系,并说明理由,
解:(1)10°;
(2)∠DEF=(∠C-∠B.理由如下:
F
B
.∠BAC=180°-∠B-∠C,∠1=
∠2,
∴∠2=2180°-∠B-∠C.
∴∠ADC=180°-∠C-∠2=90-3∠C+3∠B,
∠EDF=∠ADC=90-2∠C+2
∠B,
∴.∠DEF=90°-∠EDF=90°-(90°-2∠C+
2∠B)=(∠C-∠B.
类型①三角形中两条高的夹角
1.如图,在△ABC中,CD,BE分别是AB,AC边上的
高,BE,CD相交于点O.
(1)若∠ABC=50°,∠ACB=60°,求∠BO℃的度数;
(2)求证:∠BOC+∠A=180°.
解:(1).CD⊥AB,BE⊥AC,
.∠BDC=∠BEC=90°
.∠ABC=50°,∠ACB=60°,
.∠BCD=90°-50°=40°,
∠CBE=90°-60°=30°,
.∠BOC=180°-∠BCD-∠CBE=110°;
(2).∠BDC=∠BEC=90°,
.∠ABE=90°-∠A,
∴.∠BOC=∠ABE+∠BDC=90°-∠A+90°=
180°-∠A,
.∴.∠BOC+∠A=180°.
类型②三角形同一条边上的高与角平分线
的夹角
2.如图,AD,AE分别是△ABC的角平分线和高.
(1)若∠B=50°,∠C=60°,则∠DAE=
(2)若∠C>∠B,猜想∠DAE与∠C-∠B之间的
数量关系,并加以证明.
解:(1)5°;
(2)∠DAE=2(∠C-∠B).
证明如下:.'AE是△ABC的高,
DE
∴.∠AEC=90°,.∴.∠EAC=90°-∠C
AD是△ABC的角平分线,
∠DAC=2∠BAC.
.∠BAC=180°-∠B-∠C,
÷∠DAC=2(180°-∠B-∠C)=90-2∠B
∠C,
1
∠B
∴.∠DAE=∠DAC-∠EAC=90°-1
2∠C-(90°-∠C)=2(∠C-∠B.
【变式1】如图,已知在△ABC中,∠B<∠C,AD平分
∠BAC,E为线段AD(除去端,点A,D)上一动点,EF
⊥BC于点F.
(1)若∠B=40°,∠DEF=10°,则∠C的度数为
(2)当E在AD上移动时,∠B,∠C,∠DEF之间存在
怎样的数量关系?请写出这个数量关系,并说明
理由
解:(1)60°;
(2)∠DEF-(∠C-∠B.
理由如下:.EF⊥BC,
∴.∠DEF=90°-∠EDF.
.‘AD平分∠BAC,
:∠BAD=∠BAC
∠EDF=∠B+∠BAD=∠B+2∠BAC
又.∠BAC=180°-∠B-∠C,
∴∠EDF=∠B+2(180-∠B-∠C)=90°+
∴∠DBF=90-(90+2∠B-2∠C)=(∠C
∠B).
【变式2】如图,在△ABC中,∠1=∠2,∠C>∠B,E
为AD延长线上一点,且EF⊥BC于点F.
(1)若∠B=40°,∠C=60,则∠DEF的度数为
(2)由解答(1)的过程,试探索∠DEF与∠B,∠C的
数量关系,并说明理由,
解:(1)10°;
(2)∠DEF=(∠C-∠B.理由如下:
F
B
.∠BAC=180°-∠B-∠C,∠1=
∠2,
∴∠2=2180°-∠B-∠C.
∴∠ADC=180°-∠C-∠2=90-3∠C+3∠B,
∠EDF=∠ADC=90-2∠C+2
∠B,
∴.∠DEF=90°-∠EDF=90°-(90°-2∠C+
2∠B)=(∠C-∠B.
