2022-2023鲁教版数学八年级上册期中模拟练习题(含解析)
文档属性
| 名称 | 2022-2023鲁教版数学八年级上册期中模拟练习题(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 70.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-24 00:00:00 | ||
图片预览




文档简介
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
2022-2023鲁教版数学八年级上册期中模拟练习题
一、选择题
下列各式:,,,属于正确的因式分解的有( )
A. 个 B. 个 C. 个 D. 个
多项式的各项公因式是( )
A. B. C. D.
下列等式中,从左到右的变形属于因式分解的是( )
A. B.
C. D.
如图是我市月日至日一周内“日平均气温变化统计图”,在这组数据中,众数和中位数分别是( )
A. ,
B. ,
C. ,
D. ,
我国古代著作四元玉鉴记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为文.如果每株椽的运费是文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问文能买多少株椽?设这批椽的数量为株,则符合题意的方程是( )
A. B.
C. D.
解分式方程,去分母得( )
A. B.
C. D.
已知,,为三边,且满足,则是( )
A. 直角三角形 B. 等边三角形 C. 等腰三角形 D. 不能确定
若分式中的,的值同时扩大到原来的倍,则分式的值( )
A. 变为原来的倍 B. 变为原来的 C. 变为原来的 D. 变为原来的
甲,乙,丙三种糖果售价分别为每千克元,元,元,若将甲种,乙种,丙种混在一起,则售价应定为每千克( )
A. 元 B. 元 C. 元 D. 元
能被下列哪个数整除 ( )
A. B. C. D.
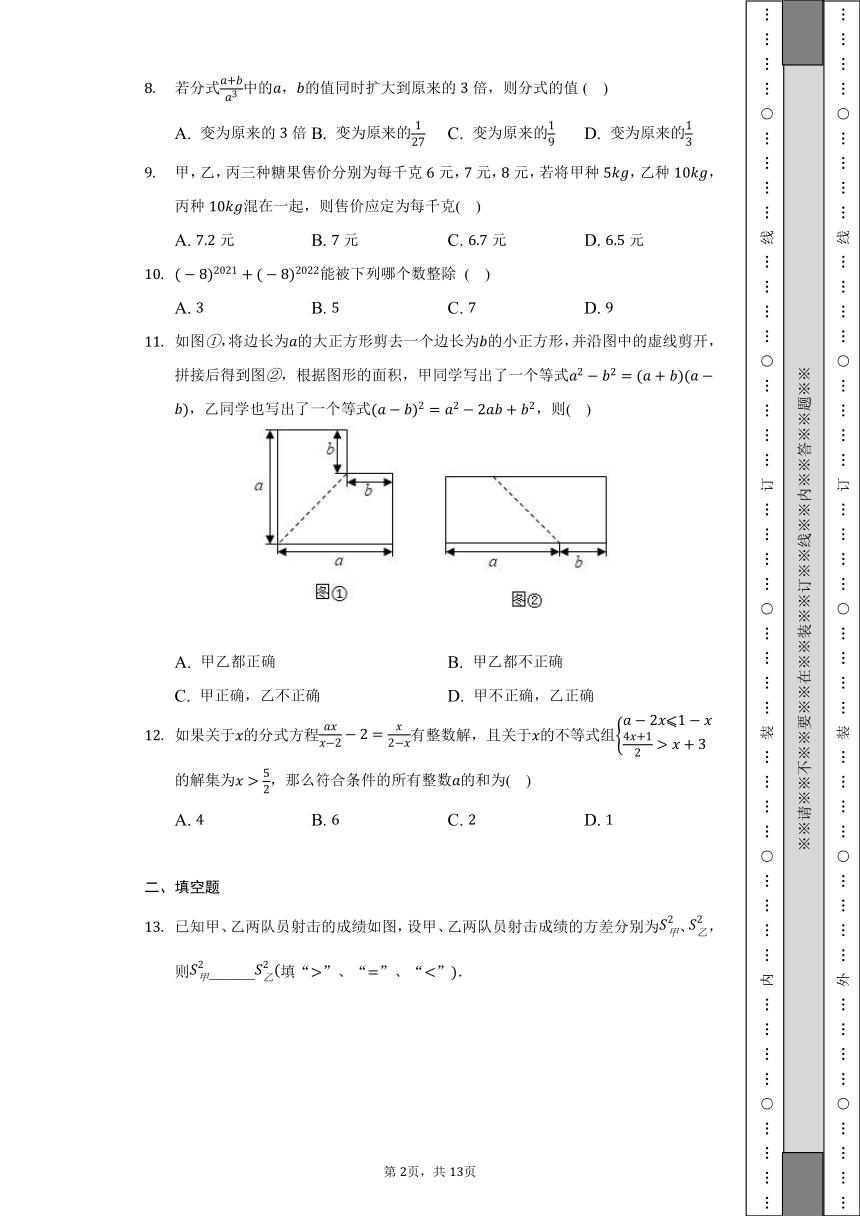
如图,将边长为的大正方形剪去一个边长为的小正方形,并沿图中的虚线剪开,拼接后得到图,根据图形的面积,甲同学写出了一个等式,乙同学也写出了一个等式,则( )
A. 甲乙都正确 B. 甲乙都不正确
C. 甲正确,乙不正确 D. 甲不正确,乙正确
如果关于的分式方程有整数解,且关于的不等式组的解集为,那么符合条件的所有整数的和为( )
A. B. C. D.
二、填空题
已知甲、乙两队员射击的成绩如图,设甲、乙两队员射击成绩的方差分别为、,则______填“”、“”、“”.
一组数据,,的平均数为,另一组数据,,,,的众数为,则数据,,,,的中位数为 .
若关于的方程无解,则的值是 .
小明用计算一组数据的方差,那么 __ ____ .
关于的分式方程的解为正数,则的取值范围是 .
已知,则 .
三、计算题
计算:
.
解答题
20.先化简,再求值.
,请从不等式组的整数解中选择一个你喜欢的求值.
21.
某市为治理污水,需要铺设一段全长为的污水排放管道,为了尽量减少施工对城市交通所造成的影响,实际施工时每天的工效比原计划增加,结果提前天完成这一任务,实际每天铺设多长管道?
22.
为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买种图书花费了元,购买种图书花费了元,种图书的单价是种图书的倍,购买种图书的数量比种图书多本.
求和两种图书的单价;
书店在“世界读书日”进行打折促销活动,所有图书都按折销售学校当天购买了种图书本和种图书本,共花费多少元?
23.
阅读下面材料,解答后面的问题.
解方程:.
解:设,则原方程可化为,方程两边同时乘,得,解得,.
经检验,,都是方程的解.
当时,,解得当时,,解得.
经检验,,都是原分式方程的解.原分式方程的解为,.
上述这种解分式方程的方法称为换元法.
问题:
若在方程中,设,则原方程可化为
若在方程中,设,则原方程可化为
模仿上述换元法解方程:.
24.
新冠肺炎疫情暴发后,某医疗设备公司紧急复工,但受疫情影响,医用防护服生产车间仍有人不能到厂生产为了应对疫情,已复产的工人加班生产,由原来每天工作小时增加到小时,每小时完成的工作量不变原来每天能生产防护服套,现在每天能生产防护服套.
求原来生产防护服的工人有多少人.
复工天后,未到的工人同时到岗加入生产,每天生产时间仍然为小时公司决定将复工后生产的防护服套捐献给某地,则至少还需要生产多少天才能完成任务
答案和解析
1.【答案】
【解析】
【分析】
本题主要考查的是因式分解的意义,把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫做分解因式.根据因式分解的意义对各小题进行分析即可.
【解答】
解:,故原题因式分解错误;
,不是因式分解,故错误;
,正确;
等式左边不是多项式,右边不是几个整式的积的形式,不是因式分解,
所以属于正确的因式分解的有个.
故选A.
2.【答案】
【解析】
【分析】
本题主要考查公因式的定义,找公因式的要点是:
公因式的系数是多项式各项系数的最大公约数;
字母取各项都含有的相同字母;
相同字母的指数取次数最低的.
根据公因式定义,对多项式各项整理即可选出公因式.
【解答】
解:,
是公因式,
故选D.
3.【答案】
【解析】
【分析】
本题考查了因式分解的定义:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解.
根据定义分析可得.
【解答】
解:由因式分解的定义可知选项中的变形是因式分解,
故选B.
4.【答案】
【解析】
【分析】
本题考查了众数、中位数以及折线统计图 ,掌握众数、中位数的定义是解题的关键.
根据折线统计图以及众数、中位数的定义进行选择即可.
【解答】
解:这个数据分别为,,,,,,,
从小到大排列为,,,,,,,
处于中间的数是,所以中位数是,
出现两次,出现次数最多,所以众数是,
所以众数和中位数分别是,,
故选C.
5.【答案】
【解析】
【分析】
本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解题的关键.
根据单价总价数量,结合少拿一株椽后剩下的椽的运费恰好等于一株椽的价钱,即可得出关于的分式方程,此题得解.
【解答】
解:依题意,得:.
故选:.
6.【答案】
【解析】
【分析】
此题主要考查了解分式方程的去分母步骤.
分式方程变形后,两边乘以最简公分母得到结果,即可作出判断.
【解答】
解:分式方程整理得:,
去分母得:,
故选A.
7.【答案】
【解析】解:,
,即,
,
或,
是等腰三角形,
故选:.
将已知式子因式分解为,则有或,即可判断三角形的形状.
本题考查因式分解的应用;理解题意,将已知式子因式分解,再由整式的性质进行求解是解题的关键.
8.【答案】
【解析】,则分式的值变为原来的.
9.【答案】
【解析】解:根据题意售价应该定为元千克,
故选:.
平均数的计算方法是求出所有糖果的总钱数,然后除以糖果的总质量.
本题考查的是加权平均数的求法.本题易出现的错误是求、、这四个数的平均数,对平均数的理解不正确.
10.【答案】
【解析】解:,
能被整除;
故选:.
将已知式子提取公因数即可求解;
本题考查有理数的乘方及提取公因式法分解因式;能够将较大数提取公因数是解题的关键.
11.【答案】
【解析】解:图面积为:,
图的面积为:,
,
甲同学写得正确,
故选:.
分别表示出两个图形的面积,再根据面积相等得出等式即可.
考查平方差公式的几何背景,用面积相等得出等式是常用的方法.
12.【答案】
【解析】
【分析】
本题考查了分式方程的解以及解一元一次不等式,根据分式方程的解为整数结合不等式组的解集为,得出的取值范围是解题的关键.
根据分式方程的解为整数即可得出的可能的值,根据不等式组的解集为,即可得出的范围,找出符合题意的所有的整数,将其相加即可得出结论.
【解答】
解:,
有整数解,
或或
或或或或或
或或或或;
解得:
解集为
值为或或或,
则.
故选C.
13.【答案】
【解析】解:甲射击的成绩为:,,,,,,,,,,
乙射击的成绩为:,,,,,,,,,,
则,
,
;
;
,
,
故答案为:.
先计算两组数据的平均数,再计算它们的方差,即可得出答案.
此题主要考查了平均数及方差的知识.方差的定义:一般地设个数据,,,的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
14.【答案】
【解析】
【分析】
本题考查了平均数、众数及中位数的定义,解题的关键是正确利用其定义求得未知数的值.
先根据平均数求得的值,再根据众数求得的值,最后根据中位数的定义求解.
【解答】
解:一组数据,,的平均数为,
,
解得,
数据,,,,的众数为,
,
把数据,,,,按从小到大的顺序排列为:,,,,,
中位数为.
故答案为:.
15.【答案】
【解析】分析:本题考查分式方程的解法此方程去分母后为一元一次方程,有唯一的解,由原方程无解可知一元一次方程的解为原方程的增根,根据增根的定义得,求得增根再代入一元一次方程即可.
解: ,
分式方程去分母,得,即,
由分式方程无解,得到,即,
将代人,得,
解得.
故答案为.
16.【答案】
【解析】
【分析】
本题考查的是方差的计算、平均数的概念,掌握方差的计算公式:是解题的关键.
根据方差计算公式确定这组数据的平均数,计算即可.
【解答】
解:,
这组数据的平均数是,
,
故答案为:.
17.【答案】且
【解析】略
18.【答案】
【解析】.
19.【答案】解:原式
原式
原式.
【解析】略
21.【答案】解:
,
由不等式组,得,
的整数解有,,,,,,
,,,
当时,原式.
【解析】本题考查分式的化简求值、一元一次不等式组的整数解,解答本题的关键是明确分式化简求值的方法.根据分式的除法和加法可以化简题目中的式子,然后由不等式组,可以求得的取值范围,再从中选取一个使得原分式有意义的整数代入化简后的式子即可解答本题.
21.【答案】解:设原计划每天铺设米,依题意得:
,
解得:,
经检验是原方程式的根,
实际每天铺设米.
答:实际每天铺设米长管道.
【解析】首先设原计划每天铺设米,则实际每天铺设米,由题意找出等量关系:原计划的工作时间实际的工作时间,
然后列出方程可求出结果,最后检验并作答.
本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.本题应用了工作时间工作总量工效这个等量关系.
22.【答案】解:设种图书的单价为元,则种图书的单价为元,
依题意,得:,
解得:,
经检验,是所列分式方程的解,且符合题意,
.
答:种图书的单价为元,种图书的单价为元.
元.
答:共花费元.
【解析】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
设种图书的单价为元,则种图书的单价为元,根据数量总价单价,结合花元购买的种图书比花元购买的种图书多本,即可得出关于的分式方程,解之经检验后即可得出结论;
根据总价单价数量,即可求出结论.
23.【答案】解:
原方程可化为,
设,
则原方程可化为.
方程两边同时乘,得,解得,.
经检验,,都是方程的解.
当时,,该方程无解,
当时,,解得,
经检验,是原分式方程的解.
原分式方程的解为.
【解析】略
24.【答案】解:设原来生产防护服的工人有人.
由题意得,
解得.
经检验,是分式方程的解,且符合题意.
答:原来生产防护服的工人有人.
设还需要生产天才能完成任务.
套,
即每人每小时生产套防护服.
由题意得,
解得
答:至少还需要生产天才能完成任务.
【解析】略
第2页,共2页
第1页,共1页
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
2022-2023鲁教版数学八年级上册期中模拟练习题
一、选择题
下列各式:,,,属于正确的因式分解的有( )
A. 个 B. 个 C. 个 D. 个
多项式的各项公因式是( )
A. B. C. D.
下列等式中,从左到右的变形属于因式分解的是( )
A. B.
C. D.
如图是我市月日至日一周内“日平均气温变化统计图”,在这组数据中,众数和中位数分别是( )
A. ,
B. ,
C. ,
D. ,
我国古代著作四元玉鉴记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为文.如果每株椽的运费是文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问文能买多少株椽?设这批椽的数量为株,则符合题意的方程是( )
A. B.
C. D.
解分式方程,去分母得( )
A. B.
C. D.
已知,,为三边,且满足,则是( )
A. 直角三角形 B. 等边三角形 C. 等腰三角形 D. 不能确定
若分式中的,的值同时扩大到原来的倍,则分式的值( )
A. 变为原来的倍 B. 变为原来的 C. 变为原来的 D. 变为原来的
甲,乙,丙三种糖果售价分别为每千克元,元,元,若将甲种,乙种,丙种混在一起,则售价应定为每千克( )
A. 元 B. 元 C. 元 D. 元
能被下列哪个数整除 ( )
A. B. C. D.
如图,将边长为的大正方形剪去一个边长为的小正方形,并沿图中的虚线剪开,拼接后得到图,根据图形的面积,甲同学写出了一个等式,乙同学也写出了一个等式,则( )
A. 甲乙都正确 B. 甲乙都不正确
C. 甲正确,乙不正确 D. 甲不正确,乙正确
如果关于的分式方程有整数解,且关于的不等式组的解集为,那么符合条件的所有整数的和为( )
A. B. C. D.
二、填空题
已知甲、乙两队员射击的成绩如图,设甲、乙两队员射击成绩的方差分别为、,则______填“”、“”、“”.
一组数据,,的平均数为,另一组数据,,,,的众数为,则数据,,,,的中位数为 .
若关于的方程无解,则的值是 .
小明用计算一组数据的方差,那么 __ ____ .
关于的分式方程的解为正数,则的取值范围是 .
已知,则 .
三、计算题
计算:
.
解答题
20.先化简,再求值.
,请从不等式组的整数解中选择一个你喜欢的求值.
21.
某市为治理污水,需要铺设一段全长为的污水排放管道,为了尽量减少施工对城市交通所造成的影响,实际施工时每天的工效比原计划增加,结果提前天完成这一任务,实际每天铺设多长管道?
22.
为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买种图书花费了元,购买种图书花费了元,种图书的单价是种图书的倍,购买种图书的数量比种图书多本.
求和两种图书的单价;
书店在“世界读书日”进行打折促销活动,所有图书都按折销售学校当天购买了种图书本和种图书本,共花费多少元?
23.
阅读下面材料,解答后面的问题.
解方程:.
解:设,则原方程可化为,方程两边同时乘,得,解得,.
经检验,,都是方程的解.
当时,,解得当时,,解得.
经检验,,都是原分式方程的解.原分式方程的解为,.
上述这种解分式方程的方法称为换元法.
问题:
若在方程中,设,则原方程可化为
若在方程中,设,则原方程可化为
模仿上述换元法解方程:.
24.
新冠肺炎疫情暴发后,某医疗设备公司紧急复工,但受疫情影响,医用防护服生产车间仍有人不能到厂生产为了应对疫情,已复产的工人加班生产,由原来每天工作小时增加到小时,每小时完成的工作量不变原来每天能生产防护服套,现在每天能生产防护服套.
求原来生产防护服的工人有多少人.
复工天后,未到的工人同时到岗加入生产,每天生产时间仍然为小时公司决定将复工后生产的防护服套捐献给某地,则至少还需要生产多少天才能完成任务
答案和解析
1.【答案】
【解析】
【分析】
本题主要考查的是因式分解的意义,把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫做分解因式.根据因式分解的意义对各小题进行分析即可.
【解答】
解:,故原题因式分解错误;
,不是因式分解,故错误;
,正确;
等式左边不是多项式,右边不是几个整式的积的形式,不是因式分解,
所以属于正确的因式分解的有个.
故选A.
2.【答案】
【解析】
【分析】
本题主要考查公因式的定义,找公因式的要点是:
公因式的系数是多项式各项系数的最大公约数;
字母取各项都含有的相同字母;
相同字母的指数取次数最低的.
根据公因式定义,对多项式各项整理即可选出公因式.
【解答】
解:,
是公因式,
故选D.
3.【答案】
【解析】
【分析】
本题考查了因式分解的定义:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解.
根据定义分析可得.
【解答】
解:由因式分解的定义可知选项中的变形是因式分解,
故选B.
4.【答案】
【解析】
【分析】
本题考查了众数、中位数以及折线统计图 ,掌握众数、中位数的定义是解题的关键.
根据折线统计图以及众数、中位数的定义进行选择即可.
【解答】
解:这个数据分别为,,,,,,,
从小到大排列为,,,,,,,
处于中间的数是,所以中位数是,
出现两次,出现次数最多,所以众数是,
所以众数和中位数分别是,,
故选C.
5.【答案】
【解析】
【分析】
本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解题的关键.
根据单价总价数量,结合少拿一株椽后剩下的椽的运费恰好等于一株椽的价钱,即可得出关于的分式方程,此题得解.
【解答】
解:依题意,得:.
故选:.
6.【答案】
【解析】
【分析】
此题主要考查了解分式方程的去分母步骤.
分式方程变形后,两边乘以最简公分母得到结果,即可作出判断.
【解答】
解:分式方程整理得:,
去分母得:,
故选A.
7.【答案】
【解析】解:,
,即,
,
或,
是等腰三角形,
故选:.
将已知式子因式分解为,则有或,即可判断三角形的形状.
本题考查因式分解的应用;理解题意,将已知式子因式分解,再由整式的性质进行求解是解题的关键.
8.【答案】
【解析】,则分式的值变为原来的.
9.【答案】
【解析】解:根据题意售价应该定为元千克,
故选:.
平均数的计算方法是求出所有糖果的总钱数,然后除以糖果的总质量.
本题考查的是加权平均数的求法.本题易出现的错误是求、、这四个数的平均数,对平均数的理解不正确.
10.【答案】
【解析】解:,
能被整除;
故选:.
将已知式子提取公因数即可求解;
本题考查有理数的乘方及提取公因式法分解因式;能够将较大数提取公因数是解题的关键.
11.【答案】
【解析】解:图面积为:,
图的面积为:,
,
甲同学写得正确,
故选:.
分别表示出两个图形的面积,再根据面积相等得出等式即可.
考查平方差公式的几何背景,用面积相等得出等式是常用的方法.
12.【答案】
【解析】
【分析】
本题考查了分式方程的解以及解一元一次不等式,根据分式方程的解为整数结合不等式组的解集为,得出的取值范围是解题的关键.
根据分式方程的解为整数即可得出的可能的值,根据不等式组的解集为,即可得出的范围,找出符合题意的所有的整数,将其相加即可得出结论.
【解答】
解:,
有整数解,
或或
或或或或或
或或或或;
解得:
解集为
值为或或或,
则.
故选C.
13.【答案】
【解析】解:甲射击的成绩为:,,,,,,,,,,
乙射击的成绩为:,,,,,,,,,,
则,
,
;
;
,
,
故答案为:.
先计算两组数据的平均数,再计算它们的方差,即可得出答案.
此题主要考查了平均数及方差的知识.方差的定义:一般地设个数据,,,的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
14.【答案】
【解析】
【分析】
本题考查了平均数、众数及中位数的定义,解题的关键是正确利用其定义求得未知数的值.
先根据平均数求得的值,再根据众数求得的值,最后根据中位数的定义求解.
【解答】
解:一组数据,,的平均数为,
,
解得,
数据,,,,的众数为,
,
把数据,,,,按从小到大的顺序排列为:,,,,,
中位数为.
故答案为:.
15.【答案】
【解析】分析:本题考查分式方程的解法此方程去分母后为一元一次方程,有唯一的解,由原方程无解可知一元一次方程的解为原方程的增根,根据增根的定义得,求得增根再代入一元一次方程即可.
解: ,
分式方程去分母,得,即,
由分式方程无解,得到,即,
将代人,得,
解得.
故答案为.
16.【答案】
【解析】
【分析】
本题考查的是方差的计算、平均数的概念,掌握方差的计算公式:是解题的关键.
根据方差计算公式确定这组数据的平均数,计算即可.
【解答】
解:,
这组数据的平均数是,
,
故答案为:.
17.【答案】且
【解析】略
18.【答案】
【解析】.
19.【答案】解:原式
原式
原式.
【解析】略
21.【答案】解:
,
由不等式组,得,
的整数解有,,,,,,
,,,
当时,原式.
【解析】本题考查分式的化简求值、一元一次不等式组的整数解,解答本题的关键是明确分式化简求值的方法.根据分式的除法和加法可以化简题目中的式子,然后由不等式组,可以求得的取值范围,再从中选取一个使得原分式有意义的整数代入化简后的式子即可解答本题.
21.【答案】解:设原计划每天铺设米,依题意得:
,
解得:,
经检验是原方程式的根,
实际每天铺设米.
答:实际每天铺设米长管道.
【解析】首先设原计划每天铺设米,则实际每天铺设米,由题意找出等量关系:原计划的工作时间实际的工作时间,
然后列出方程可求出结果,最后检验并作答.
本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.本题应用了工作时间工作总量工效这个等量关系.
22.【答案】解:设种图书的单价为元,则种图书的单价为元,
依题意,得:,
解得:,
经检验,是所列分式方程的解,且符合题意,
.
答:种图书的单价为元,种图书的单价为元.
元.
答:共花费元.
【解析】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.
设种图书的单价为元,则种图书的单价为元,根据数量总价单价,结合花元购买的种图书比花元购买的种图书多本,即可得出关于的分式方程,解之经检验后即可得出结论;
根据总价单价数量,即可求出结论.
23.【答案】解:
原方程可化为,
设,
则原方程可化为.
方程两边同时乘,得,解得,.
经检验,,都是方程的解.
当时,,该方程无解,
当时,,解得,
经检验,是原分式方程的解.
原分式方程的解为.
【解析】略
24.【答案】解:设原来生产防护服的工人有人.
由题意得,
解得.
经检验,是分式方程的解,且符合题意.
答:原来生产防护服的工人有人.
设还需要生产天才能完成任务.
套,
即每人每小时生产套防护服.
由题意得,
解得
答:至少还需要生产天才能完成任务.
【解析】略
第2页,共2页
第1页,共1页
同课章节目录
