湘教版数学七年级上册 第1章 有理数 小结与复习课件(共41张PPT)
文档属性
| 名称 | 湘教版数学七年级上册 第1章 有理数 小结与复习课件(共41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-24 21:20:43 | ||
图片预览










文档简介
(共41张PPT)
第一章
有理数
小结与复习
1
2
3
目录
CONTENTS
要点梳理
4
考点讲练
当堂练习
课堂小结
要 点 梳 理
1.有理数可以如何分类?
2.怎样画一条数轴?怎样用数轴上的点来表示一个有理数?
3.如何求一个数的相反数?如何求一个数的绝对值?
4.怎样比较有理数的大小?
5.怎样进行有理数的加、减、乘、除、乘方运算?
回顾
本章知识结构
2.用正、负数表示具有相反意义的量.
1.大于0的自然数和分数(或小数)就是正数;
在正数前面加上符号“-”号的数叫做负数;
0既不是正数,也不是负数;正数和0统称为非负数.
一、正数和负数
二、有理数
1.正整数、零和负整数统称为整数;
正分数和负分数统称为分数;
整数和分数统称为有理数.
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
有理数
正整数
正分数
整数
分数
零
负整数
自然数
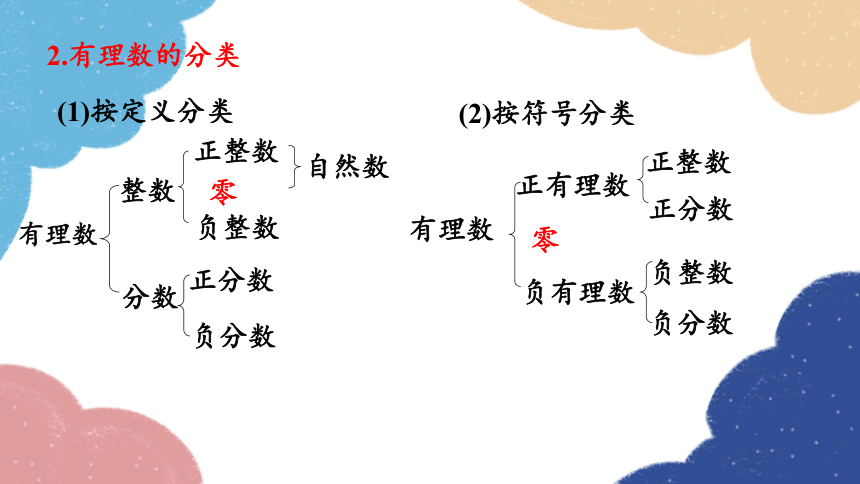
2.有理数的分类
负分数
(1)按定义分类
(2)按符号分类
3.数轴
(4)规定了原点、正方向、单位长度的直线叫做数轴.
(5)任何一个有理数都可以用数轴上唯一的一个点 来表示.
(1)画一条直线(通常把它水平放置),在直线上取一点O,把点O叫做原点,用原点表示数0.
(2)选定直线的正方向(标上箭头).
(3)选择适当的长度为单位长度.
4.相反数
(1)两个数只有符号不同,那么其中一个数叫做
另一个数的相反数,也称这两个数互为相反数.
0的相反数是0.
(2)表示互为相反数的两个数的点,在数轴上分别
位于原点的两侧,并且与原点的距离相等.
5.绝对值
(1)一个数的绝对值等于数轴上表示这个数的点与原点的距离.数a的绝对值,记作|a|.
(2)正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0.互为相反数的两个数的绝对值相等.
(3)一般地,如果a表示一个数,则
①当a是正数时,|a|=a;
②当a=0时,|a|=0;
③当a是负数时,|a|=-a.
6.倒数
如果两个数的乘积等于1,我们把其中一个数叫做另一个数的倒数,也称它们互为倒数.0没有倒数.
7.有理数大小的比较
(2) 在以向右为正方向的数轴上,右边的点表示的数比左边的点表示的数大.
(1) 正数大于负数,0大于负数;
两个负数,绝对值大的反而小.
三、有理数的运算
1.有理数的加法
(1)加法法则
两个负数相加,结果是负数,并且把它们的绝对值相加.
异号两数相加,当它们的绝对值不相等时,取绝对值较大的加数的符号,并且用较大的绝对值减去较小的绝对值.
(2)加法的运算律
交换律 a+b=b+a
结合律a+b+c=(a+b)+c=a+(b+c)
互为相反数的两个数相加得0;一个数与0相加,仍得这个数.
2.有理数的减法
减法法则:
减去一个数,等于加上这个数的相反数.
3.有理数的乘法
(1)乘法法则
异号两数相乘得负数,并且把绝对值相乘.
任何数与0相乘,仍得0.
同号两数相乘得正数,并且把绝对值相乘.
(2)几个不等于0的数相乘,当负因数有奇数个时,积为负;当负因数有偶数个时,积为正.
(2)同号两数相除得正数,异号两数相除得负数,并把它们的绝对值相除;0除以任何一个不等于0的数都得0.
4.有理数的除法
(3)乘法的运算律
(3)除以一个不为0的数,等于乘以这个数的倒数.
乘法交换律:
乘法结合律
乘法的分配律
(1)对于两个有理数a,b,其中b≠0,如果有一个有理数c,使得cb=a,那么规定a÷b=c,且把c叫做a除以b的商.
5.有理数的乘方
(1)求n个相同因数的积的运算,叫做乘方.乘方的结果叫做幂.在an中,a叫做底数,n叫做指数.
幂
指数
底数
(2)正数的任何正整数次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0的任何正整数次幂都是0.
特别地,a2通常读作a的平方,a3通常读作a的立方.
a1规定为a.
(1)先算乘方,再算乘除,最后算加减;
(2)同级运算,从左到右进行;
(3)如有括号,先进行括号里面的运算,按小括号、中括号、大括号依次进行.
6.有理数的混合运算
四、科学记数法
(2)n为原数的整数位减去1.
(1)把一个绝对值大于10的数记做 a×10n的形式,其中a是整数数位只有一位的数(即1≤|a|<10),这种记数法叫做科学记数法.
注意
考 点 讲 练
考点一 正、负数的意义
例1 如果-4米表示向东走4米,那么向西走2米记作_____.
+2米
【解析】根据题意,可知向东记为负,向西记为正, 故向西走2米记做+2米.
【方法总结】根据相反意义合理使用正、负数对实际问题进行表示.一般情况下,把向北(东)、上升、增加、收入等规定为正,把它们的相反意义规定为负.
注意带单位
针对训练
1.下列语句中,含有相反意义的两个量是( )
A.盈利1千元和收入2千元
B.上升8米和后退8米
C.存入1千元和取出2千元
D.超过2厘米和上涨2厘米
C
-8
2.上升9记作+9,那么下降8记作____.
考点二 正、负数的概念
例2 判断:
①不带“-”号的数都是正数 ( )
④一个有理数不是正数就是负数 ( )
⑤ 0℃表示没有温度 ( )
②如果a是正数,那么-a一定是负数( )
③不存在既不是正数,也不是负数的数( )
×
×
×
×
√
【解析】①0不带“-”号,但0不是正数,故①错误;②正数的相反数是负数,故②正确;③同①,故③错误;④同③,故④错误;⑤0℃并不是表示没有温度,它是介于正温度与负温度之间,故⑤错误.
方法总结
0既不是正数也不是负数,0的相反数是它本身.
0不仅能表示没有,而且表示正、负之间的分界值.
考点三 有理数的分类
例3 将下列各数分别填入下列相应的圈内:
3.5
|-2|
0
-3.5
-2
-1
3
5
-
1
3
0.5
, , , , , , ,
正数
负数
整数
分数
3.5,
|-2|,
0.5
-3.5
,-2
,-1
3
5
,-
1
3
0
,|-2|
,-2
3.5,
,0.5
-3.5,
-1
3
5
,-
1
3
针对训练
【解析】负分数不仅是负数而且是分数,注意小数也属于分数.故只有2个.
2
3.在+3.5,0,11,-2, ,-0.7 中,负分数有 个.
考点四 相反数、倒数、绝对值
例4 填表
3.5
|-2|
0
-3.5
-2
-1
3
5
-
1
3
0.5
数
相反数
倒数
绝对值
-3.5
-2
0
3.5
2
-0.5
1
3
5
1
3
3.5
2
0
3.5
2
0.5
1
3
5
1
3
-3
没有
-0.5
2
0.5
-
2
7
2
7
-
5
8
1
1
3
-3
–5的绝对值是 .
5
针对训练
4. 的倒数是 ; 的相反数是 ;
-
1
3
考点五 数轴
例5 请你将下面的数在数轴上表示出来
3.5
|-2|
0
-3.5
-2
0.5
, , , , , , ,
-1
3
5
-
1
3
解:表示如下
针对训练
5.在数轴上,点A所表示的数为2,那么到点A的距离等于3个单位长度的点所表示的数是________.
-1或3
考点六 有理数比较大小
例6 请你将下面的数用“>”连接起来
解法一:将各数在数轴上表示出来,右边的大于左边的,然后从大到小排列
解法二:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
6.某日零点,北京、上海、宁夏的气温分别是﹣4℃、5℃、6℃、﹣8℃,当时这四个城市中,气温最低的是 ( )
A.北京 B.上海 C.重庆 D.宁夏
针对训练
D
考点七 科学记数法
例7 将数13 445 000 000 000km用科学记数法表示___________m.
1.3445×1016
注意统一单位
7.2016年末上海市常住人口总数为2615.27万人,用科学记数法表示为 人.
2.61527×107
针对训练
考点八 有理数的运算
例8 计算
(1)
(2)
(3)
(4)
1.把减法转化为加法时,要注意符号.
2.对几个有理数相加减的题目,要注意观察,将哪些数放在一起会使计算简便
解:(1)
(2)
注意符号问题
(3)
先确定商的符号,再把绝对值相除
注意:1.底数是带分数时,要先将带分数化成假分数.
2.区分-24与(-2)4.
(4)
针对训练
9.计算
(1)
(2)
(3)
(4)
答案:(1)-17
(2)33
(3)-3.3
课 堂 小 结
整数
分数
负分数
正分数
正有理数
负有理数
0
有理数
0
正整数
负整数
有
理
数
数轴
比较大小
相反数
点与数的对应
绝对值
倒数
科学记数法
有理数运算
减法
加法
乘法
乘方
除法
交换律、结合律
法则
运算律
转 化
加法
乘法
混
合
运
算
按
顺
序
进
行
转 化
交换律、结合律、分配律
thanks for your coming
第一章
有理数
小结与复习
1
2
3
目录
CONTENTS
要点梳理
4
考点讲练
当堂练习
课堂小结
要 点 梳 理
1.有理数可以如何分类?
2.怎样画一条数轴?怎样用数轴上的点来表示一个有理数?
3.如何求一个数的相反数?如何求一个数的绝对值?
4.怎样比较有理数的大小?
5.怎样进行有理数的加、减、乘、除、乘方运算?
回顾
本章知识结构
2.用正、负数表示具有相反意义的量.
1.大于0的自然数和分数(或小数)就是正数;
在正数前面加上符号“-”号的数叫做负数;
0既不是正数,也不是负数;正数和0统称为非负数.
一、正数和负数
二、有理数
1.正整数、零和负整数统称为整数;
正分数和负分数统称为分数;
整数和分数统称为有理数.
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
有理数
正整数
正分数
整数
分数
零
负整数
自然数
2.有理数的分类
负分数
(1)按定义分类
(2)按符号分类
3.数轴
(4)规定了原点、正方向、单位长度的直线叫做数轴.
(5)任何一个有理数都可以用数轴上唯一的一个点 来表示.
(1)画一条直线(通常把它水平放置),在直线上取一点O,把点O叫做原点,用原点表示数0.
(2)选定直线的正方向(标上箭头).
(3)选择适当的长度为单位长度.
4.相反数
(1)两个数只有符号不同,那么其中一个数叫做
另一个数的相反数,也称这两个数互为相反数.
0的相反数是0.
(2)表示互为相反数的两个数的点,在数轴上分别
位于原点的两侧,并且与原点的距离相等.
5.绝对值
(1)一个数的绝对值等于数轴上表示这个数的点与原点的距离.数a的绝对值,记作|a|.
(2)正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0.互为相反数的两个数的绝对值相等.
(3)一般地,如果a表示一个数,则
①当a是正数时,|a|=a;
②当a=0时,|a|=0;
③当a是负数时,|a|=-a.
6.倒数
如果两个数的乘积等于1,我们把其中一个数叫做另一个数的倒数,也称它们互为倒数.0没有倒数.
7.有理数大小的比较
(2) 在以向右为正方向的数轴上,右边的点表示的数比左边的点表示的数大.
(1) 正数大于负数,0大于负数;
两个负数,绝对值大的反而小.
三、有理数的运算
1.有理数的加法
(1)加法法则
两个负数相加,结果是负数,并且把它们的绝对值相加.
异号两数相加,当它们的绝对值不相等时,取绝对值较大的加数的符号,并且用较大的绝对值减去较小的绝对值.
(2)加法的运算律
交换律 a+b=b+a
结合律a+b+c=(a+b)+c=a+(b+c)
互为相反数的两个数相加得0;一个数与0相加,仍得这个数.
2.有理数的减法
减法法则:
减去一个数,等于加上这个数的相反数.
3.有理数的乘法
(1)乘法法则
异号两数相乘得负数,并且把绝对值相乘.
任何数与0相乘,仍得0.
同号两数相乘得正数,并且把绝对值相乘.
(2)几个不等于0的数相乘,当负因数有奇数个时,积为负;当负因数有偶数个时,积为正.
(2)同号两数相除得正数,异号两数相除得负数,并把它们的绝对值相除;0除以任何一个不等于0的数都得0.
4.有理数的除法
(3)乘法的运算律
(3)除以一个不为0的数,等于乘以这个数的倒数.
乘法交换律:
乘法结合律
乘法的分配律
(1)对于两个有理数a,b,其中b≠0,如果有一个有理数c,使得cb=a,那么规定a÷b=c,且把c叫做a除以b的商.
5.有理数的乘方
(1)求n个相同因数的积的运算,叫做乘方.乘方的结果叫做幂.在an中,a叫做底数,n叫做指数.
幂
指数
底数
(2)正数的任何正整数次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0的任何正整数次幂都是0.
特别地,a2通常读作a的平方,a3通常读作a的立方.
a1规定为a.
(1)先算乘方,再算乘除,最后算加减;
(2)同级运算,从左到右进行;
(3)如有括号,先进行括号里面的运算,按小括号、中括号、大括号依次进行.
6.有理数的混合运算
四、科学记数法
(2)n为原数的整数位减去1.
(1)把一个绝对值大于10的数记做 a×10n的形式,其中a是整数数位只有一位的数(即1≤|a|<10),这种记数法叫做科学记数法.
注意
考 点 讲 练
考点一 正、负数的意义
例1 如果-4米表示向东走4米,那么向西走2米记作_____.
+2米
【解析】根据题意,可知向东记为负,向西记为正, 故向西走2米记做+2米.
【方法总结】根据相反意义合理使用正、负数对实际问题进行表示.一般情况下,把向北(东)、上升、增加、收入等规定为正,把它们的相反意义规定为负.
注意带单位
针对训练
1.下列语句中,含有相反意义的两个量是( )
A.盈利1千元和收入2千元
B.上升8米和后退8米
C.存入1千元和取出2千元
D.超过2厘米和上涨2厘米
C
-8
2.上升9记作+9,那么下降8记作____.
考点二 正、负数的概念
例2 判断:
①不带“-”号的数都是正数 ( )
④一个有理数不是正数就是负数 ( )
⑤ 0℃表示没有温度 ( )
②如果a是正数,那么-a一定是负数( )
③不存在既不是正数,也不是负数的数( )
×
×
×
×
√
【解析】①0不带“-”号,但0不是正数,故①错误;②正数的相反数是负数,故②正确;③同①,故③错误;④同③,故④错误;⑤0℃并不是表示没有温度,它是介于正温度与负温度之间,故⑤错误.
方法总结
0既不是正数也不是负数,0的相反数是它本身.
0不仅能表示没有,而且表示正、负之间的分界值.
考点三 有理数的分类
例3 将下列各数分别填入下列相应的圈内:
3.5
|-2|
0
-3.5
-2
-1
3
5
-
1
3
0.5
, , , , , , ,
正数
负数
整数
分数
3.5,
|-2|,
0.5
-3.5
,-2
,-1
3
5
,-
1
3
0
,|-2|
,-2
3.5,
,0.5
-3.5,
-1
3
5
,-
1
3
针对训练
【解析】负分数不仅是负数而且是分数,注意小数也属于分数.故只有2个.
2
3.在+3.5,0,11,-2, ,-0.7 中,负分数有 个.
考点四 相反数、倒数、绝对值
例4 填表
3.5
|-2|
0
-3.5
-2
-1
3
5
-
1
3
0.5
数
相反数
倒数
绝对值
-3.5
-2
0
3.5
2
-0.5
1
3
5
1
3
3.5
2
0
3.5
2
0.5
1
3
5
1
3
-3
没有
-0.5
2
0.5
-
2
7
2
7
-
5
8
1
1
3
-3
–5的绝对值是 .
5
针对训练
4. 的倒数是 ; 的相反数是 ;
-
1
3
考点五 数轴
例5 请你将下面的数在数轴上表示出来
3.5
|-2|
0
-3.5
-2
0.5
, , , , , , ,
-1
3
5
-
1
3
解:表示如下
针对训练
5.在数轴上,点A所表示的数为2,那么到点A的距离等于3个单位长度的点所表示的数是________.
-1或3
考点六 有理数比较大小
例6 请你将下面的数用“>”连接起来
解法一:将各数在数轴上表示出来,右边的大于左边的,然后从大到小排列
解法二:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小.
6.某日零点,北京、上海、宁夏的气温分别是﹣4℃、5℃、6℃、﹣8℃,当时这四个城市中,气温最低的是 ( )
A.北京 B.上海 C.重庆 D.宁夏
针对训练
D
考点七 科学记数法
例7 将数13 445 000 000 000km用科学记数法表示___________m.
1.3445×1016
注意统一单位
7.2016年末上海市常住人口总数为2615.27万人,用科学记数法表示为 人.
2.61527×107
针对训练
考点八 有理数的运算
例8 计算
(1)
(2)
(3)
(4)
1.把减法转化为加法时,要注意符号.
2.对几个有理数相加减的题目,要注意观察,将哪些数放在一起会使计算简便
解:(1)
(2)
注意符号问题
(3)
先确定商的符号,再把绝对值相除
注意:1.底数是带分数时,要先将带分数化成假分数.
2.区分-24与(-2)4.
(4)
针对训练
9.计算
(1)
(2)
(3)
(4)
答案:(1)-17
(2)33
(3)-3.3
课 堂 小 结
整数
分数
负分数
正分数
正有理数
负有理数
0
有理数
0
正整数
负整数
有
理
数
数轴
比较大小
相反数
点与数的对应
绝对值
倒数
科学记数法
有理数运算
减法
加法
乘法
乘方
除法
交换律、结合律
法则
运算律
转 化
加法
乘法
混
合
运
算
按
顺
序
进
行
转 化
交换律、结合律、分配律
thanks for your coming
同课章节目录
