第二章整式的加减复习课
图片预览






文档简介
课件18张PPT。谢谢倾听
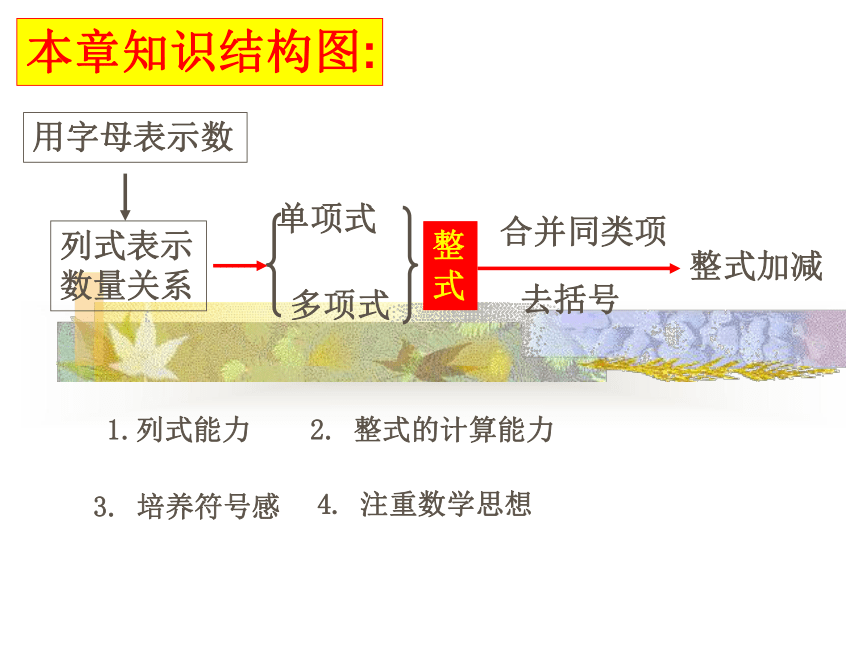
敬请指导祝同学们学习愉快!!!第二章整式的加减整式的加减复习课用字母表示数列式表示数量关系单项式多项式整式整式加减合并同类项去括号本章知识结构图:1.列式能力2. 整式的计算能力3. 培养符号感4. 注重数学思想列代数式应该注意四点: (1)代数式中出现乘号,通常写作“."或者省略不写. (2)数字与字母相乘时,数字写在字母前面. (3)除法运算写成分数形式. (4)当表示和或差而后面有单位时,代数式应加括号. (1)圆周率?是常数。(2)如果单项式是单独的字母,那么它的系数是1。如:单项式c的系数是1。(3)当一个单项式的系数是1或–1时,“1” 通常省略不写,但不要误认为是0,如a2,–abc;(4)单项式的系数是带分数时,还常写成假分数,如 写成 。(5)单独的数字不含字母,所以它的次数是零次.注意:注意以上代数式中,哪些符合书写要求?×××××√(1)单项式是由数与字母的乘积组成的代数式;
单独的一个数或字母也是单项式;
单项式的数字因数叫做单项式的系数;
单项式中所有字母的指数的和叫做单项式的次数,而且次数只与字母有关。关于整式的概念(2)多项式是建立在单项式概念基础上,几个单项式的和就是多项式;
每个单项式是该多项式的一个项;每项包括它前面的符号,这点一定要注意。
组成多项式的每个单项式的次数是该多项式各项的次数;“几次项”中“次”就是指这个次数;
多项式的次数,是指示最高次项发次数。(3) 单项式和多项式是统称为整式。1、下列各式中哪些是单项式(系数、次数),哪些是多项式(项、次数)?关于同类项和合并同类项1、对于同类项应从概念出发,掌握判断标准:
(1)字母相同;
(2)相同字母的指数相同;
(3)与系数无关;
(4)与字母的顺序无关。 2、合并同类项是整式加减的基础。法则:合并同类项,只把系数相加减,字母及字母的指数不变。
注意以下几点:(前提:正确判断同类项)
(1)常数项是同类项,所以几个常数项可以合并;
(2)两个同类项系数互为相反数,则这两项的和等于0;
(3)同类项中的“合并”是指同类项系数求和,把所得到结果作为新的项的系数,字母与字母的指数不变。
(4)只有同类项才能合并,不是同类项就不能合并。 两相同两无关练习:1、若 与 是同类项,则m= ,n= 。 2、 下列各题计算的结果对不对?如果不对,指出错在哪里?××××√1761、去括号是本章的难点之一;去括号都是多项式的恒等变形;去括号时一定对照法则把去掉括号与括号的符号看成统一体,不能拆开。
法则:如果括号外的因数是正数,去括号后原括号内的各项的符号与原来的符号( );
如果括号外的因数是负数,去括号后原括号内的各项的符号与原来的符号( )。
遇到括号前面是“-”时,容易发生漏掉括号内一部分项的变号,所以,要注意“各项”都要变号。不是只变第一项的符号。
去括号的顺口溜:去括号,看符号;
是正号,不变号;
是负号,全变号。关于去括号相同相反基础练习2ab2-8x3xa+b-c-da-b+c-d12x-6-5+x12a -12b4x+3所含______相同,并且__________的指数也相同的项叫做同类项。字母相同的字母把多项式中的_______合并成一项,叫做合并同类项。 同类项负变正不变,要变全都变 整式加减的法则:有括号就先________,然后再__________。去括号合并同类项思考:已知A=3x+2,B=x-5,求(1)A+B?;(2)3A-2B.解:由已知得:
(1)A+B
=(3x+2)+(x-5)
=3x+2+x-5
=4x-3;(2)3A-2B
=3(3x+2)-2(x-5)
= (9x+6)- (2x-10)
=9x+6-2x+10
=7x+16.分析:被减式=减式+差
(3x2 -6x+5)+(4x2+7x -6)已知某多项式与3x2-6x+5的差是 4x 2+7x - 6,求此多项式. 若两个单项式的和是:2x2+xy+3y2,一个加式是x2-xy,求另一个加式.课堂练习1.选择题:
(1)一个二次式加上一个一次式,其和是( )
A.一次式 B.二次式 C.三次式 D.次数不定
(2).一个二次式加上一个二次式,其和是( )
A.一次式 B.二次式
C.常数 D. 次式不高于二次的整式
(3). 一个二次式减去一个一次式,其差是( )
A.一次式 B.二次式 C.常数 D. 次数不定练一练BDB如图,摆n个这样联体图形需 根火柴棒。(3n+1)2、联体长方形的摆法:(填空)3.十位数字是m,个位数字比m小3,百位数字是m的3倍,这个三位数是 . 祝同学们学习愉快!!!
敬请指导祝同学们学习愉快!!!第二章整式的加减整式的加减复习课用字母表示数列式表示数量关系单项式多项式整式整式加减合并同类项去括号本章知识结构图:1.列式能力2. 整式的计算能力3. 培养符号感4. 注重数学思想列代数式应该注意四点: (1)代数式中出现乘号,通常写作“."或者省略不写. (2)数字与字母相乘时,数字写在字母前面. (3)除法运算写成分数形式. (4)当表示和或差而后面有单位时,代数式应加括号. (1)圆周率?是常数。(2)如果单项式是单独的字母,那么它的系数是1。如:单项式c的系数是1。(3)当一个单项式的系数是1或–1时,“1” 通常省略不写,但不要误认为是0,如a2,–abc;(4)单项式的系数是带分数时,还常写成假分数,如 写成 。(5)单独的数字不含字母,所以它的次数是零次.注意:注意以上代数式中,哪些符合书写要求?×××××√(1)单项式是由数与字母的乘积组成的代数式;
单独的一个数或字母也是单项式;
单项式的数字因数叫做单项式的系数;
单项式中所有字母的指数的和叫做单项式的次数,而且次数只与字母有关。关于整式的概念(2)多项式是建立在单项式概念基础上,几个单项式的和就是多项式;
每个单项式是该多项式的一个项;每项包括它前面的符号,这点一定要注意。
组成多项式的每个单项式的次数是该多项式各项的次数;“几次项”中“次”就是指这个次数;
多项式的次数,是指示最高次项发次数。(3) 单项式和多项式是统称为整式。1、下列各式中哪些是单项式(系数、次数),哪些是多项式(项、次数)?关于同类项和合并同类项1、对于同类项应从概念出发,掌握判断标准:
(1)字母相同;
(2)相同字母的指数相同;
(3)与系数无关;
(4)与字母的顺序无关。 2、合并同类项是整式加减的基础。法则:合并同类项,只把系数相加减,字母及字母的指数不变。
注意以下几点:(前提:正确判断同类项)
(1)常数项是同类项,所以几个常数项可以合并;
(2)两个同类项系数互为相反数,则这两项的和等于0;
(3)同类项中的“合并”是指同类项系数求和,把所得到结果作为新的项的系数,字母与字母的指数不变。
(4)只有同类项才能合并,不是同类项就不能合并。 两相同两无关练习:1、若 与 是同类项,则m= ,n= 。 2、 下列各题计算的结果对不对?如果不对,指出错在哪里?××××√1761、去括号是本章的难点之一;去括号都是多项式的恒等变形;去括号时一定对照法则把去掉括号与括号的符号看成统一体,不能拆开。
法则:如果括号外的因数是正数,去括号后原括号内的各项的符号与原来的符号( );
如果括号外的因数是负数,去括号后原括号内的各项的符号与原来的符号( )。
遇到括号前面是“-”时,容易发生漏掉括号内一部分项的变号,所以,要注意“各项”都要变号。不是只变第一项的符号。
去括号的顺口溜:去括号,看符号;
是正号,不变号;
是负号,全变号。关于去括号相同相反基础练习2ab2-8x3xa+b-c-da-b+c-d12x-6-5+x12a -12b4x+3所含______相同,并且__________的指数也相同的项叫做同类项。字母相同的字母把多项式中的_______合并成一项,叫做合并同类项。 同类项负变正不变,要变全都变 整式加减的法则:有括号就先________,然后再__________。去括号合并同类项思考:已知A=3x+2,B=x-5,求(1)A+B?;(2)3A-2B.解:由已知得:
(1)A+B
=(3x+2)+(x-5)
=3x+2+x-5
=4x-3;(2)3A-2B
=3(3x+2)-2(x-5)
= (9x+6)- (2x-10)
=9x+6-2x+10
=7x+16.分析:被减式=减式+差
(3x2 -6x+5)+(4x2+7x -6)已知某多项式与3x2-6x+5的差是 4x 2+7x - 6,求此多项式. 若两个单项式的和是:2x2+xy+3y2,一个加式是x2-xy,求另一个加式.课堂练习1.选择题:
(1)一个二次式加上一个一次式,其和是( )
A.一次式 B.二次式 C.三次式 D.次数不定
(2).一个二次式加上一个二次式,其和是( )
A.一次式 B.二次式
C.常数 D. 次式不高于二次的整式
(3). 一个二次式减去一个一次式,其差是( )
A.一次式 B.二次式 C.常数 D. 次数不定练一练BDB如图,摆n个这样联体图形需 根火柴棒。(3n+1)2、联体长方形的摆法:(填空)3.十位数字是m,个位数字比m小3,百位数字是m的3倍,这个三位数是 . 祝同学们学习愉快!!!
