分式的运算复习课[下学期]
文档属性
| 名称 | 分式的运算复习课[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 230.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-14 00:00:00 | ||
图片预览







文档简介
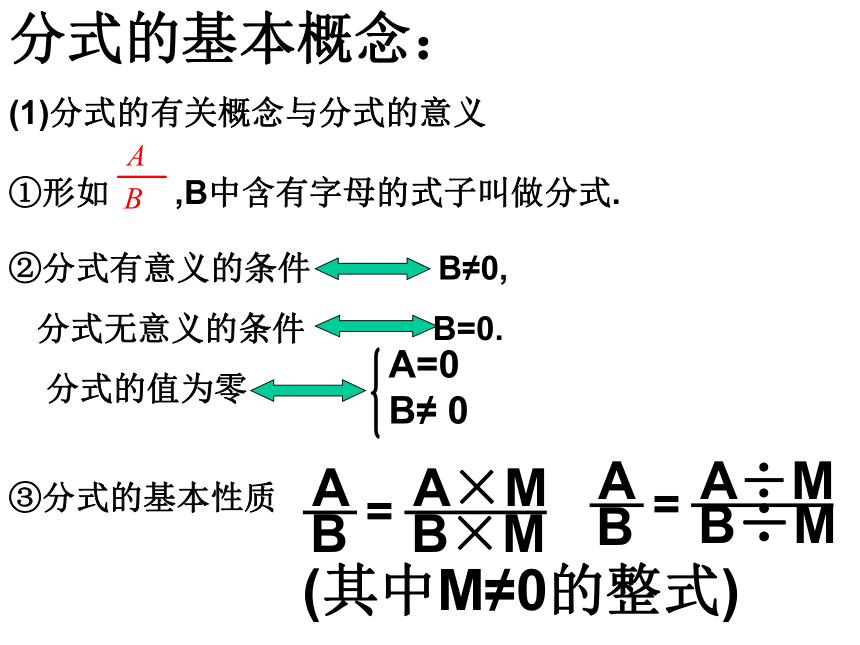
课件21张PPT。分式和分式方程 复习(其中M≠0的整式)(1)分式的有关概念与分式的意义
①形如 ,B中含有字母的式子叫做分式.分式的基本概念:②分式有意义的条件 B≠0,
分式无意义的条件 B=0.
分式的值为零③分式的基本性质(2)分式乘除法
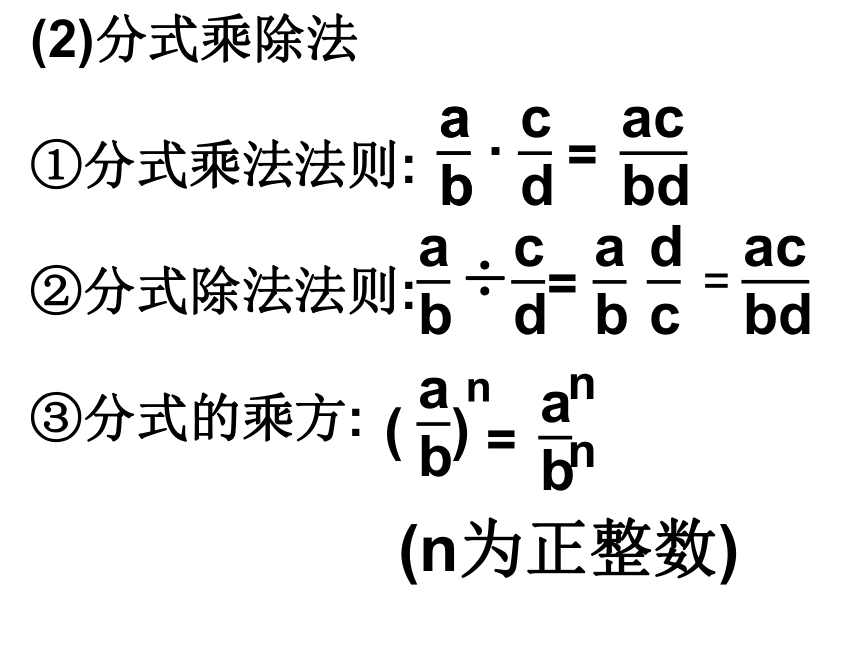
①分式乘法法则:
②分式除法法则:
③分式的乘方:÷=acbd=( )n=nn(n为正整数)(3)分式的运算:
①约分:把一个分式的分子分母中公因式约去(即分子分母同时除以它们的公因式)叫做分式的约分.分子分母中没有公因式时叫做最简分式.②分式的通分把几个异分母的分式化为与原来的分式相等的同分母的分式叫做分式的通分。③同分母分式相加减的法则④异分母分式相加减的法则.(4).零指数幂与负指数幂
a×10n (其中1≤|a|<10,n为整数)(1)零指数幂:a0=1 (a≠ 0)
am÷am=am-m=1 (a≠ 0) (3)科学记数法表示绝对值较大数和绝对值较小的数.写成形如:D基本入关练习C.____,____;,.=---=-xxxxxxx则的值为若分式则无意义若分式0221223. 不改变分式的值,将分式的分子、分母各项的系数化为整数,并使分子、分母的首项系数为正4.下列各式的恒等变形是否正确?为什么?(5)约分:(6)通分:当分子或分母为多项式时,可以先对它们进行因式分解.分式的三大基本内容:1.分式的基本概念;2.分式的基本性质;3.分式的基本运算;重难专攻.综合方法例题3 计算:=2点评:1.注意符号的变化
2.通过约分也能达到通分的目的练习点评:在化简中要有整体思想意识,运用技巧。 要注意分式中的隐含条件,分母不为0是分式学习的要点剑指提高用简便方法计算:大显身手重击2.归纳猜想题(1)观察下列各式:112=13×4=-,,,…,由此可推测:(2)请猜想出能表示出(1)的特点的一般
规律,用含字母n的等式表示出来(n为
正整数),并证明.(3)请用(2)中的规律计算:
,4.已知两个分式A= ,B=4x2-41x+2+12-x下面有三个结论(1)A=B(2)A,B互为相
反数(3)A,B互为倒数.请问哪个正确?5.有这样一道题:计算x2-2x+1x2-1÷x-1x2+x-x的值,其中x=2004,甲同学把x=2004
错抄成x=2040,但他的计算结果也是
正确的,你说这是怎么回事?6.已知P=Q=(x+y)2 -2y(x+y)小敏,小聪两人在x=2,y=-1的条件下
分别计算了P和Q的值,小敏说P的值
比Q大,小聪说Q的值比P大,请你判断
谁的结论正确,并说明理由.练习
①形如 ,B中含有字母的式子叫做分式.分式的基本概念:②分式有意义的条件 B≠0,
分式无意义的条件 B=0.
分式的值为零③分式的基本性质(2)分式乘除法
①分式乘法法则:
②分式除法法则:
③分式的乘方:÷=acbd=( )n=nn(n为正整数)(3)分式的运算:
①约分:把一个分式的分子分母中公因式约去(即分子分母同时除以它们的公因式)叫做分式的约分.分子分母中没有公因式时叫做最简分式.②分式的通分把几个异分母的分式化为与原来的分式相等的同分母的分式叫做分式的通分。③同分母分式相加减的法则④异分母分式相加减的法则.(4).零指数幂与负指数幂
a×10n (其中1≤|a|<10,n为整数)(1)零指数幂:a0=1 (a≠ 0)
am÷am=am-m=1 (a≠ 0) (3)科学记数法表示绝对值较大数和绝对值较小的数.写成形如:D基本入关练习C.____,____;,.=---=-xxxxxxx则的值为若分式则无意义若分式0221223. 不改变分式的值,将分式的分子、分母各项的系数化为整数,并使分子、分母的首项系数为正4.下列各式的恒等变形是否正确?为什么?(5)约分:(6)通分:当分子或分母为多项式时,可以先对它们进行因式分解.分式的三大基本内容:1.分式的基本概念;2.分式的基本性质;3.分式的基本运算;重难专攻.综合方法例题3 计算:=2点评:1.注意符号的变化
2.通过约分也能达到通分的目的练习点评:在化简中要有整体思想意识,运用技巧。 要注意分式中的隐含条件,分母不为0是分式学习的要点剑指提高用简便方法计算:大显身手重击2.归纳猜想题(1)观察下列各式:112=13×4=-,,,…,由此可推测:(2)请猜想出能表示出(1)的特点的一般
规律,用含字母n的等式表示出来(n为
正整数),并证明.(3)请用(2)中的规律计算:
,4.已知两个分式A= ,B=4x2-41x+2+12-x下面有三个结论(1)A=B(2)A,B互为相
反数(3)A,B互为倒数.请问哪个正确?5.有这样一道题:计算x2-2x+1x2-1÷x-1x2+x-x的值,其中x=2004,甲同学把x=2004
错抄成x=2040,但他的计算结果也是
正确的,你说这是怎么回事?6.已知P=Q=(x+y)2 -2y(x+y)小敏,小聪两人在x=2,y=-1的条件下
分别计算了P和Q的值,小敏说P的值
比Q大,小聪说Q的值比P大,请你判断
谁的结论正确,并说明理由.练习
