椭圆的定义及其标准方程
图片预览






文档简介
课件25张PPT。椭圆及其标准方程一.课题引入:生活中的椭圆自然界处处存在着椭圆,那么如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢?或者说椭圆是什么样点的轨迹呢?想一想复习:圆的定义平面内到一定点的距离等于定长的点的轨迹.
思考:平面内到两定点距离之和等于定长的点的轨迹又是什么呢? 取一条定长的细绳,把它的两端用图钉固定在黑板上的F1和F2两点,用笔尖拉紧绳,使笔尖在画板上慢慢地移动,观察画出的轨迹是什么图形。
反 思动手实验(1)在画出一个椭圆的过程中, 图钉F1和F2两点的位置是固定的还是运动的?
(2)在画椭圆的过程中,绳子的长度变了没有?说明了什么?
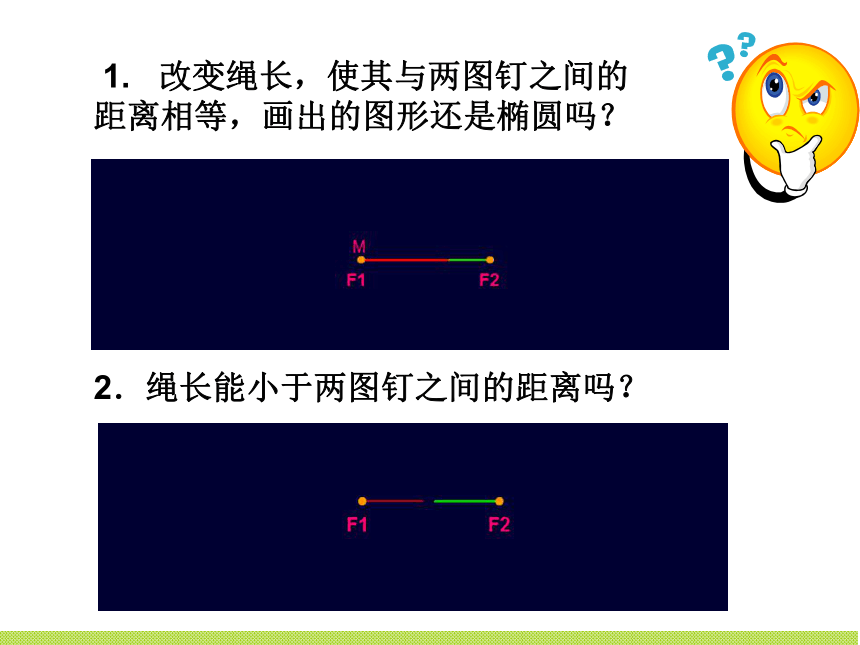
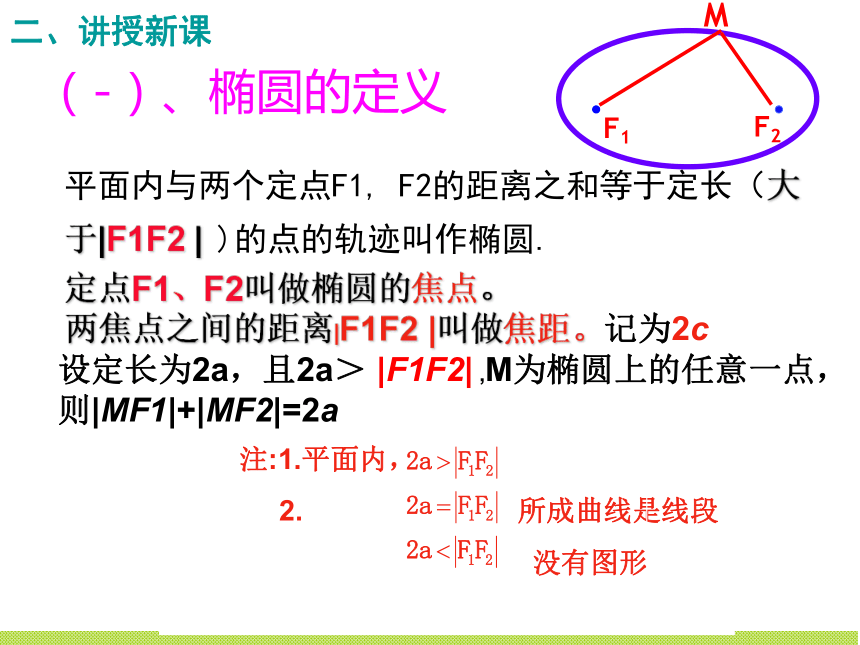
(3)在画椭圆的过程中,绳子长度与两定点距离大小有怎样的关系? 1. 改变绳长,使其与两图钉之间的距离相等,画出的图形还是椭圆吗?2.绳长能小于两图钉之间的距离吗? 1. 改变绳长,使其与两图钉之间的距离相等,画出的图形还是椭圆吗?2.绳长能小于两图钉之间的距离吗? 平面内与两个定点F1, F2的距离之和等于定长(大于|F1F2 | )的点的轨迹叫作椭圆. (-)、椭圆的定义定点F1、F2叫做椭圆的焦点。
两焦点之间的距离|F1F2 |叫做焦距。记为2c设定长为2a,且2a> |F1F2| ,M为椭圆上的任意一点,则|MF1|+|MF2|=2a
二、讲授新课求曲线方程的基本步骤?1:建系
2:设点
3:找等量关系
4:代入坐标
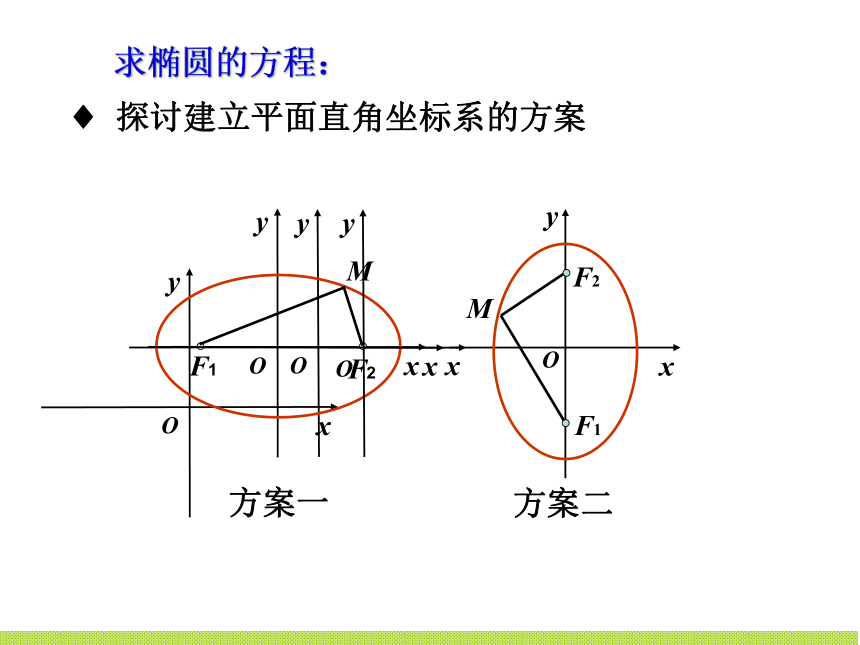
5:化简,检验(二)、椭圆的标准方程? 探讨建立平面直角坐标系的方案方案一求椭圆的方程:解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图). 则有F1(-c,0), F2(c,0)
设M(x, y)是椭圆上任意一点(问题:下面怎样化简?)由椭圆的定义得:代入坐标两边除以 得由椭圆定义可知整理得两边再平方,得移项,平方椭圆的标准方程(一)(a>b>0)它表示椭圆的几何特征;
1:焦点在x轴上
2:焦点坐标为F1(-c,0), F2(c,0)
3:椭圆的标准方程(二)(a>b>0)它表示椭圆的几何特征;
1:焦点在y轴上
2:焦点坐标为F1(0,-c),F2(0,c)
3:总体印象:对称、简洁,“像”直线方程的截距式 椭圆的标准方程如何确定焦点的位置?看 分母大小,哪个分母大就在哪一条轴上 谁大在谁上则a= ,b= 焦点在则a= ,b= 焦点在 轴上;53则a= ,b= ;焦点在 轴上。3 轴上;XX快速反应巩固性练习题组一方法总结:判断焦点位置------化方程为标准式,谁大在谁上。 Y或巩固性练习题组二例1、求满足下列条件的椭圆的标准方程:(1)两焦点的坐标分别是(-4,0)、(4,0),
椭圆上一点P到两焦点距离之和等于10。(2)两焦点的坐标分别是(-2,0)、(2,0),
且椭圆经过点P 。(2)两焦点的坐标分别是(-2,0)、(2,0),且
椭圆经过点P 。解:因为椭圆的焦点在X轴上,所以可设它的方程为:?由椭圆的定义可知:又因 c=2,所以椭圆的标准方程为:故 b2=a2-c2=10-22=6又解: 设所求的标准方程为 所以所求椭圆的标准方程为:.解法2 (3) 焦点在坐标轴上,并且经过两点
A(0, 2),B , 方法总结:
如何根据已知条件求椭圆的标准方程:待定系数法(1)定类型----确定焦点位置;(2)设方程---设出满足题意的标准方程;(3)求系数----求解a,b的值,写出标准方程。注:当焦点位置不确定时,要讨论。当椭圆过两定
点时,设方程为:
(1)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则△F2CD的周长为________543(3,0)、(-3,0)620巩固性练习题组三(2)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:___________焦距等于__________;曲线上一点P到焦点F1的距离为3,则点P到另一个焦点F2的距离等于_________,则△F1PF2的周长为___________21(0,-1)、(0,1)2课堂小结:本节课我们学习了
1.一个定义
2.两个方程
3.三个基本量a, b, c. 课后作业:成才之路P13:
1~4,7~12,15,16
反 思动手实验(1)在画出一个椭圆的过程中, 图钉F1和F2两点的位置是固定的还是运动的?
(2)在画椭圆的过程中,绳子的长度变了没有?说明了什么?
(3)在画椭圆的过程中,绳子长度与两定点距离大小有怎样的关系? 1. 改变绳长,使其与两图钉之间的距离相等,画出的图形还是椭圆吗?2.绳长能小于两图钉之间的距离吗? 1. 改变绳长,使其与两图钉之间的距离相等,画出的图形还是椭圆吗?2.绳长能小于两图钉之间的距离吗? 平面内与两个定点F1, F2的距离之和等于定长(大于|F1F2 | )的点的轨迹叫作椭圆. (-)、椭圆的定义定点F1、F2叫做椭圆的焦点。
两焦点之间的距离|F1F2 |叫做焦距。记为2c设定长为2a,且2a> |F1F2| ,M为椭圆上的任意一点,则|MF1|+|MF2|=2a
二、讲授新课求曲线方程的基本步骤?1:建系
2:设点
3:找等量关系
4:代入坐标
5:化简,检验(二)、椭圆的标准方程? 探讨建立平面直角坐标系的方案方案一求椭圆的方程:解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图). 则有F1(-c,0), F2(c,0)
设M(x, y)是椭圆上任意一点(问题:下面怎样化简?)由椭圆的定义得:代入坐标两边除以 得由椭圆定义可知整理得两边再平方,得移项,平方椭圆的标准方程(一)(a>b>0)它表示椭圆的几何特征;
1:焦点在x轴上
2:焦点坐标为F1(-c,0), F2(c,0)
3:椭圆的标准方程(二)(a>b>0)它表示椭圆的几何特征;
1:焦点在y轴上
2:焦点坐标为F1(0,-c),F2(0,c)
3:总体印象:对称、简洁,“像”直线方程的截距式 椭圆的标准方程如何确定焦点的位置?看 分母大小,哪个分母大就在哪一条轴上 谁大在谁上则a= ,b= 焦点在则a= ,b= 焦点在 轴上;53则a= ,b= ;焦点在 轴上。3 轴上;XX快速反应巩固性练习题组一方法总结:判断焦点位置------化方程为标准式,谁大在谁上。 Y或巩固性练习题组二例1、求满足下列条件的椭圆的标准方程:(1)两焦点的坐标分别是(-4,0)、(4,0),
椭圆上一点P到两焦点距离之和等于10。(2)两焦点的坐标分别是(-2,0)、(2,0),
且椭圆经过点P 。(2)两焦点的坐标分别是(-2,0)、(2,0),且
椭圆经过点P 。解:因为椭圆的焦点在X轴上,所以可设它的方程为:?由椭圆的定义可知:又因 c=2,所以椭圆的标准方程为:故 b2=a2-c2=10-22=6又解: 设所求的标准方程为 所以所求椭圆的标准方程为:.解法2 (3) 焦点在坐标轴上,并且经过两点
A(0, 2),B , 方法总结:
如何根据已知条件求椭圆的标准方程:待定系数法(1)定类型----确定焦点位置;(2)设方程---设出满足题意的标准方程;(3)求系数----求解a,b的值,写出标准方程。注:当焦点位置不确定时,要讨论。当椭圆过两定
点时,设方程为:
(1)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则△F2CD的周长为________543(3,0)、(-3,0)620巩固性练习题组三(2)已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:___________焦距等于__________;曲线上一点P到焦点F1的距离为3,则点P到另一个焦点F2的距离等于_________,则△F1PF2的周长为___________21(0,-1)、(0,1)2课堂小结:本节课我们学习了
1.一个定义
2.两个方程
3.三个基本量a, b, c. 课后作业:成才之路P13:
1~4,7~12,15,16
