分式方程[下学期]
图片预览

文档简介
§16.3 分式方程复习题
1、下列方程中是分式方程的是 ( )
A、 B、 C、 D、
2、解分式方程,去分母后所得的方程是 ( )
A、1-3(2x+1)=3 B、1-3(2x+1)=3x C、1-6x+3=9x D 、1-3(2x+1)=9x
3、化分式方程为整式方程时,方程两边须同乘以( )
A、(5x2-5)(x2-1)(1-x) B、5(x2-1)(1-x) C、5(x2-1)(x-1) D、5(x+1)(x-1)
4、下列说法中错误的是 ( )
A、分式方程的解等于0,就说明这个分式方程无解.
B、解分式方程的基本思路是把分式方程转化为整式方程.
C、检验是解分式方程必不可少的步骤.
D、能使分式方程的最简公分母等于零的未知数的值不是原分式方程的解.
5、 下列结论中,不正确的是 ( )
A、方程的解是x=2 B、方程的解是x=-5
C、方程的解是x=2 D、方程的解是x=3
6、关于x的方程的解是x=3,则a的值为________.
7、若与互为相反数,则可得方程______________,解得x=_______.
8、若关于x的方程无解,则m的值为________.
9、如图,△ABC是等边三角形,表示其边长的代数式均 2x-8 3y+2
已在图中标出,则代数式的值为_________ . x+6
10、某企业计划建立职工图书室,本月打算新添某种图书x本,若用60元去购买就多买5本,若用40元去买就少5本,则下列方程正确的是( )
A、 B、 C、 D、
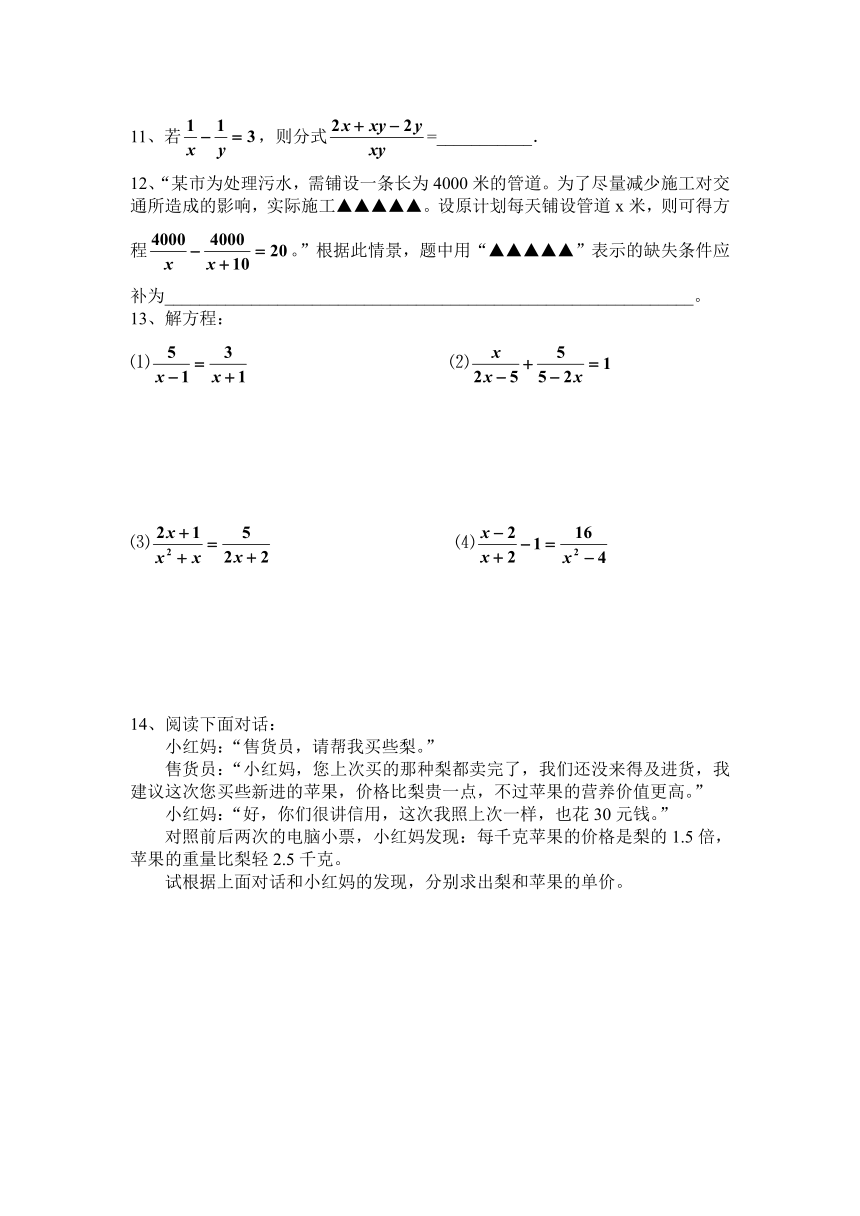
11、若,则分式=___________.
12、“某市为处理污水,需铺设一条长为4000米的管道。为了尽量减少施工对交通所造成的影响,实际施工▲▲▲▲▲。设原计划每天铺设管道x米,则可得方程。”根据此情景,题中用“▲▲▲▲▲”表示的缺失条件应补为_____________________________________________________________。
13、解方程:
⑴ ⑵
⑶ ⑷
14、阅读下面对话:
小红妈:“售货员,请帮我买些梨。”
售货员:“小红妈,您上次买的那种梨都卖完了,我们还没来得及进货,我建议这次您买些新进的苹果,价格比梨贵一点,不过苹果的营养价值更高。”
小红妈:“好,你们很讲信用,这次我照上次一样,也花30元钱。”
对照前后两次的电脑小票,小红妈发现:每千克苹果的价格是梨的1.5倍,苹果的重量比梨轻2.5千克。
试根据上面对话和小红妈的发现,分别求出梨和苹果的单价。
练习
1、下列方程不是分式方程的是 ( )
A、 B、 C、 D、
2、解分式方程,下列说法错误的是 ( )
A、方程两边分式的最简公分母是(x+1)(x-1).
B、方程两边乘以(x+1)(x-1),得整式方程2(x-1)+3(x+1)=6.
C、解这个整式方程(指B中),得x=1.
D、原分式方程的解为x=1.
3、方程的解的情况为 ( )
A、x=3 B、x=-3 C、无解 D、解为除-3以外的任意数
4、下列结论中正确的是 ( )
A、方程的解是x=2 B、方程的解是x=5
C、方程的解是x=4 D、方程的解是x=3
5、一组学生去郊游,预计共需费用120元,后来又有2个人参加进来,总费用不变,于是每人可少分摊3元。若设原来这组学生有x人,则可列方程为( )
A、 B、
C、 D、
6、当x_______时,的值等于.
7、当x_______时,的值与的值相等.
8、若方程的解是最小的正整数,则a的值为__________.
9、若关于x的方程无解,则m=_________.
10、若,则分式的值为____________.
11、某化肥厂原计划每天生产化肥x吨,由于采取了新技术,每天多生产化肥3吨,实际生产180吨与原计划生产120吨的时间相等。则可列出x的方程为_______________________.
12、解方程:
⑴ ⑵ ⑶
⑷ ⑸
13、小明和小芳同时从张庄出发,步行15千米到李庄,小芳步行的速度是小明步行速度的1.2倍,结果比小明早到半小时。
⑴设小明每小时走x千米,请根据题意填写下表:
每小时走的路程(千米) 走完全程所用的时间(小时)
小明 x
小芳
⑵根据题意及表中所得到的信息列方程,求二人每小时各走几千米?
1、下列方程中是分式方程的是 ( )
A、 B、 C、 D、
2、解分式方程,去分母后所得的方程是 ( )
A、1-3(2x+1)=3 B、1-3(2x+1)=3x C、1-6x+3=9x D 、1-3(2x+1)=9x
3、化分式方程为整式方程时,方程两边须同乘以( )
A、(5x2-5)(x2-1)(1-x) B、5(x2-1)(1-x) C、5(x2-1)(x-1) D、5(x+1)(x-1)
4、下列说法中错误的是 ( )
A、分式方程的解等于0,就说明这个分式方程无解.
B、解分式方程的基本思路是把分式方程转化为整式方程.
C、检验是解分式方程必不可少的步骤.
D、能使分式方程的最简公分母等于零的未知数的值不是原分式方程的解.
5、 下列结论中,不正确的是 ( )
A、方程的解是x=2 B、方程的解是x=-5
C、方程的解是x=2 D、方程的解是x=3
6、关于x的方程的解是x=3,则a的值为________.
7、若与互为相反数,则可得方程______________,解得x=_______.
8、若关于x的方程无解,则m的值为________.
9、如图,△ABC是等边三角形,表示其边长的代数式均 2x-8 3y+2
已在图中标出,则代数式的值为_________ . x+6
10、某企业计划建立职工图书室,本月打算新添某种图书x本,若用60元去购买就多买5本,若用40元去买就少5本,则下列方程正确的是( )
A、 B、 C、 D、
11、若,则分式=___________.
12、“某市为处理污水,需铺设一条长为4000米的管道。为了尽量减少施工对交通所造成的影响,实际施工▲▲▲▲▲。设原计划每天铺设管道x米,则可得方程。”根据此情景,题中用“▲▲▲▲▲”表示的缺失条件应补为_____________________________________________________________。
13、解方程:
⑴ ⑵
⑶ ⑷
14、阅读下面对话:
小红妈:“售货员,请帮我买些梨。”
售货员:“小红妈,您上次买的那种梨都卖完了,我们还没来得及进货,我建议这次您买些新进的苹果,价格比梨贵一点,不过苹果的营养价值更高。”
小红妈:“好,你们很讲信用,这次我照上次一样,也花30元钱。”
对照前后两次的电脑小票,小红妈发现:每千克苹果的价格是梨的1.5倍,苹果的重量比梨轻2.5千克。
试根据上面对话和小红妈的发现,分别求出梨和苹果的单价。
练习
1、下列方程不是分式方程的是 ( )
A、 B、 C、 D、
2、解分式方程,下列说法错误的是 ( )
A、方程两边分式的最简公分母是(x+1)(x-1).
B、方程两边乘以(x+1)(x-1),得整式方程2(x-1)+3(x+1)=6.
C、解这个整式方程(指B中),得x=1.
D、原分式方程的解为x=1.
3、方程的解的情况为 ( )
A、x=3 B、x=-3 C、无解 D、解为除-3以外的任意数
4、下列结论中正确的是 ( )
A、方程的解是x=2 B、方程的解是x=5
C、方程的解是x=4 D、方程的解是x=3
5、一组学生去郊游,预计共需费用120元,后来又有2个人参加进来,总费用不变,于是每人可少分摊3元。若设原来这组学生有x人,则可列方程为( )
A、 B、
C、 D、
6、当x_______时,的值等于.
7、当x_______时,的值与的值相等.
8、若方程的解是最小的正整数,则a的值为__________.
9、若关于x的方程无解,则m=_________.
10、若,则分式的值为____________.
11、某化肥厂原计划每天生产化肥x吨,由于采取了新技术,每天多生产化肥3吨,实际生产180吨与原计划生产120吨的时间相等。则可列出x的方程为_______________________.
12、解方程:
⑴ ⑵ ⑶
⑷ ⑸
13、小明和小芳同时从张庄出发,步行15千米到李庄,小芳步行的速度是小明步行速度的1.2倍,结果比小明早到半小时。
⑴设小明每小时走x千米,请根据题意填写下表:
每小时走的路程(千米) 走完全程所用的时间(小时)
小明 x
小芳
⑵根据题意及表中所得到的信息列方程,求二人每小时各走几千米?
